斜率优化动态规划详解

问题描述：IOI2002 

    $N$个任务排成一个序列在一台机器上等待完成(顺序不得改变)，这$N$个任务被分成若干批，每批包含相邻的若干任务。从时刻0开始，这些任务被分批加工，第i个任务单独完成所需的时间是$T_{i}$。在每批任务开始前，机器需要启动时间S，而完成这批任务所需的时间是各个任务需要时间的总和（同一批任务将在同一时刻完成）。每个任务的费用是它的完成时刻乘以一个费用系数$C_{i}$。请确定一个分组方案，使得总费用最小。

思路解法1：

    利用区间分块的思想。
    设$F[i][j]$表示前i个任务分成j批加工需要的最小费用。那么我们只要枚举第j批，也就最后一批是从哪里开始做的就可以，第j批任务完成的时刻就是$j\times S+sumT[i]$,所以状态转移方程：$$F[i][j]=min\left \{ F[k][j-1]+(S\times j+sumT[i])\times(sumC[i]-sumC[k]) \right \},(0\leq k < i )$$

    这里：$$sumT[i]=\sum_{k=1}^{i}T_{k}$$ $$sumC[i]=\sum_{k=1}^{i}C_{k}$$  

    这样的做法比较普通和比较好想，但是时间复杂度比较高，达到了$O(N^3)$。

 

思路解法2：

    由于题目并没有强制规定要求分成几批来做，所以如果我们的状态里面不用出现j，那么我们就可以实现降维的目的。原先需要记录j是为了知道启动了几次，是为了计算完成任务的时间，那么我们新的状态设计必须在去掉j的情况下，也同样能够计算出完成任务的时间。
    我们知道如果当前这批任务开始执行了，那么这次启动的时间要影响接下来所有任务的完成时间，也就是接下来所有任务的完成时间都要因此推后$S$，所以我们可以计算每次启动对以后影响，这样就不需要直接记录启动的次数。
    设计状态F[i]表示前i个任务分若干批完成需要的最小代价，那么转移方程：

$$F[i]=min\left \{ F[j]+sumT[i]\times (sumC[i]-sumC[j])+S\times (sumC[n]-sumC[j]) \right \},(0\leq j<i)$$

 

思路解法3：
    如果N的范围比较小，前面两种解法，就足以能够在时限内出解。但是有没有更快的做法呢，在IOI2002年考的这题里面，N的范围高达30万，所以即使是N*N的算法也无法在1秒内出解。所以我们需要更加优化的算法。
    优化的方向在哪里呢，我们对j进行优化，解法2里面对j需要进行枚举。如果我们能够直接知道哪个j才是最优的，或者在均摊复杂度是O(1)的情况可以知道哪个j是最优的，那么这题的时间复杂度可以优化到O(n)，达到了算法理论时间复杂度的下界，已经是最优的解法了。
我们把算法2里面的转移方程略作整理，把不同类型的项尽量分开，方便我们来讨论：

$$F[i]=min\left \{ S\times sumC[n]+sumT[i]\times sumC[i]+F[j]-(S+sumT[i])\times sumC[j] \right \}$$

 

    明显的，我们可以发现在min函数里面的前面两项都是和如何选择j是没有关系的，在i确定的情况下，前面两项可以看成是一个常数，所以我们可以只比较最后一项的大小。

    于是:$$F[j]=sumC[j]\times (S+sumT[i])+P$$

$$P=F[i]-sumT[i]\times sumC[i]-S\times sumC[n]$$

    我们发现，这是一个一次函数，我们希望F[i]最小，就是希望截距P最小。我们可以用类似于数学里面线性规划的知识来解决,F[j]看成是y，sumC[j]看成是x。这些点已经存在在二维平面直接坐标系里面，而且过这些点的斜率也是确定的，如下图所示，我们可以得到最小的截距：

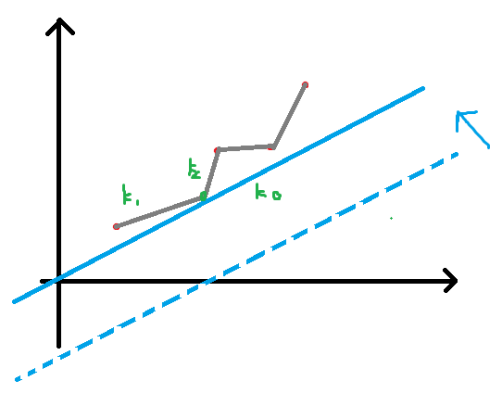
   我们发现，每次求解最小的截距，我们都是用这种平移的方法去找到第一个可以碰到的点。如果体现在数学计算上，我们可以看出这个碰到的点一定是凸包上的点。
   凸包（Convex Hull）是一个计算几何（图形学）中的概念。用不严谨的话来讲，给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边形，它能包含点集中所有的点。
   所以我们需要用一个队列来维护凸包上的点集，并且要求队首的两个点的斜率大于等于$S+sumT[i]$,对于每次求最小截距，队首的这个点一定就是我们需要点。
   由于每个点只进队一次，也只出队一次，所以每次求j的均摊时间复杂度就是$O(1)$，所以整个问题就在$O(N)$的时间内被解决了。