bzoj 4771: 七彩树

4771: 七彩树

Time Limit: 5 Sec  Memory Limit: 256 MB
Submit: 2104  Solved: 601
[Submit][Status][Discuss]

Description

给定一棵n个点的有根树，编号依次为1到n，其中1号点是根节点。每个节点都被染上了某一种颜色，其中第i个节

点的颜色为c[i]。如果c[i]=c[j]，那么我们认为点i和点j拥有相同的颜色。定义depth[i]为i节点与根节点的距离

，为了方便起见，你可以认为树上相邻的两个点之间的距离为1。站在这棵色彩斑斓的树前面，你将面临m个问题。

每个问题包含两个整数x和d，表示询问x子树里且depth不超过depth[x]+d的所有点中出现了多少种本质不同的颜色

。请写一个程序，快速回答这些询问。

 

Input

第一行包含一个正整数T(1<=T<=500)，表示测试数据的组数。

每组数据中，第一行包含两个正整数n(1<=n<=100000)和m(1<=m<=100000)，表示节点数和询问数。

第二行包含n个正整数，其中第i个数为c[i](1<=c[i]<=n)，分别表示每个节点的颜色。

第三行包含n-1个正整数，其中第i个数为f[i+1](1<=f[i]<i)，表示节点i+1的父亲节点的编号。

接下来m行，每行两个整数x(1<=x<=n)和d(0<=d<n)，依次表示每个询问。

输入数据经过了加密，对于每个询问，如果你读入了x和d，那么真实的x和d分别是x xor last和d xor last，

其中last表示这组数据中上一次询问的答案，如果这是当前数据的第一组询问，那么last=0。

输入数据保证n和m的总和不超过500000。

 

Output

对于每个询问输出一行一个整数，即答案。

 

Sample Input

1
5 8
1 3 3 2 2
1 1 3 3
1 0
0 0
3 0
1 3
2 1
2 0
6 2
4 1

Sample Output

1
2
3
1
1
2
1
1

HINT

 

思路：本题是dfs序+树链合并+set维护+主席树。

树链的并+STL-set+DFS序+可持久化线段树

如果没有深度限制，那么对于一种颜色，子树内包含该颜色的节点为：所有该颜色节点到根节点路径覆盖的所有节点，即树链的并。

因此对于每一种颜色求树链的并，支持链加操作；查询单个点的时候就是查询单点值。树上差分后转变为单点加、子树求和，使用DFS序转化为区间问题后使用数据结构维护。

那么有深度限制呢？我们按照深度维护可持久化线段树，第 $i$ 个版本我们只考虑深度小于等于 $i$ 的节点的影响。此时需要使用STL-set维护每个颜色的树链的并。

查询时直接查询depth[x]+d版本对应的可持久化线段树中，x节点子树内的权值和即可。

时间复杂度 $O(n\log n)$ 。

 

 

关于树链合并：

做法

按dfn序排好序后，
所有点到根距离-所有相邻两点lca到根距离为树链的并总长

sort(que+1,que+n+1,cmp);
for(i=1;i<=n;i++) res+=dis[que[i]];
for(i=1;i<=n;i++) res-=dis[LCA(que[i],que[i+1])];

简略证明

如图：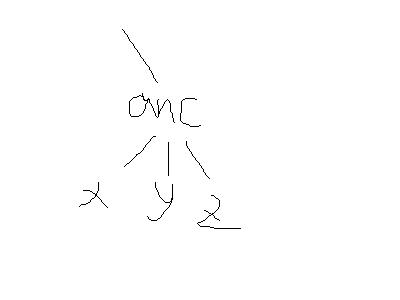

dfn序为anc,x,y,z
求x,y,z树链的并：dis[anc]加3次减2次
求x,y,z,anc树链的并：dis[anc]加4次减3次（LCA(anc,x)=anc）

用途

可以树链的并求和
也可以树链的并修改
可以解决子树不同数问题

 

#include<bits/stdc++.h>
using namespace std;  
#define R register int  
#define rep(i,a,b) for(R i=a;i<=b;i++) 
#define Rep(i,a,b) for(R i=a;i>=b;i--)  
#define mid        (l+r>>1) 
#define gc()       getchar()
#define ms(i,a)    memset(a,i,sizeof(a))    
template<class T>void read(T &x){
    x=0; char c=0; 
    while (!isdigit(c)) c=gc();  
    while (isdigit(c)) x=x*10+(c^48),c=gc();  
}
int const N=100000+3;
int n,m,rt[N],d[N],f[N][17],lc[N*40],rc[N*40],s[N*40],cnt,sum,tin[N],tout[N],tot,H[N],c[N],pos[N];   
set<int> se[N];  
set<int> :: iterator it;  
struct Edge{
    int to,nt; 
}E[N];  
struct node{
    int id,dp;  
    bool operator < (const node &rhs) const { return dp<rhs.dp;} 
}a[N];  
void add(int a,int b){
    E[++cnt]=(Edge){b,H[a]}; H[a]=cnt;
}
void dfs(int x,int fa){
    f[x][0]=fa;  
    d[x]=d[f[x][0]]+1; 
    tin[x]=++tot;  pos[tot]=x;  
    rep(j,1,16) f[x][j]=f[f[x][j-1]][j-1];  
    for(R i=H[x]; i; i=E[i].nt){
        int v=E[i].to;  
        dfs(v,x);  
    }
    tout[x]=tot;  
}      
void update(int old,int &x,int p,int l,int r,int v){
    x=++sum; lc[x]=lc[old]; rc[x]=rc[old]; s[x]=s[old]+v;  
    if(l==r) return ;  
    if(p<=mid) update(lc[old],lc[x],p,l,mid,v); 
    else update(rc[old],rc[x],p,mid+1,r,v); 
}
int lca(int x,int y){ 
    if(d[x]<d[y]) swap(x,y);  
    Rep(i,16,0) if((1<<i)<=d[x]-d[y]) x=f[x][i];  
    if(x==y) return x;  
    Rep(i,16,0) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];  
    return f[x][0]; 
}
int query(int x,int l,int r,int ll,int rr){
    if (!x) return 0; 
    if(ll<=l && r<=rr) return s[x];  
    int t1=0,t2=0;  
    if(ll<=mid) t1=query(lc[x],l,mid,ll,rr); 
    if(rr>mid)  t2=query(rc[x],mid+1,r,ll,rr);  
    return t1+t2;     
}

int main(){
    int T; read(T); 
    while (T--){
        read(n);  
        read(m);  
           cnt=tot=sum=0;  
           ms(0,H);ms(0,rt);    
           rep(i,1,n) read(c[i]); 
           rep(i,2,n) {
               int x; read(x);  
               add(x,i);  
           }
           dfs(1,0);   
           rep(i,1,n) a[i].id=i,a[i].dp=d[i];  
           sort(a+1,a+n+1);     
           rep(i,1,n) se[i].clear();   
           int p=1;       
           rep(i,1,n) {
               rt[i]=rt[i-1];   
               while (p<=n && a[p].dp<=i) {
                   update(rt[i],rt[i],tin[a[p].id],1,n,1);  
                   it=se[c[a[p].id]].lower_bound(tin[a[p].id]);  
                   int x=0,y=0;  
                   if(it!=se[c[a[p].id]].end()) x=pos[*it];  
                   if(it!=se[c[a[p].id]].begin())  y=pos[*(--it)];  
                   if(x) update(rt[i],rt[i],tin[lca(x,a[p].id)],1,n,-1);  
                   if(y) update(rt[i],rt[i],tin[lca(y,a[p].id)],1,n,-1);  
                   if(x && y) update(rt[i],rt[i],tin[lca(x,y)],1,n,1); 
                   se[c[a[p].id]].insert(tin[a[p].id]);   
                   p++; 
               } 
           }
           int last=0;    
           while (m--){
               int x,y; read(x); read(y);  
               x^=last; y=min(n,(y^last)+d[x]);  
               printf("%d\n",last=query(rt[y],1,n,tin[x],tout[x]) );  
           }
       }
       return 0; 
}