bzoj 1095 捉迷藏

Description

　　捉迷藏 Jiajia和Wind是一对恩爱的夫妻，并且他们有很多孩子。某天，Jiajia、Wind和孩子们决定在家里玩
捉迷藏游戏。他们的家很大且构造很奇特，由N个屋子和N-1条双向走廊组成，这N-1条走廊的分布使得任意两个屋
子都互相可达。游戏是这样进行的，孩子们负责躲藏，Jiajia负责找，而Wind负责操纵这N个屋子的灯。在起初的
时候，所有的灯都没有被打开。每一次，孩子们只会躲藏在没有开灯的房间中，但是为了增加刺激性，孩子们会要
求打开某个房间的电灯或者关闭某个房间的电灯。为了评估某一次游戏的复杂性，Jiajia希望知道可能的最远的两
个孩子的距离（即最远的两个关灯房间的距离）。我

将以如下形式定义每一种操作： C(hange) i 改变第i个房
间的照明状态，若原来打开，则关闭；若原来关闭，则打开。 G(ame) 开始一次游戏，查询最远的两个关灯房间的
距离。

Input

　　第一行包含一个整数N，表示房间的个数，房间将被编号为1,2,3…N的整数。接下来N-1行每行两个整数a, b，
表示房间a与房间b之间有一条走廊相连。接下来一行包含一个整数Q，表示操作次数。接着Q行，每行一个操作，如
上文所示。

Output

　　对于每一个操作Game，输出一个非负整数到hide.out，表示最远的两个关灯房间的距离。若只有一个房间是关
着灯的，输出0；若所有房间的灯都开着，输出-1。

Sample Input

8
1 2
2 3
3 4
3 5
3 6
6 7
6 8
7
G
C 1
G
C 2
G
C 1
G

Sample Output

4
3
3
4

HINT

对于100%的数据， N ≤100000, M ≤500000。

思路：本题有两种思路，传闻还有三种（第三种是边分治)

方法一：线段树，利用括号序列，很神奇的做法。

写个括号序列的做法。

首先dfs整棵树一遍，进入一个节点的时候加上一个左括号，然后是节点编号，当这个节点的所有子树遍历完后再添上一个右括号，这就是括号序列。（其实就是dfs序加上了括号而已）

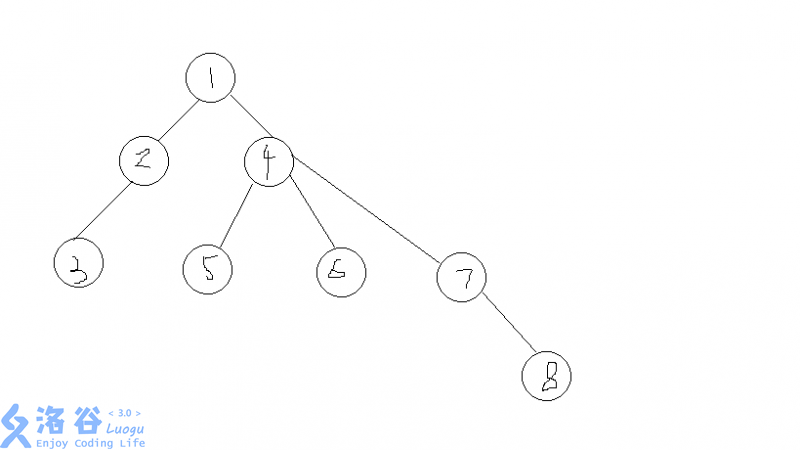
举个栗子，这棵树的括号序列是(1(2(3))(4(5)(6)(7(8))))

我们要求3到8的距离，截取两点间的括号序列为

3))(4(5)(6)(7(8

把编号和匹配的括号删掉

))(((

剩下了5个左右括号，而这就是3到8的距离。

这就是括号序列的性质。

怎么证明？脑补一下，到达i点时

1)添完了左右括号

那个点是i的祖先们的孩子。（不在i到根的路径上）

2）添了左括号没填右括号

那个点是i的祖先。（在i到根的路径上）

3）没添左括号

那个点是i的祖先们的孩子或者i的孩子（不在i到根的路径上）

因此，从s到t，删去的匹配括号们对于s来说是情况3，对于t来说是情况1，很显然这个点不在s到t的路径上。剩下的右括号，对于s来说是情况2，对于t来说是情况1，因此表示从s到达【t到根的这条链】经过的节点数。剩下的左括号，对于s来说是情况3，对于t来说是情况2，因此表示从t到达【s和t的lca（不包括lca）】的经过点数。

综上我们证明了删掉两点间所有匹配括号剩下的左右括号数为距离。

现在我们已经把整棵树压成了一个括号序列了，而我们要求的是两个黑点间的最大距离，我们考虑用线段树求解。

毫无疑问要记录每段区间删掉匹配括号后剩下的左右括号数，我们记右括号数为a，左括号数为b。

【注意我接下来说的所有左右区间都不限于线段树中的左右区间，任意连续的左右区间均可】

左右区间的a、b的合并：

显然左区间的左括号和右区间的右括号合并消去，谁多剩谁

 1 #include<bits/stdc++.h>
 2 using namespace std;  
 3 #define R register int
 4 #define rep(i,a,b) for(R i=a;i<=b;i++) 
 5 #define Rep(i,a,b) for(R i=a;i>=b;i--) 
 6 #define rp(i,x)    for(int i=H[x];i!=-1;i=E[i].nt)   
 7 #define ms(i,a)    memset(a,i,sizeof(a)) 
 8 #define gc()       getchar() 
 9 #define lc         (x<<1)
10 #define rc         (x<<1|1) 
11 #define mid        (l+r)/2  
12 template<class T>void read(T &x){
13   x=0; char c=0;  
14   while (!isdigit(c)) c=gc(); 
15   while (isdigit(c)) x=x*10+(c^48),c=gc();  
16 }
17 int const N=100001;  
18 int const M=500001;  
19 int const inf=1e9;  
20 int num,s[N*3],pos[N*10],H[N],n,m,cnt,tot,c[N];  
21 struct Edge{
22   int to,nt;  
23 }E[N<<1]; 
24 void add(int a,int b){
25   E[num]=(Edge){b,H[a]};H[a]=num++;  
26 }
27 struct node{
28   int a,b,l1,r1,l2,r2,dist;  
29 }t[N*3<<2];  
30 void dfs(int x,int fa){
31   s[++tot]=-1;s[++tot]=x; pos[x]=tot;  
32   rp(i,x){
33     int v=E[i].to;
34     if(v==fa) continue;  
35     dfs(v,x); 
36   }
37   s[++tot]=-2;  
38 }
39 void push(int x,int p){
40   t[x]=(node){0,0,-inf,-inf,-inf,-inf};  
41   if(s[p]==-1)  t[x].b=1; 
42   else if(s[p]==-2) t[x].a=1;  
43   else if(!c[s[p]]) t[x].l1=t[x].l2=t[x].r1=t[x].r2=0;  
44 }
45 void merge(int x){
46   if(t[lc].b>t[rc].a) t[x].a=t[lc].a,t[x].b=t[lc].b-t[rc].a+t[rc].b;  
47   else t[x].b=t[rc].b,t[x].a=t[lc].a+t[rc].a-t[lc].b;  
48   t[x].l1=max(t[lc].l1,max(t[rc].l1+t[lc].a-t[lc].b,t[rc].l2+t[lc].a+t[lc].b));
49   t[x].l2=max(t[lc].l2,t[rc].l2-t[lc].a+t[lc].b);
50   t[x].r1=max(t[rc].r1,max(t[lc].r1-t[rc].a+t[rc].b,t[lc].r2+t[rc].a+t[rc].b));
51   t[x].r2=max(t[rc].r2,t[lc].r2+t[rc].a-t[rc].b);
52   t[x].dist=max(max(t[lc].r1+t[rc].l2,t[lc].r2+t[rc].l1),max(t[lc].dist,t[rc].dist));
53 }
54 void build(int x,int l,int r){
55   if(l==r) { 
56     push(x,l); return ;
57   }
58   build(lc,l,mid); build(rc,mid+1,r);  
59   merge(x); 
60 }
61 void modify(int x,int l,int r,int p){
62   if(l==r) {
63     push(x,l); return ; 
64   }
65   if(p<=mid) modify(lc,l,mid,p); 
66   else modify(rc,mid+1,r,p);  
67   merge(x); 
68 } 
69 
70 int main(){
71   read(n);ms(-1,H);  
72   rep(i,1,n-1){
73     int x,y; read(x);read(y); 
74     add(x,y); add(y,x); 
75   }
76   dfs(1,0);  cnt=n ; 
77   build(1,1,tot);  
78   read(m);  
79   while (m--){
80     char s[2]; scanf("%s",s); 
81     if(s[0]=='C'){
82       int x; read(x);  
83       cnt+=c[x]? 1: -1; 
84       c[x]^=1;  
85       modify(1,1,tot,pos[x]); 
86     }else if(cnt==0) printf("-1\n");  
87     else if(cnt==1)  printf("0\n");  
88     else printf("%d\n",t[1].dist); 
89   }
90   return 0; 
91 }

View Code

思路2：动态点分治。

点分治的过程是对树块找重心之后分成多个小树块，降低规模分别处理的过程，把链的信息收到其中“最高重心”上，从所有的重心处像分治中的不同子树索取到重心的链，就可以覆盖所有链的信息。动态点分治就像把序列分治变成线段树一样，在分治的架子上加了信息维护，实现树链信息维护与查询。

需要什么？

每个重心需要其每个分离子树到它的信息（很重要，否则形成链的重复部分，并且还需要一个自己到自己的空信息维护单链上来的信息）

每个重心需要它到父分治块的信息

全局需要维护每个重心的信息

因此，考虑问题的静态版本，需要维护每个节点每个子树内的最长链，那么为了修改，最大化应换成堆维护。

每个重心维护一个堆，表示其分离子树中每个到它的最长链，c堆。

每个重心维护一个堆，表示其块内到父重心的每条链的长度，f堆。

全局维护一个堆，表示每个重心处的最长链，ans堆。

修改时只要从一个节点作为重心的块开始向上修改，就可以遍历到所有包含它的块，修改到父重心的信息，修改父重心的信息

注意开始时的节点的分离子树那个堆要插一个0表示单链，而改掉节点值的时候0的存在性也要相应地变化。

堆也比较有技巧：封装双堆分别为值和删了的值，取的时候两堆顶相同则pop，相当于变种删除标记

  1 #include <bits/stdc++.h>
  2 using namespace std;
  3 #define R register int
  4 #define rep(i, a, b) for (R i = a; i <= b; i++)
  5 #define Rep(i, a, b) for (R i = a; i >= b; i--)
  6 #define rp(i, x) for (R i = H[x]; i != -1; i = E[i].nt)
  7 #define ms(i, a) memset(a, i, sizeof(a))
  8 #define gc() getchar()
  9 #define LL long long
 10 template <class T>
 11 void read(T &x)
 12 {
 13     x = 0;
 14     char c = 0;
 15     while (!isdigit(c))
 16         c = gc();
 17     while (isdigit(c))
 18         x = x * 10 + (c ^ 48), c = gc();
 19 }
 20 int const N = 100003;
 21 int cnt, H[N], n, m, vis[N], mx, tg, s[N], sz, prt[N], d[N], fa[N][21], co[N], tin[N], tout[N], sum;
 22 struct Priority_queue
 23 {
 24     priority_queue<int> q, del;
 25     void push(int x) { q.push(x); }
 26     void erase(int x) { del.push(x); }
 27     int top()
 28     {
 29         while (del.size() && del.top() == q.top())
 30             del.pop(), q.pop();
 31         return q.top();
 32     }
 33     void pop()
 34     {
 35         while (del.size() && del.top() == q.top())
 36             del.pop(), q.pop();
 37         q.pop();
 38     }
 39     int sec_top()
 40     {
 41         int tmp = top();
 42         pop();
 43         int se = top();
 44         push(tmp);
 45         return se;
 46     }
 47     int size() { return q.size() - del.size(); }
 48 } c[N], f[N], ans;
 49 struct Edge
 50 {
 51     int to, nt;
 52 } E[N << 1];
 53 void add(int a, int b)
 54 {
 55     E[cnt] = (Edge){b, H[a]};
 56     H[a] = cnt++;
 57 }
 58 void dfs(int x, int p)
 59 {
 60     fa[x][0] = p;
 61     tin[x] = ++sum;
 62     rp(i, x)
 63     {
 64         int v = E[i].to;
 65         if (v == p)
 66             continue;
 67         d[v] = d[x] + 1;
 68         dfs(v, x);
 69     }
 70     tout[x] = ++sum;
 71 }
 72 
 73 void insert(Priority_queue &s)
 74 {
 75     if (s.size() > 1)
 76         ans.push(s.top() + s.sec_top());
 77 }
 78 void erase(Priority_queue &s)
 79 {
 80     if (s.size() > 1)
 81         ans.erase(s.top() + s.sec_top());
 82 }
 83 
 84 void init()
 85 {
 86     read(n);
 87     ms(-1, H);
 88     rep(i, 1, n - 1)
 89     {
 90         int x, y;
 91         read(x);
 92         read(y);
 93         add(x, y);
 94         add(y, x);
 95     }
 96     d[1] = 1;
 97     dfs(1, 1);
 98     rep(j, 1, 17) rep(i, 1, n) fa[i][j] = fa[fa[i][j - 1]][j - 1];
 99 }
100 
101 void dp(int x, int p)
102 {
103     s[x] = 1;
104     rp(i, x)
105     {
106         int v = E[i].to;
107         if (v == p || vis[v])
108             continue;
109         dp(v, x);
110         s[x] += s[v];
111     }
112 }
113 
114 void Biggest(int x, int p)
115 {
116     int num = 0;
117     rp(i, x)
118     {
119         int v = E[i].to;
120         if (v == p || vis[v])
121             continue;
122         Biggest(v, x);
123         num = max(num, s[v]);
124     }
125     if (mx > max(num, sz - s[x]))
126         mx = max(num, sz - s[x]), tg = x;
127 }
128 
129 int findroot(int x)
130 {
131     mx = n + 1;
132     tg = 0;
133     dp(x, 0);
134     sz = s[x];
135     Biggest(x, 0);
136     return tg;
137 }
138 
139 int inline ancestor(int x, int y)
140 {
141     return tin[x] <= tin[y] && tout[y] <= tout[x];
142 }
143 
144 int lca(int x, int y)
145 {
146     if (ancestor(x, y))
147         return x;
148     if (ancestor(y, x))
149         return y;
150     Rep(i, 17, 0) if (!ancestor(fa[x][i], y)) x = fa[x][i];
151     return fa[x][0];
152 }
153 int dist(int x, int y)
154 {
155     return d[x] + d[y] - 2 * d[lca(x, y)];
156 }
157 void work(int x, int p, int g)
158 {
159     f[g].push(dist(x, prt[g]));
160     rp(i, x)
161     {
162         int v = E[i].to;
163         if (v == p || vis[v])
164             continue;
165         work(v, x, g);
166     }
167 }
168 int Div(int x, int p)
169 {
170     int g = findroot(x);
171     prt[g] = p;
172     work(g, 0, g);
173     vis[g] = 1;
174     c[g].push(0);
175     rp(i, g)
176     {
177         int v = E[i].to;
178         if (vis[v])
179             continue;
180         int gg = Div(v, g);
181         c[g].push(f[gg].top());
182     }
183     insert(c[g]);
184     return g;
185 }
186 void light(int x)
187 {
188     erase(c[x]);
189     c[x].erase(0);
190     insert(c[x]);
191     for (int k = x; prt[k]; k = prt[k])
192     {
193         erase(c[prt[k]]);
194         if (f[k].size())
195             c[prt[k]].erase(f[k].top());
196         f[k].erase(dist(x, prt[k]));
197         if (f[k].size())
198             c[prt[k]].push(f[k].top());
199         insert(c[prt[k]]); 
200     }
201 }
202 void weight(int x)
203 {
204     erase(c[x]);
205     c[x].push(0);
206     insert(c[x]);
207     for (int k = x; prt[k]; k = prt[k])
208     {
209         erase(c[prt[k]]);
210         if (f[k].size())
211             c[prt[k]].erase(f[k].top());
212         f[k].push(dist(x, prt[k]));
213         if (f[k].size())
214             c[prt[k]].push(f[k].top());
215         insert(c[prt[k]]);
216     }
217 }
218 void solve()
219 {
220     cnt = n;
221     read(m);
222     while (m--)
223     {
224         char ch[5];
225         scanf("%s", ch);
226         if (ch[0] == 'G')
227         {
228             if (cnt == 1)
229                 printf("%d\n", cnt - 1);
230             else
231                 printf("%d\n", ans.top());
232         }
233         else
234         {
235             int x;
236             read(x);
237             if (!co[x])
238                 cnt--, light(x);
239             else
240                 cnt++, weight(x);
241             co[x] ^= 1;
242         }
243     }
244 }
245 
246 int main()
247 {
248     init();
249     Div(1, 0);
250     solve();
251     return 0;
252 }