luogu4219 and bzoj4530 大融合
题目描述
小强要在NN个孤立的星球上建立起一套通信系统。这套通信系统就是连接NN个点的一个树。 这个树的边是一条一条添加上去的。在某个时刻,一条边的负载就是它所在的当前能够 联通的树上路过它的简单路径的数量。
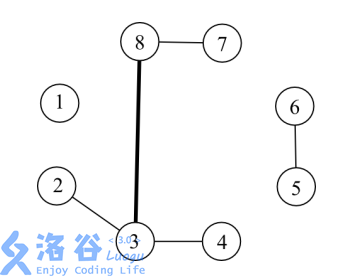
例如,在上图中,现在一共有了55条边。其中,(3,8)(3,8)这条边的负载是66,因 为有六条简单路径2-3-82−3−8,2-3-8-72−3−8−7,3-8,3-8-73−8,3−8−7,4-3-84−3−8,4-3-8-74−3−8−7路过了(3,8)(3,8)。
现在,你的任务就是随着边的添加,动态的回答小强对于某些边的负载的 询问。
输入输出格式
输入格式:
第一行包含两个整数 N, QN,Q,表示星球的数量和操作的数量。星球从 11 开始编号。
接下来的 QQ 行,每行是如下两种格式之一:
A x y表示在 xx和 yy 之间连一条边。保证之前 xx 和 yy是不联通的。Q x y表示询问 (x,y)(x,y) 这条边上的负载。保证 xx 和 yy 之间有一条边。
输出格式:
对每个查询操作,输出被查询的边的负载。
输入输出样例
说明
对于所有数据,1≤N,Q≤10^51≤N,Q≤105
本题可以树链剖分+并查集,先把树建好,然后每次加边x和y,假设x的深度小,那么我们通过并查集求出与x连接的最早的祖先。维护x到最早的祖先这个链(每个点加上y子树的点的个数)。

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define re register 4 #define R re int 5 #define rep(i,a,b) for(R i=a;i<=b;i++) 6 #define Rep(i,a,b) for(R i=a;i>=b;i--) 7 #define ms(i,a) memset(a,i,sizeof(a)) 8 #define V inline void 9 #define I inline int 10 #define lc (x<<1) 11 #define rc (x<<1|1) 12 #define mid ((l+r)>>1) 13 template<class T>V read(T &x){ 14 x=0;char c=getchar(); 15 while (!isdigit(c)) c=getchar(); 16 while (isdigit(c)) x=x*10+(c^48),c=getchar(); 17 } 18 template<class T>void write(T x){if(x>9) write(x/10);putchar(48+x%10);} 19 int const maxn=100001; 20 struct Edge{int to,nt;}E[maxn<<1]; 21 struct Q{int x,y,z;}q[maxn]; 22 int n,m,top[maxn],id[maxn],f[maxn],sz[maxn],son[maxn],cnt,sum,H[maxn],dep[maxn],g[maxn]; 23 struct SegT{ 24 int tg[maxn<<2],num[maxn<<2]; 25 void build(int x,int l,int r){ 26 if(l==r) {num[x]=1;return; } 27 build(lc,l,mid); build(rc,mid+1,r); 28 } 29 void pushd(int x){ 30 tg[lc]+=tg[x]; tg[rc]+=tg[x]; tg[x]=0; 31 } 32 void update(int x,int l,int r,int ll,int rr,int v){ 33 if(l==ll && r==rr){ tg[x]+=v; return; } 34 if(rr<=mid) update(lc,l,mid,ll,rr,v); 35 else if(ll>mid) update(rc,mid+1,r,ll,rr,v); 36 else update(lc,l,mid,ll,mid,v),update(rc,mid+1,r,mid+1,rr,v); 37 } 38 int query(int x,int l,int r,int p){ 39 if(l==r) return num[x]+tg[x]; 40 pushd(x) ; 41 if(p<=mid) return query(lc,l,mid,p); 42 else return query(rc,mid+1,r,p); 43 } 44 }T; 45 void add(int a,int b){ 46 E[cnt]=(Edge){b,H[a]};H[a]=cnt++; 47 E[cnt]=(Edge){a,H[b]};H[b]=cnt++; 48 } 49 int gf(int x){return x==g[x]? x:g[x]=gf(g[x]); } 50 void dfs1(int x,int fa){ 51 sz[x]=1; dep[x]=dep[fa]+1; f[x]=fa; 52 for(R i=H[x];i!=-1;i=E[i].nt){ 53 int v=E[i].to; 54 if(v==fa) continue; 55 dfs1(v,x); 56 if(sz[son[x]]<sz[v]) son[x]=v; 57 sz[x]+=sz[v]; 58 } 59 } 60 void dfs2(int x,int fa,int tp){ 61 top[x]=tp; id[x]=++sum; 62 if(son[x]) dfs2(son[x],x,tp); 63 for(R i=H[x];i!=-1;i=E[i].nt){ 64 int v=E[i].to; 65 if(v==fa || v==son[x]) continue; 66 dfs2(v,x,v); 67 } 68 } 69 void modify(int x,int y,int v){ 70 while(top[x]^top[y]){ 71 if(dep[top[x]]<dep[top[y]]) swap(x,y); 72 int tx=top[x]; 73 T.update(1,1,n,id[tx],id[x],v); 74 x=f[tx]; 75 } 76 if(dep[x]<dep[y]) swap(x,y); 77 T.update(1,1,n,id[y],id[x],v); 78 } 79 int main(){ 80 scanf("%d%d",&n,&m);ms(-1,H); 81 rep(i,1,m){ 82 char s[2]; scanf("%s",s); scanf("%d%d",&q[i].x,&q[i].y); 83 if(s[0]=='A') q[i].z=1,add(q[i].x,q[i].y); 84 } 85 rep(i,1,n) if(!sz[i]) dfs1(i,i); 86 rep(i,1,n) if(!id[i]) dfs2(i,i,i); 87 T.build(1,1,n); 88 rep(i,1,n) g[i]=i; 89 rep(i,1,m){ 90 if(dep[q[i].x]> dep[q[i].y]) swap(q[i].x,q[i].y); 91 int x=gf(q[i].x),y=q[i].y; 92 if(q[i].z==1){ 93 int t=T.query(1,1,n,id[y]); 94 modify(x,q[i].x,t); g[y]=x; 95 }else { 96 int t1=T.query(1,1,n,id[y]); 97 int t2=T.query(1,1,n,id[x]); 98 printf("%d\n",t1*(t2-t1)); 99 } 100 } 101 return 0; 102 }
此题也可以直接lct,维护子树信息即可。
LCT维护子树信息
学了大神的LCT维护子树信息的方式,觉得还算好理解,于是自己yy了这道题。
我们知道,在LCT中的Splay Tree中,access某个点并splay到根,那么它的实儿子记录的信息是这条链的信息,并不是我们想要的子树信息。
而所有实儿子和虚儿子的信息才是我们想要求的子树信息。
但是由于虚儿子“儿子认爹,爹不认儿子”的性质,无法在pushup的时候上传信息。
事实上,我们注意到,对于Splay Tree的所有基本操作,除了access和link以外,都不会对虚儿子的信息进行修改。
那么我们每次在添加虚儿子时,顺便把虚儿子的信息也记录到父亲节点中。
这样我们每次调用一个节点时,将它Splay Tree中实儿子的信息,加上它自身的虚儿子的信息,就是我们想要的子树信息。
于是我们对于每个节点记录两个信息:它的总信息和它虚儿子的信息,pushup时更新x的总信息为:x实儿子的总信息+x虚儿子的信息+x本身的信息。
按照这种方法我们来思考这道题,可以发现所求的答案就是一条边两端点的子树大小乘积,我们把某一个端点定为整棵树的根,可以知道整棵树的大小,而根据另一个节点可以知道一个子树的大小,相减即为另一个子树的大小。
具体的实现:
access操作中割断了实边c[1][x],该边变为了虚边,所以应该加到x的虚儿子信息中,加入了实边t,该边不再是虚边,所以应从x的虚儿子信息中减去。
link操作中为了在加入x时同时更新y的信息,需要makeroot(x),makeroot(y),然后连x->y的虚边(实际上只需要access(y)和splay(y))。
其余的操作,和普通的LCT没有任何区别。
代码中需要注意的是,sum[x]存的是总信息(子树大小),si[x]存的是虚儿子信息(子树除了链以外的大小),不要弄混。

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define re register 4 #define R re int 5 #define rep(i,a,b) for(R i=a;i<=b;i++) 6 #define Rep(i,a,b) for(R i=a;i>=b;i--) 7 #define ms(i,a) memset(a,i,sizeof(a)) 8 #define lc ch[x][0] 9 #define rc ch[x][1] 10 #define pa fa[x] 11 #define I inline int 12 template<class T>I read(T &x){ 13 x=0; char c=0; 14 while (!isdigit(c)) c=getchar(); 15 while (isdigit(c)) x=x*10+(c^48),c=getchar(); 16 } 17 int const maxn=100001; 18 int st[maxn],n,m,top; 19 struct Lct{ 20 int ch[maxn][2],s[maxn],si[maxn],r[maxn],fa[maxn]; 21 I get(int x){return ch[pa][1]==x;} 22 I isr(int x){return ch[pa][0]!=x && ch[pa][1]!=x;} 23 I update(int x){ s[x]=s[lc]+s[rc]+si[x]+1;} 24 I pushd(int x){ 25 if(!r[x]) return 0; 26 swap(ch[lc][0],ch[lc][1]); 27 swap(ch[rc][0],ch[rc][1]); 28 r[lc]^=1;r[rc]^=1;r[x]=0; 29 } 30 I con(int x,int y,int z){fa[x]=y; ch[y][z]=x;} 31 I rotate(int x){ 32 int f=fa[x],g=fa[f],c=get(x),cc=get(f); 33 if(!isr(f)) ch[g][cc]=x; fa[x]=g; 34 con(ch[x][c^1],f,c); con(f,x,c^1); 35 update(f); update(x); 36 } 37 I splay(int x){ 38 top=0; int k=x; while (!isr(k)) st[++top]=k,k=fa[k];st[++top]=k; 39 while (top) pushd(st[top--]); 40 for(; !isr(x); rotate(x)) if(!isr(pa)) rotate(get(x)==get(pa)? pa:x); 41 } 42 I access(int x){ 43 for(int y=0;x ;y=x,x=pa){ 44 splay(x); si[x]+=s[rc]; si[x]-=s[rc=y]; update(x); 45 } 46 } 47 I make(int x){access(x); splay(x); r[x]^=1; swap(lc,rc);} 48 I find(int x){access(x); splay(x); while (lc) x=lc; return x;} 49 I split(int x,int y){make(x); access(y); splay(y); } 50 I link(int x,int y){ 51 split(x,y);si[fa[x]=y]+=s[x]; update(y); 52 } 53 }lct; 54 int main(){ 55 read(n); read(m); 56 while (m--){ 57 char s[2]; int x,y; 58 scanf("%s",s); read(x); read(y); 59 if(s[0]=='A') lct.link(x,y); 60 else { 61 lct.split(x,y); 62 printf("%d\n",(lct.si[x]+1)*(lct.si[y]+1)); 63 } 64 } 65 return 0; 66 }




