大佬的lct讲解（转)

博客太长啦！于是将重要的部分留在题解中，LCT的概念、三个基本性质等更多内容可以参考博客LCT总结（未完结，持续更新中！）

LCT核心操作，也是最难理解的操作。其它所有的操作都是在此基础上完成的。

因为性质3，我们不能总是保证两个点之间的路径是直接连通的（在一条Splay上）。

access即定义为打通根节点到指定节点的路径。

~~蒟蒻深知没图的痛苦QwQ~~ 所以还是来几张ppt图吧。

下面的图片参考YangZhe的论文

有一棵树，假设一开始轻边和重边是这样划分的（虚线为轻边）

那么所构成的LCT可能会长这样（绿框中为一个Splay，可能不会长这样，但只要满足中序遍历按深度递增（性质1）就对结果无影响）

现在我们要

因为性质2，该路径上其它链都要给这条链让路，也就是把每个点到该路径以外的重边变轻。

所以我们希望轻重边重新划分成这样。

然后怎么实现呢？我们要一步步往上拉。

首先把

为了满足性质2，原来

因为按深度

然后就变成了这样——

我们接着把

原来在

这时候

然后就变成了这样——

代码其实很简单。。。。。。循环处理，只有四步——

转到根；
换儿子；
更新信息；
当前操作点切换为轻边所指的父亲，转1

inline void access(int x){
    for(int y=0;x;y=x,x=f[x])
        splay(x),c[x][1]=y,pushup(x);//儿子变了，需要及时上传信息
}

只是把根到某个节点的路径拉起来并不能满足我们的需要。更多时候，我们要获取指定两个节点之间的路径信息。

然而一定会出现路径不能满足按深度严格递增的要求的情况。根据性质1，这样的路径不能在一个Splay中。

Then what can we do?

这时候就利用到

代码

inline void pushr(int x){//Splay区间翻转操作
    swap(c[x][0],c[x][1]);
    r[x]^=1;//r为区间翻转懒标记数组
}
inline void makeroot(int x){
    access(x);splay(x);
    pushr(x);
}

关于pushdown和makeroot的一个相关的小问题详见下方update（关于pushdown的说明）

找

代码：

inline int findroot(R x){
    access(x); splay(x);
    while(c[x][0])pushdown(x),x=c[x][0];
//如要获得正确的原树树根，一定pushdown！详见下方update（关于findroot中pushdown的说明）
    splay(x);//此处的问题详见下方update（关于findroot中splay(x)的说明）
    return x;
}

同样利用性质1，不停找左儿子，因为其深度一定比当前点深度小。

神奇的

split(x,y)定义为拉出

代码

inline void split(int x,int y){
    makeroot(x);
    access(y);splay(y);
}

x成为了根，那么x到y的路径就可以用

连一条

代码

inline bool link(int x,int y){
    makeroot(x);
    if(findroot(y)==x)return 0;//两点已经在同一子树中，再连边不合法
    f[x]=y;
    return 1;
}

如果题目保证连边合法，代码就可以更简单

inline void link(int x,int y){
    makeroot(x);
    f[x]=y;
}

将

如果题目保证断边合法，倒是很方便。

使

inline void cut(int x,int y){
    split(x,y);
    f[x]=c[y][0]=0;
    pushup(y);//少了个儿子，也要上传一下
}

那如果不一定存在该边呢？

充分利用好Splay和LCT的各种基本性质吧！

正确姿势——先判一下连通性，再看看

因为

那么可能

也可能

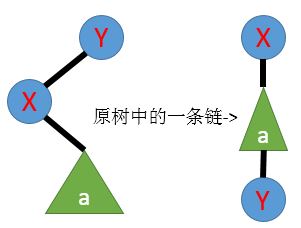
只有三个条件都满足，才可以断掉。

inline bool cut(int x,int y){
    makeroot(x);
    if(findroot(y)!=x||f[x]!=y||c[x][1])return 0;
    f[x]=c[y][0]=0;
    pushup(y);
    return 1;
}

如果维护了

inline bool cut(int x,int y){
    makeroot(x);
    if(findroot(y)!=x||sz[y]>2)return 0;
    f[x]=c[y][0]=0;
    pushup(y);
}

解释一下，如果他们有直接连边的话，

反过来说，如果有其它的点，

其实，还有一些LCT中的Splay的操作，跟我们以往学习的纯Splay的某些操作细节不甚相同。

包括

#include<cstdio>
#include<cstdlib>
#define R register int
#define I inline void
#define lc c[x][0]
#define rc c[x][1]
#define G ch=getchar()
#define in(z) G;\
    while(ch<'-')G;\
    z=ch&15;G;\
    while(ch>'-')z*=10,z+=ch&15,G;
const int N=300009;
int f[N],c[N][2],v[N],s[N],st[N];
bool r[N];
inline bool nroot(R x){//判断节点是否为一个Splay的根（与普通Splay的区别1）
    return c[f[x]][0]==x||c[f[x]][1]==x;
}//原理很简单，如果连的是轻边，他的父亲的儿子里没有它
I pushup(R x){//上传信息
    s[x]=s[lc]^s[rc]^v[x];
}
I pushr(R x){R t=lc;lc=rc;rc=t;r[x]^=1;}//翻转操作
I pushdown(R x){//判断并释放懒标记
    if(r[x]){
        if(lc)pushr(lc);
        if(rc)pushr(rc);
        r[x]=0;
    }
}
I rotate(R x){//一次旋转
    R y=f[x],z=f[y],k=c[y][1]==x,w=c[x][!k];
    if(nroot(y))c[z][c[z][1]==y]=x;c[x][!k]=y;c[y][k]=w;//额外注意if(nroot(y))语句，此处不判断会引起致命错误（与普通Splay的区别2）
    if(w)f[w]=y;f[y]=x;f[x]=z;
    pushup(y);
}
I splay(R x){//只传了一个参数，因为所有操作的目标都是该Splay的根（与普通Splay的区别3）
    R y=x,z=0;
    st[++z]=y;//st为栈，暂存当前点到根的整条路径，pushdown时一定要从上往下放标记（与普通Splay的区别4）
    while(nroot(y))st[++z]=y=f[y];
    while(z)pushdown(st[z--]);
/*当然了，其实利用函数堆栈也很方便，代替上面几行手动栈，就像这样
I pushall(R x){
    if(nroot(x))pushall(f[x]);
    pushdown(x);
}*/
    while(nroot(x)){
        y=f[x];z=f[y];
        if(nroot(y))
            rotate((c[y][0]==x)^(c[z][0]==y)?x:y);
        rotate(x);
    }
    pushup(x);
}
I access(R x){//访问
    for(R y=0;x;x=f[y=x])
        splay(x),rc=y,pushup(x);
}
I makeroot(R x){//换根
    access(x);splay(x);
    pushr(x);
}
inline int findroot(R x){//找根（在真实的树中的）
    access(x);splay(x);
    while(lc)pushdown(x),x=lc;
    //splay(x);（在本模板中建议不写）
    return x;
}
I split(R x,R y){//提取路径
    makeroot(x);
    access(y);splay(y);
}
I link(R x,R y){//连边
    makeroot(x);
    if(findroot(y)!=x)f[x]=y;
}
I cut(R x,R y){//断边
    makeroot(x);
    if(findroot(y)==x&&f[x]==y&&!rc){
        f[x]=c[y][0]=0;
        pushup(y);
    }
}
int main()
{
    register char ch;
    R n,m,i,type,x,y;
    in(n);in(m);
    for(i=1;i<=n;++i){in(v[i]);}
    while(m--){
        in(type);in(x);in(y);
        switch(type){
        case 0:split(x,y);printf("%d\n",s[y]);break;
        case 1:link(x,y);break;
        case 2:cut(x,y);break;
        case 3:splay(x);v[x]=y;//先把x转上去再改，不然会影响Splay信息的正确性
        }
    }
    return 0;
}

update（关于findroot中pushdown的说明）

蒟蒻真的一时没注意这个问题。。。。。。Splay根本没学好

找根的时候，当然不能保证Splay中到根的路径上的翻转标记全放掉。

所以最好把pushdown写上。

在本题中不写pushdown不会出问题（证明很困难，大概是因为子树结构会保持相对稳定而找到的点即使是错的但也是一样的？）

Candy巨佬的总结对pushdown问题有详细的分析

只不过蒟蒻后来经常习惯这样判连通性（~~我也不知道怎么养成的~~）

makeroot(x);
if(findroot(y)==x)//后续省略

这样好像没出过问题，那应该可以证明是没问题的（makeroot保证了x在LCT的顶端，access(y)+splay(y)以后，假如x,y在一个Splay里，那x到y的路径一定全部放完了标记）

导致很久没有发现错误。。。。。。

另外提一下，假如LCT题目在维护连通性的情况中只可能出现合并而不会出现分离的话，其实可以用并查集哦！（实践证明findroot很慢）

这样的例子有不少，比如下面“维护链上的边权信息”部分的两道题都是的。

甚至听到Julao们说有少量题目还专门卡这个细节。。。。。。XZY巨佬的博客就提到了（~~我太弱啦，暂时并不会~~）

update（关于pushdown的说明）

我pushdown和makeroot有时候会这样写，常数小一点

void pushdown(int x){
    if(r[x]){
        r[x]=0;
        int t=c[x][0];
        r[c[x][0]=c[x][1]]^=1;
        r[c[x][1]=t]^=1;
    }
}
void makeroot(int x){
    access(x);splay(x);
    r[x]^=1;
}

这种写法等于说当x有懒标记时，x的左右儿子还是反的

~~那么如果findroot里实在要写pushdown，那么这种pushdown就会出现问题~~（参考cnblogs评论区@ zjp_shadow巨佬的指正）

再次update，蒟蒻发现这种问题还是可以避免的，若用这种pushdown，findroot可以写，这样写就好啦

inline int findroot(int x){
    access(x);splay(x);
    pushdown(x);
    while(lc)pushdown(x=lc);
    splay(x);
    return x;
}

所以此总结以及下面模板里的pushdown，常数大了一点点，却是更稳妥、严谨的写法

//pushr同上方makeroot部分
void pushdown(int x){
    if(r[x]){
        if(c[x][0])pushr(c[x][0]);//copy自模板，然后发现if可以不写
        if(c[x][1])pushr(c[x][1]);
        r[x]=0;
    }
}
void makeroot(int x){
    access(x);splay(x);
    pushr(x);//可以看到两种写法造成makeroot都是不一样的
}

这种写法等于说当x有懒标记时，x的左右儿子已经放到正确的位置了，只是儿子的儿子还是反的

那么这样就不会出问题啦

两种写法差别还确实有点大呢

有些Splay题目的pushdown如果用这种不严谨写法会是错的，比如[NOI2005]维护数列

update（关于findroot中splay(x)的说明）

某位Julao指出findroot中在找到原树根后（此时x跳到了原树根）应splay(x)，伸展一下，Splay的特性，保证复杂度(好像牵涉到玄学的势能分析，蒟蒻什么也不会啊QvQ)

非常正确的做法。于是本蒟蒻进行了更正，却忘记了进行验证。

后来Destinies巨佬指出第8个点WA。

经过验证之后发现，加上splay(x)以后，点的相对位置发生了变化，导致cut需要更改，更改如下：

I cut(R x,R y){//断边
    makeroot(x);
    if(findroot(y)==x&&f[y]==x&&!c[y][0]){
        f[y]=c[x][1]=0;//x在findroot(y)后被转到了根
        pushup(x);
    }
}

为了避免频繁讨论、修改带来的繁琐，此总结不建议在此模板题里加上splay(x)

因为确实很难找到卡掉不写splay(x)的代码的数据，而且可能带来一点常数。

或许我大多数时候把splay写成单旋（没错就是HNOI2017那种）会比Zig、Zag双旋要快个十几分之一也是这样的道理吧。。。。。。

但这不意味着就不用写了

在比较关键的时候（比如比赛时）该写的总要写。

不管是单旋，还是不splay(x)，都是很容易卡掉的。。。。。。

相信Dalao们都能熟练地在很多种不同的写法中切换的

posted @ 2018-11-27 16:29 zjxxcn 阅读(745) 评论(0) 编辑收藏举报

刷新页面返回顶部

zjxxcn

大佬的lct讲解（转)

access(x)access(x)

makeroot(x)makeroot(x)

findroot(x)findroot(x)

split(x,y)split(x,y)

link(x,y)link(x,y)

cut(x,y)cut(x,y)

update（关于findroot中pushdown的说明）

update（关于pushdown的说明）

update（关于findroot中splay(x)的说明）

公告