100层楼两部手机，找出至少需要扔多少次能找到恰好能保证手机不被摔碎的楼层

100层楼两部手机，找出至少需要扔多少次能找到恰好能保证手机不被摔碎的楼层

前言

​ 前不久遇到一个人问我这个问题，大概是这样的：你现在有两部手机，然后有一栋100层楼高的楼层，最少需要扔多少次手机，你才能找到恰好能保证手机不被摔碎的楼层？手机一旦摔碎就无法再继续测试了，我们会至少从1层扔，0层一定不会碎（即有100层楼可以给我们选择）

​ 当时一下就白给了，后面想了下发现其实也不是很难，下面讲一下我最近想到的该如何去寻找这个值。

思路

​ 我们总共只有2部手机，假如我们第一次选择的楼层为x，如果此时第一部手机摔碎了，剩下的(x - 1)层楼我们必须从1楼开始扔，扔到第(x-1)层，才能知道哪一层恰好可以保证手机不被摔碎，那么总共就需要x次是吧；与此同时，如果此时在x层我们没有摔碎手机，那我们可以再往上找一个新的楼层开始扔，我们假设为x2吧，那么如果此时手机摔碎了，我们要从第(x + 1)层开始往上找到第(x2 - 1)层，才能找到恰好能保证手机不被摔碎的楼层。大概思路是这样，那我们先随便找个方式试一下吧。

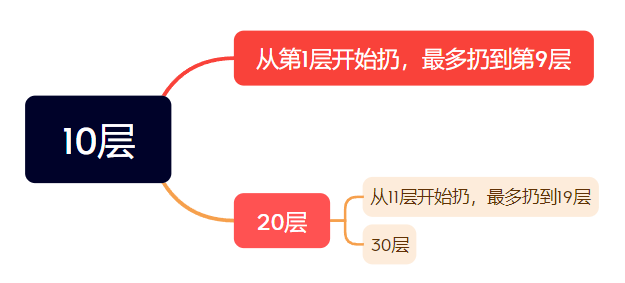
​ 假设我们每10层扔一次，假如第一次扔摔碎了，我们从1楼开始扔，最多扔到9层就可以找到在1-9楼哪个楼层恰好不碎了，加上我们一开始在10楼扔了一次，我们最多需要扔10次就可以找到答案了；如果第一次没摔碎，我们从第20层开始扔，假如第二次扔摔碎了，我们从第11楼开始扔，从11楼找到第19楼同样需要9次，加上在第10楼与第20楼扔的两次，总共需要11次。这时候我们就发现问题了：

​ 如果我们每10楼一扔，那么在越高的楼层才恰好会碎的话，我们需要的次数越多！每当我们扔了一次后，就应该让在下一次会扔碎的楼层最大需要查找的次数减一，从而使其达到一种平衡，即不管它在我们第几次仍的时候碎掉了，其最坏情况时所需要的查找次数相等

​ 假设我们在第x层开始扔，为了保证下次扔的时候，最坏情况与第一次扔就碎的最大所需次数相等，那我们第二次就应该在第x + x - 1层扔，这样我们就能保证如果第二次扔的时候坏了，也同样需要x次就可以找到目标楼层。依次类推，最后一次扔的时候只需要查找一次即可。

可得到如下式子：x + (x - 1) + ... + 2 + 1 >= 100，使用等差求和公式与简单的一元二次方程的知识，就可以轻松得到x>=14，即最多我们需要14次就可以找到答案！