【知识强化】第五章 图 5.2 图的存储及基本操作
上节课我们学习了有关图的逻辑结构,图的定义以及相关重要的基本概念。本节课我们来接触图的基本结构。图是如何进行存储的呢?今天学习的方法就是邻接矩阵法。

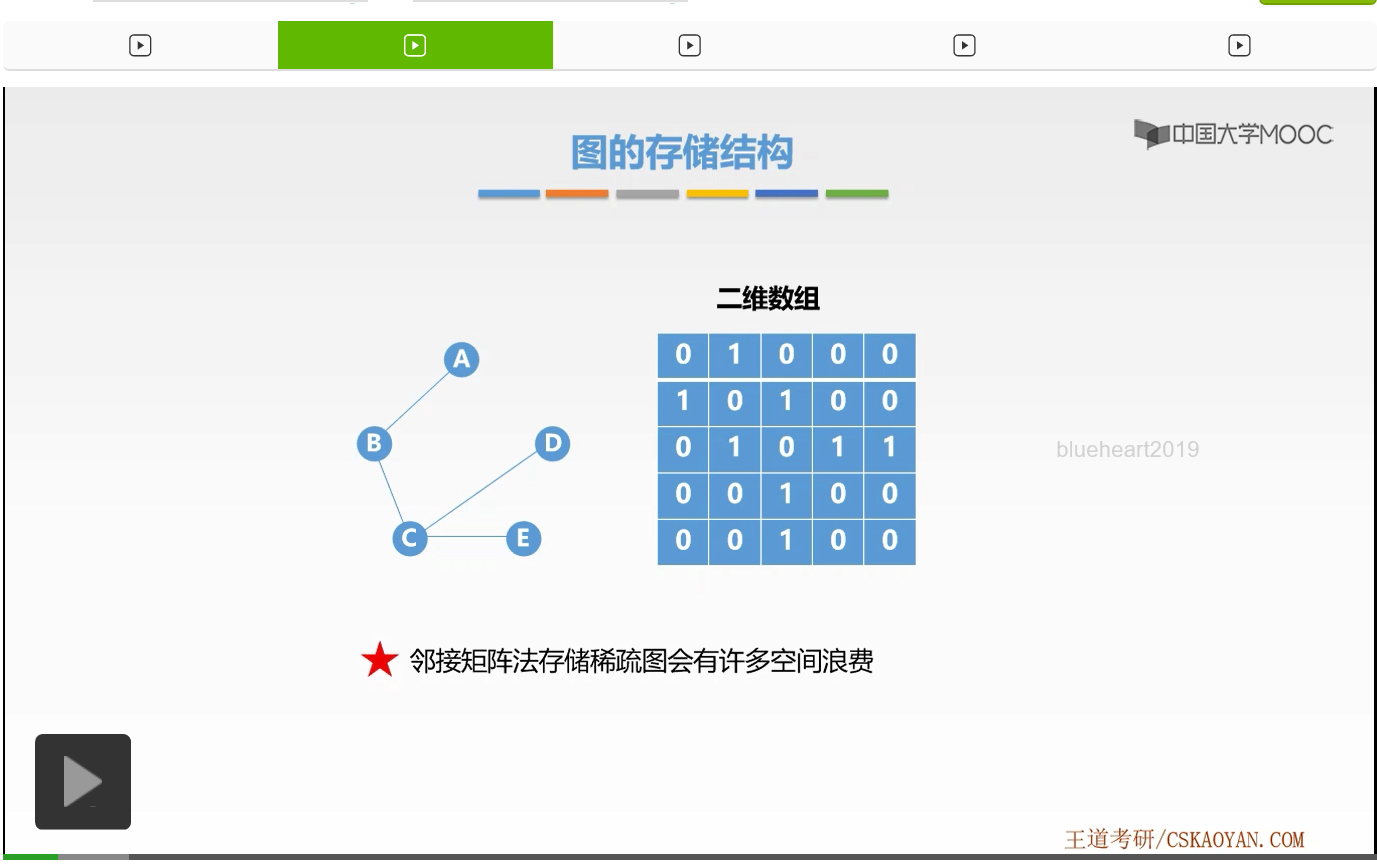
什么是邻接矩阵法,我们来看这样一个例子。这是一个无向图,那么上一节课我们讲述过怎样表示该图呢?如果该图是G的话,我们有两个集合。第一个是点集V,它保存了所有结点。第二个是边集E,它保存了结点之间的关系也就是我们所说的边。那么我们存储该图是不是就是存储该点集合该边集啊。怎样存储呢?在邻接矩阵法当中我们用一个一维数组来存放了每一个结点。而用一个二维数组来存放了每一条边。怎样存放呢?怎样存放呢?其实就是它是一种其实它是一种矩阵的形式。那么其中行号表示了这个边的起始端点,列号表示它的终止端点,而其中的值表示的是该边是否存在以及该边的一些权重。这就是一个二维数组表示边的方法。
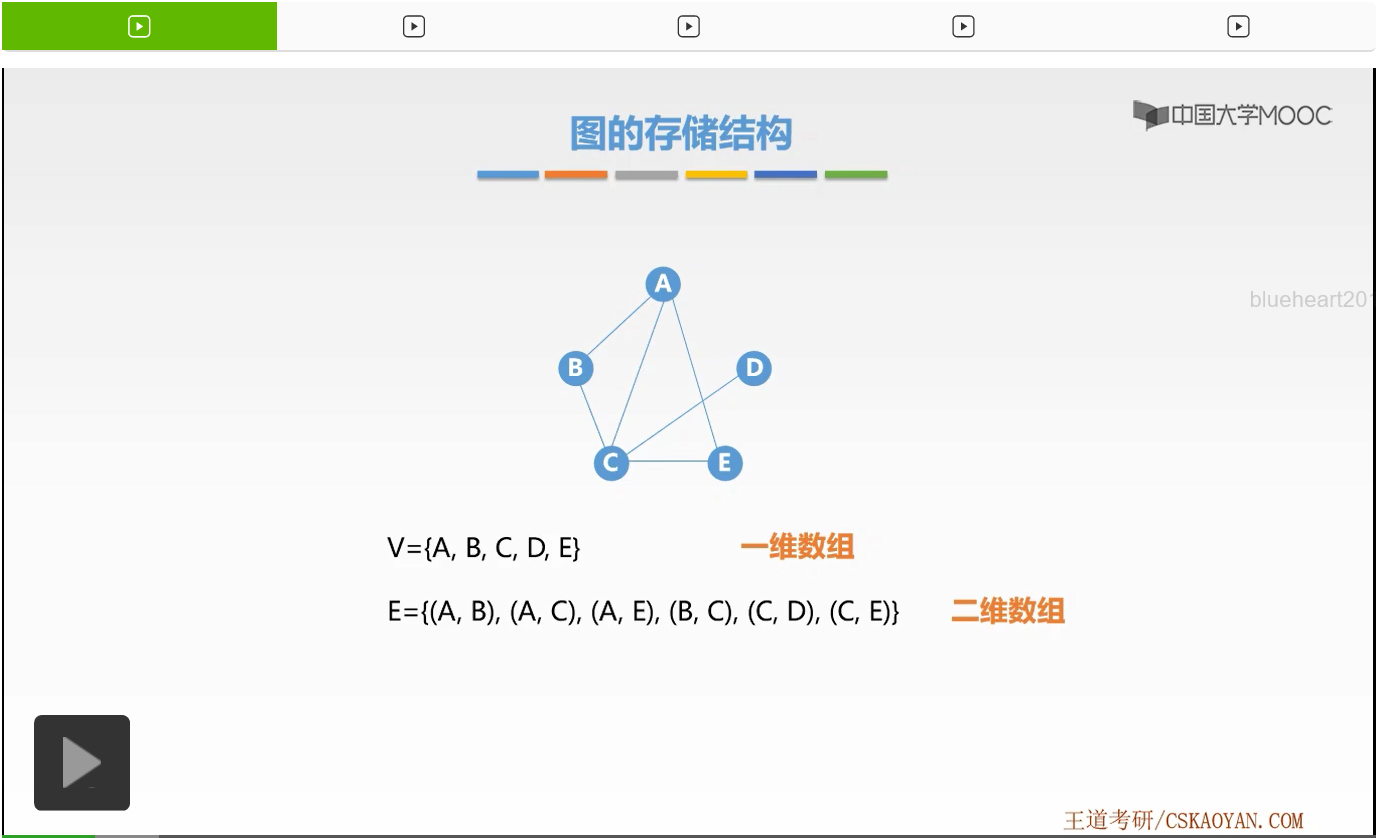
我们称这样二维数组表示的矩阵为邻接矩阵。
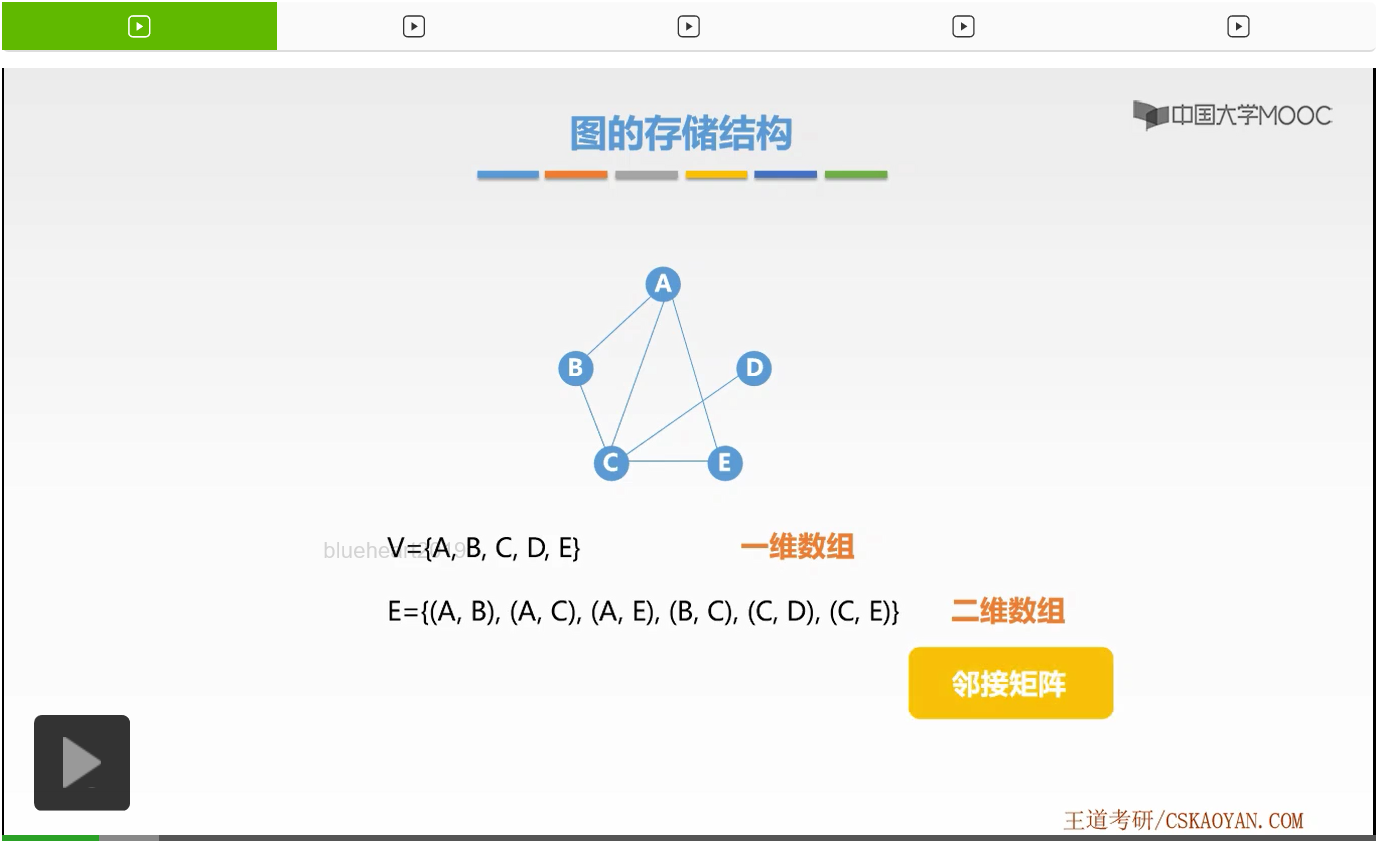
好,接下来我们来学习邻接矩阵法具体是如何对图进行存放的。首先,我们规定
本节课我们来学习图的第二种存储方式,就是邻接表法。
上一节课我们学习了图的邻接矩阵法。对于这样的图我们可以用一个邻接矩阵,用一个矩阵来存储它所有的结点的关系,也就是边的集合。那么我们发现在这样的矩阵当中,如果边的数量非常少的话,它会造成很多空间的浪费,也就是很多空间并没有实际的存储意义。
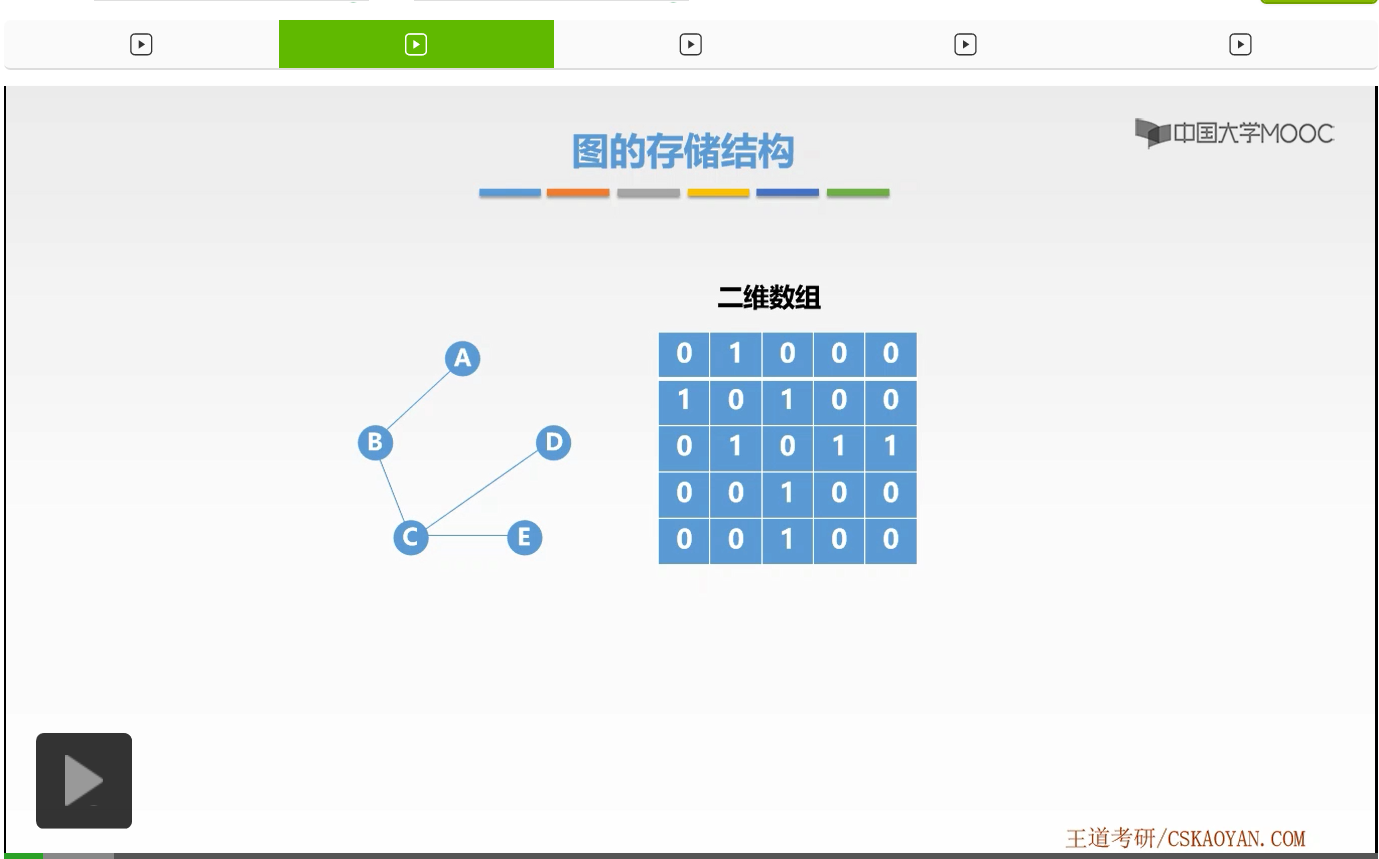
那么对于这样边稀少的图也就是我们所说的稀疏图,其实采用邻接矩阵法它的存储效率会非常低,会有许多空间造成浪费。
所以本节课我们来讲解图的第二种存储方式,就是邻接表法。我们知道邻接矩阵法是采用了一个矩阵存放各个顶点之间的关系,也就是我们所说图的边的集合。那么邻接表法是如何来存储这些边的呢?其实它是为每一个顶点建立了一个单链表来存放与它相连的边,这样来存放边的集合。在邻接表法中,主要有两种表。第一种与邻接矩阵法类似,它有一个存放顶点的顶点表。但是它与邻接矩阵法还有一点不同,我们来看有什么样的不同。它依旧是采用顺序存储,也就是采用数组来存放各个顶点。但是每个数组元素存放的不仅仅是顶点的数据部分,还有一个是边表的头指针,也就是刚刚我们所说的为每一个顶点建立的单链表。那么存放它的头指针来指向这一个单链表。那么第二种表就是我们所说的这些单链表它们叫做边表,在有向图当中也叫做出边表。这些边表采用的是链式存储,就是单链表,单链表中存放与一个顶点相邻的所有的边。每一个单链表的结点表示的是一条从该顶点到链表结点顶点的边。大家注意一下,这里是其实是有方向的。它是从该顶点出发,到我们所说的下一个端点的这样一条边,它是一条有方向的边。所以在有向图当中我们也称作为出边表,我们是从这个顶点出发的边。好,这就是两种表,一种是顶点表,一种是边表。
我们发现在邻接表法当中采用的是顺序存储加上链式存储这样的存储方式。好,我们来看一下顶点表和边表的结点结构。首先来看顶点表的结点结构。
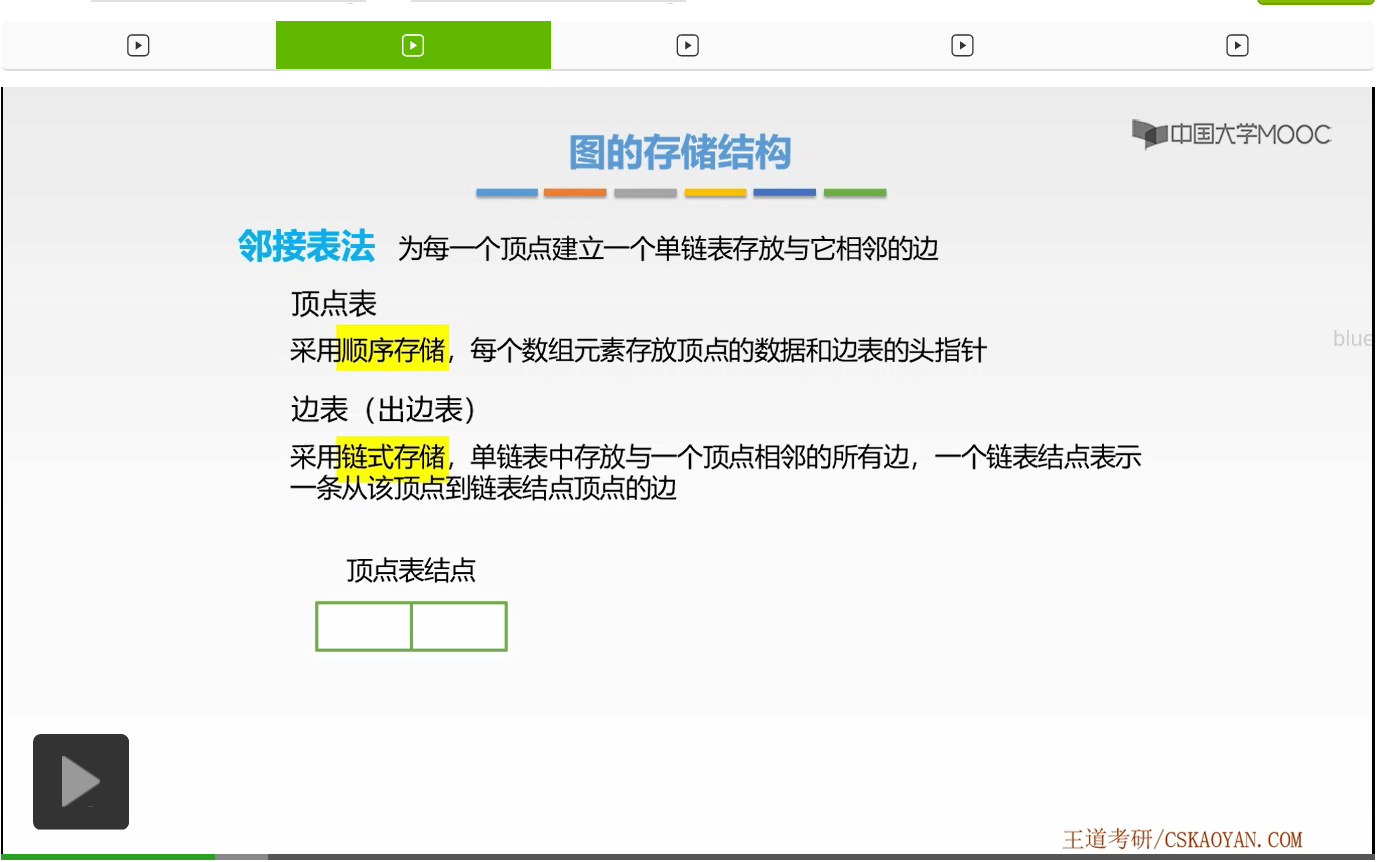
顶点表结点结构一直有这样两块域,第一个域是存放数据的data域,第二个域的部分是存放它的单链表的头指针的部分,这是一个指针域。好,这是顶点表结点。接下来我们来看边表结点。边表结点依旧有两块域,它与我们单链表的结点结构其实是相似的,依旧有存放数据的部分和存放下一个结点的指针部分。当然这里的数据存放的其实是该条边的另一个端点,在有向图当中也就是,弧头位置的这个端点。而指针域则是存放下一个边表结点的地址也就是指针。好,这就是顶点表结点的结构和边表结点结构。
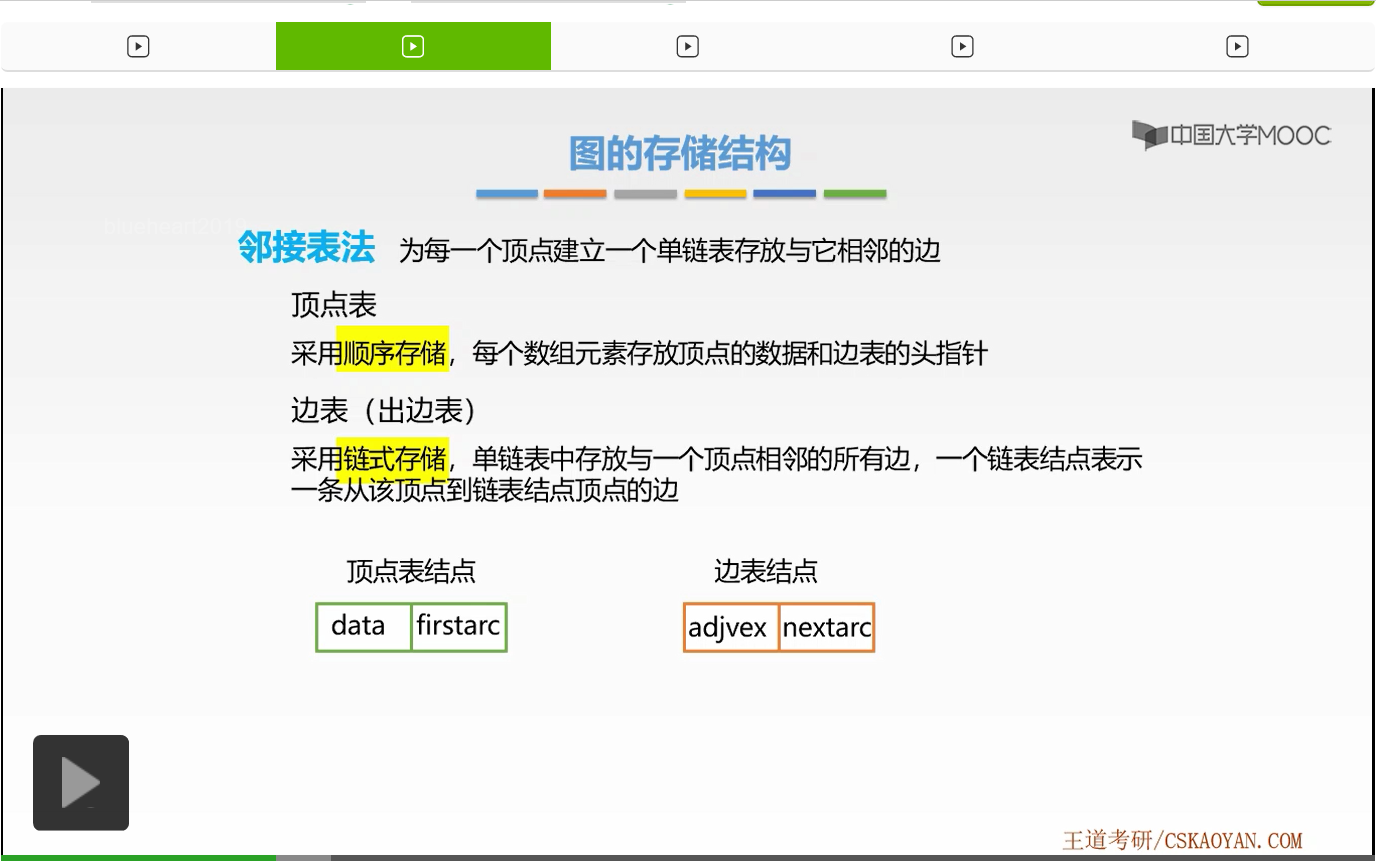
好,这就是邻接表法。接下来我们来看一个邻接表法的例子,来看一下它如何实现存储的。这是一个有向图。首先我们要建立关于它的顶点表。它一共有5个顶点,所以在顶点表的数组当中我们要建立5个数组元素。那么这5个数组元素每一个数组元素依旧有两个域,第一个域是存放顶点数据的数据域,在这里就是我们所说的A、B、C、D、E。那么第二个域则是指向边表的头指针,那么接下来我们就来建立每一个顶点的它的边表。那么首先我们来看顶点A,顶点A没有任何边是从它出发的,没有任何边的弧尾部分是在顶点A,所以它的边表其实为空,它的单链表为空。那么接下来我们再来看顶点B,顶点B有两条边是从顶点B出发的,那么它的弧尾位置都在顶点B。所以它的边表结点有两个结点,第一个结点是从B指向A的这一条边,第二条边是从B指向C的这条边。我们发现在边表结点的中间的数据部分,我们存放了一个0和2。该0表示的是对应结点的数组下标,我们通过0就可以找到下一个端点的位置。所以0对应的就是我们所说的顶点A,而2对应的就是我们数组下标下的顶点C。好这样我们就建立了它的边表。接下来我们来看顶点C。顶点C依旧有两个边表结点,依旧是一个指向D的这样一条边。那么D的下标是3,所以这里边表结点存放的数据是3。接着依旧建立下一个边表结点。这里这条边的弧头部分是E,所以它的数据部分为4,表示E的数组下标。好,接下来我们来看顶点D。顶点D依旧没有任何边是从它出发的,没有任何边的弧尾位置在顶点D,所以它的边表也就为空,而E也依旧为空。这样我们就用了邻接表法建立了一个有向图的边表。好,在邻接表法当中我们发现,如果我们需要有边的存在我们才建立结点,而如果没有边的存在那么我们则不需要建立结点。所以它会节省空间。
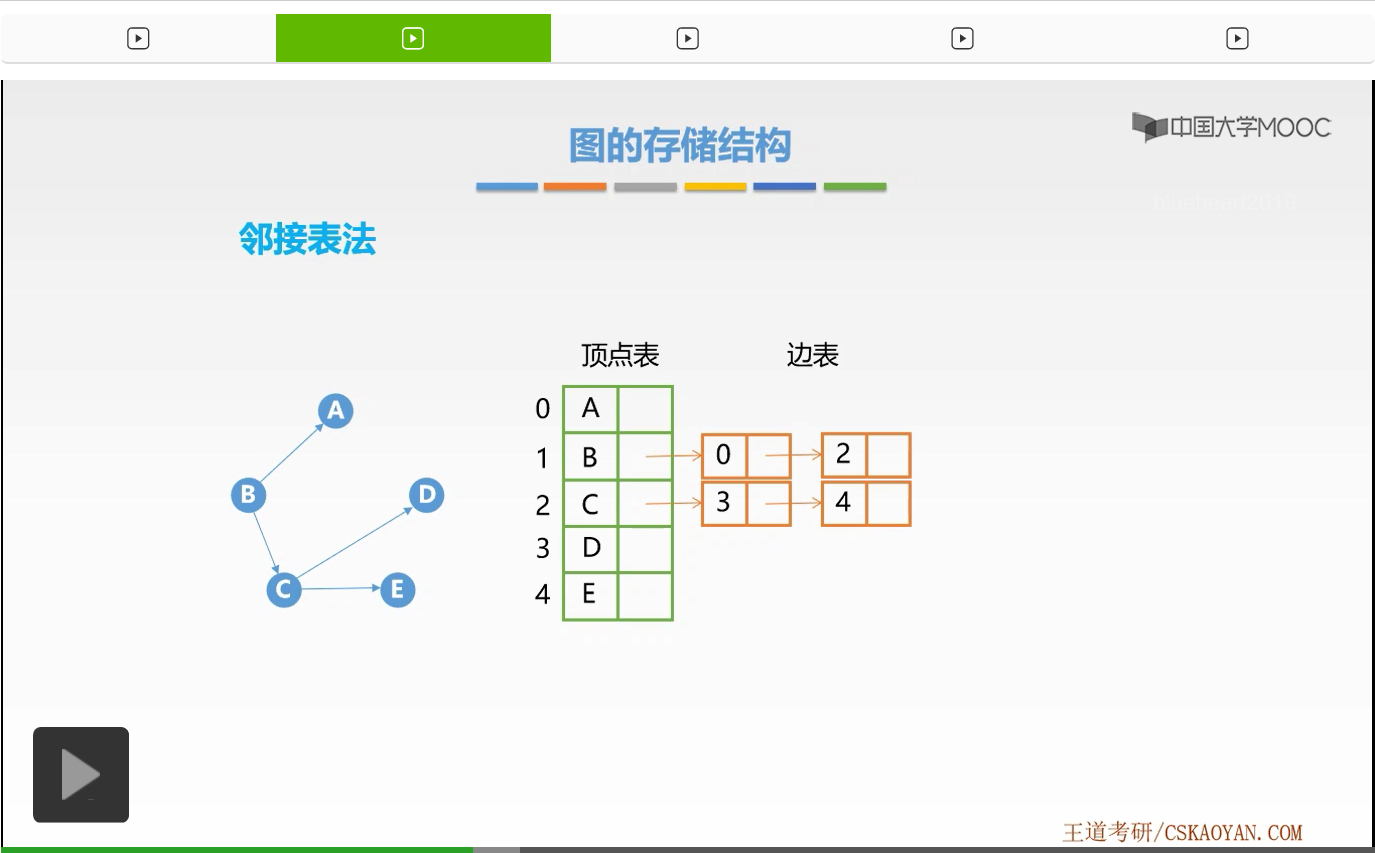
好,接下来我们来看一个无向图的例子。这是一个无向图,每一条边我们都换成了无向边。那么它与有向图有什么样的区别呢?我们来看它是如何建立的。首先,它还是要建立属于它的顶点表,依旧有5个数组元素因为有5个结点,数据域也就存放了A、B、C、D、E这样的数据部分。接下来我们就来建立它的边表。首先我们来看顶点A,顶点A它是不是与有向图是不一样的?因为有向图它边是有方向的,而在无向图当中其实它是没有方向的。所以对于顶点A来讲是不是有与它相连的边啊。那么这一条边它另一个端点是B,所以这里数据域部分存放了B。那么我们再来看B,B
各位同学大家好,本节课我们就来学习图的第三种存储结构叫做十字链表。
什么是十字链表呢?首先我们应该知道,十字链表一定是针对有向图的一种链式存储结构。首先,十字链表是存储有向图的。
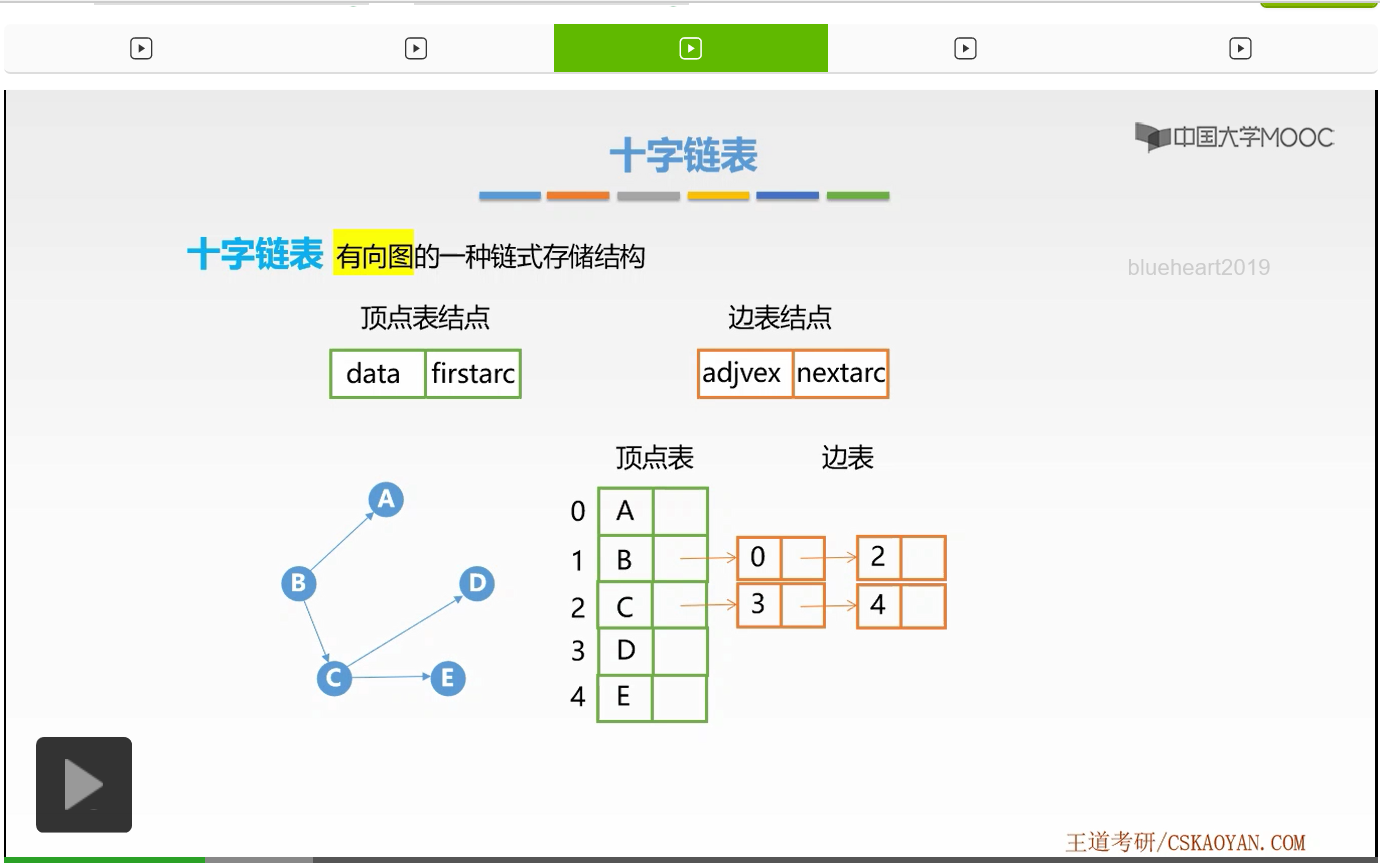
另外,它是一种链式存储结构。那么,我们之前也学习过一种链式存储结构叫做邻接表。我们先来简单回忆一下什么是邻接表法。那么在邻接表法当中我们有两种表,大家还记得吗?第一种表是顶点表,每个顶点表由若干个顶点表结点构成,它们存放在数组当中。那么每个顶点表结点他们有两块域,第一个域是存放该顶点数据的data域,第二个域是存放指向属于它边表的头指针。那么接下来还有另外一种表叫做边表。在边表当中有边表结点,那么边表结点依旧有两块域,第一个域存放的是该弧指向弧头部分的顶点,第二个域是指向下一个边表结点的指针。好,这就是邻接表法的两个表。

接下来我们来看一个有向图的例子。这是一个有向图,我们用邻接表法来存放它。这是它的邻接表,那么根据我们之前的学习我们知道,在邻接表法当中,寻找某一个顶点所有的出边,也就是以该顶点为弧尾的弧是非常容易的。但是找到某一个顶点所有的入边,是非常困难的,我们要遍历整个边表,也就是所有顶点的边表才能找到该顶点所有的入边。
所以根据这样的弊端,我们引出了十字链表这样一种新的存储结构。在十字链表当中,我们寻找某一个顶点的出边很简单,我们寻找某个顶点的入边也非常简单。那么接下来我们就来学习十字链表,我们来看一看十字链表是如何达到这样的特点的。那么十字链表它改变了我们对应的顶点结构以及边表结点的结构。我们来看看,与之前有什么样的不同。好,那么根据这样的要求,在十字链表当中我们不仅仅要像邻接表当中我们要存放一个顶点的出边,它的所有出边也就是对应的出边单链表,我们也要保存一个顶点所有的入边,也就是也要保存它的入边单链表。所以根据这样的要求我们就要修改对应的结点结构。
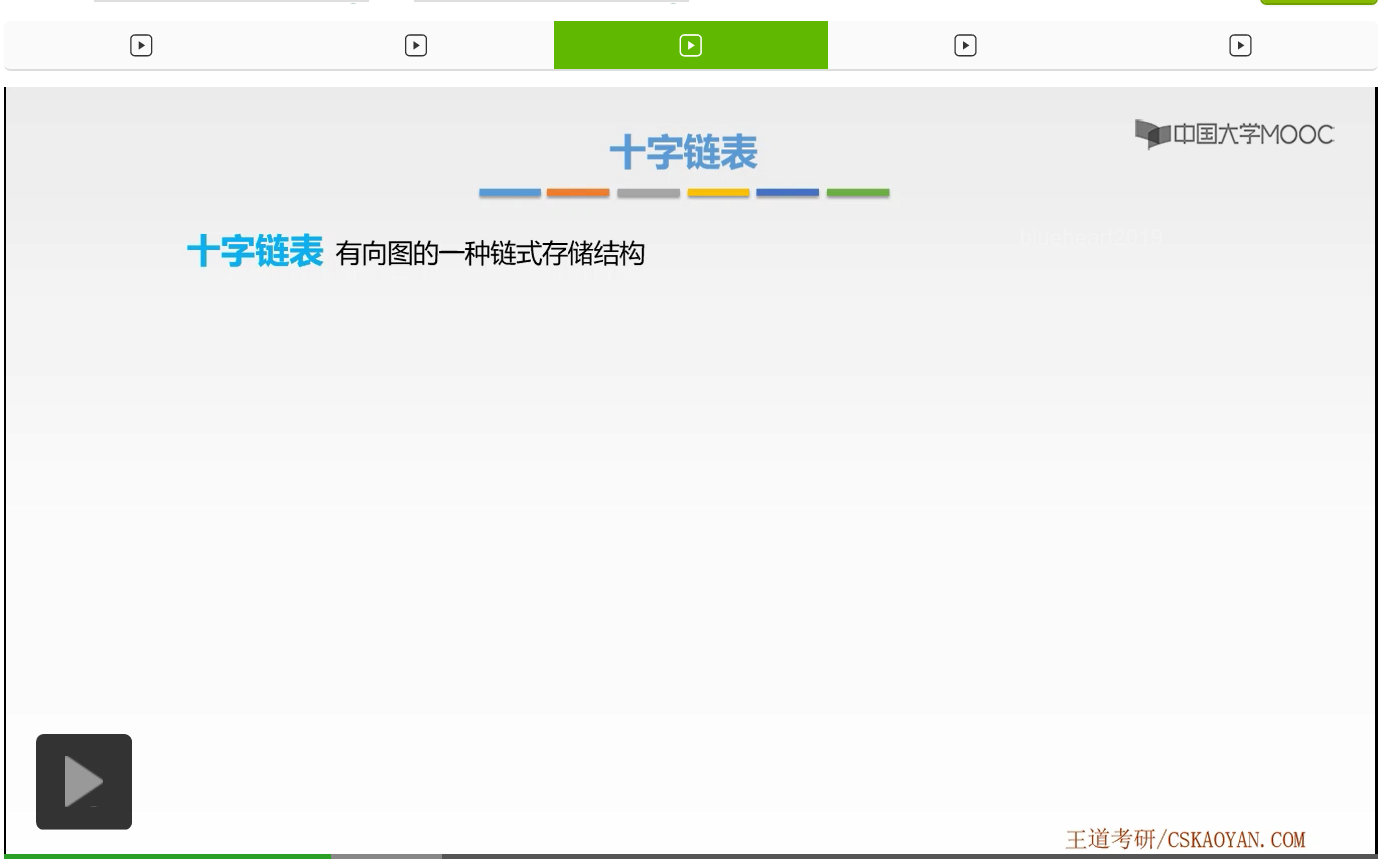
我们来看我们是如何进行修改的。其中顶点表结点我们分为了三个域。第一个域依旧是存放数据的数据域,而之后两个域存放的则是出边单链表和入边单链表的头指针。那么第一个firstin存放的则是入边单链表的第一个结点的指针,而第二个firstout存放的则是出边单链表的头指针,也就是它第一个结点的指针。好,这就是顶点表结点的结点结构。好,接下来我们来看一下我们对边表结点做出了哪些修改。我们将它重新划分为5个域,这5个域表示的是什么呢?我们一起来看。第一个域是伪域,它存放的是该弧弧尾的端点。那么第二个域则是头域,它存放的是该弧弧头部分的端点。接下来的两个域hlink和tlink它是指针域,第一个hlink它存放的是弧头相同的下一条边,也就是下一个边表结点的指针。那么第二个域tlink存放的是下一个弧尾相同的结点的指针。那么这是hlink和tlink,它们是两个指针域。接下来的最后一个域,是存放该边的数据。如果该边是有权重的话,我们则要存放一个info数据来表示它的权值。而有的时候我们也会发现我们只有4个域,因为我们将最后一个权值的这个info域给忽略掉了。好,这就是我们修改过后的顶点表结点和边表结点的结点结构。好,接下来我们就来看一个小例子,看一下是如何将这些结点组合成一个十字链表的。
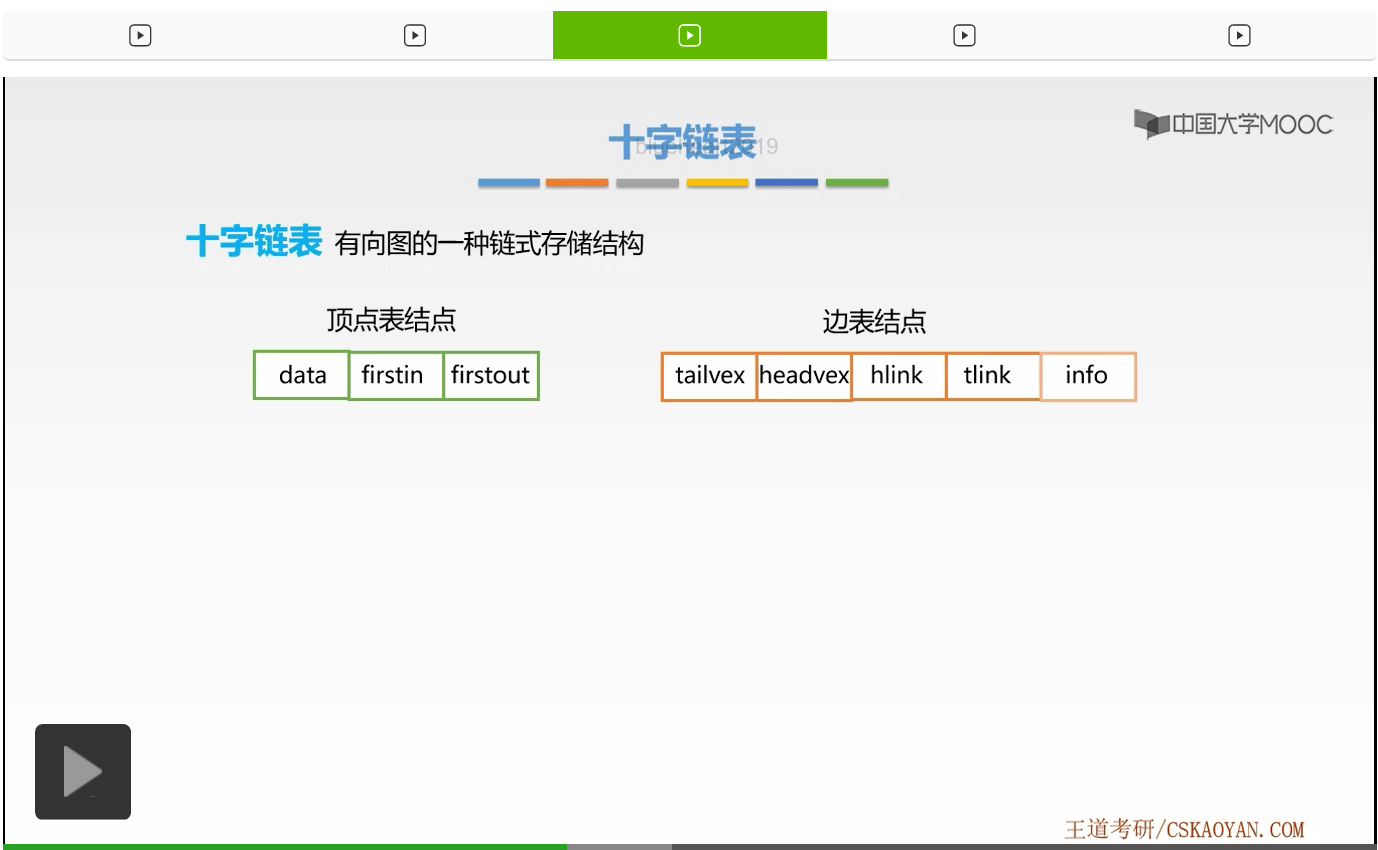
首先这是一个有向图。我们接下来还是要形成它的顶点表,因为该有向图有4个顶点,所以顶点表有4个顶点表结点依旧存放在数组当中,所以它对应的前面0、1、2、3是数组下标,接着我们要将数据部分进行依次地赋值,A、B、C、D。好,接下来我们就来形成它的边表了。怎样形成边表呢我们来看,第一条边那么就是顶点A这样一条出边,从A到D的这样一条弧。那么首先该边是顶点A的出边,所以我们要修改顶点A的firstout的指针,也就是它的出边单链表的头指针,将它指向该结点。那么接下来我们来修改该边表结点的对应的域。
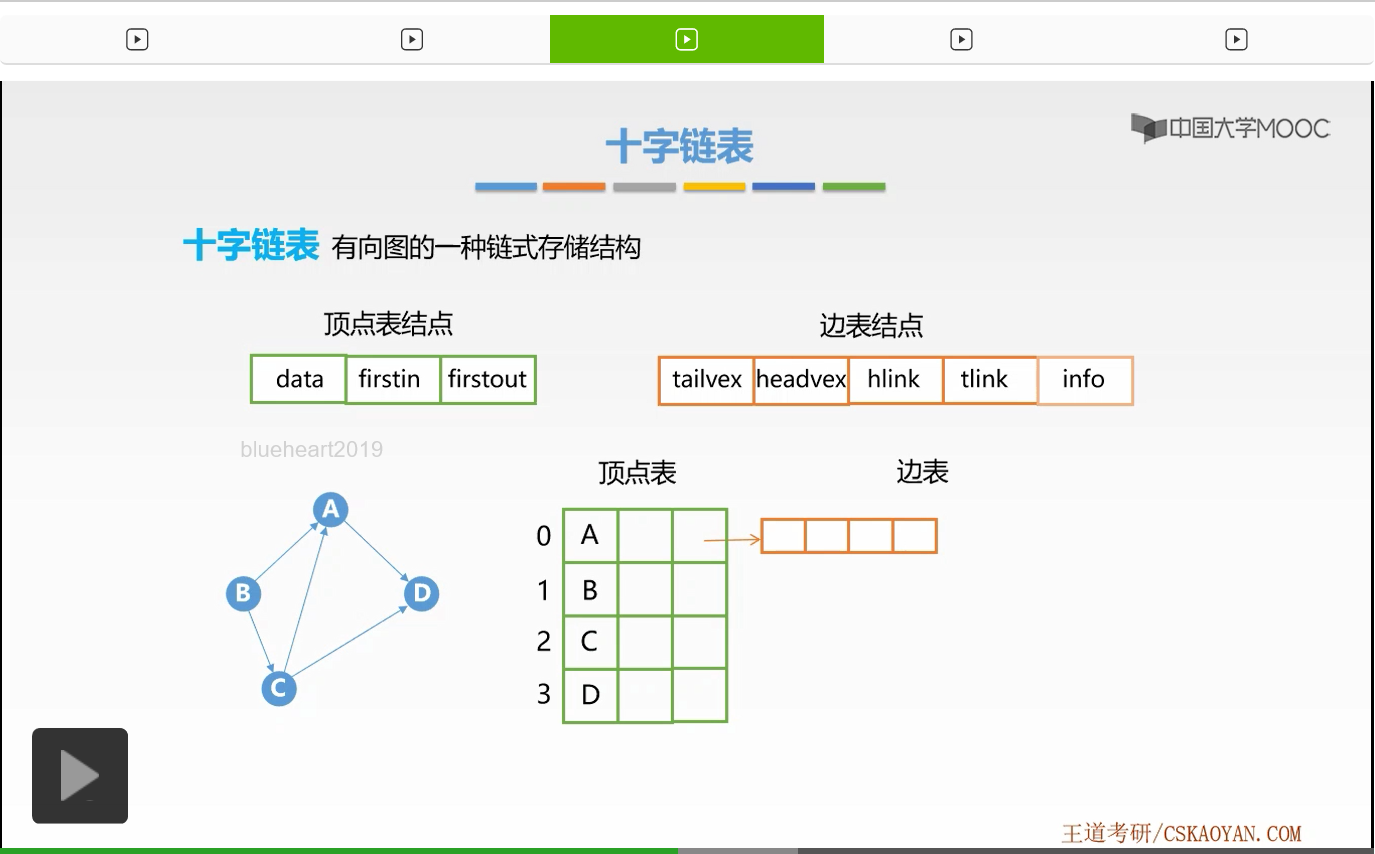
那么因为它的弧尾部分是顶点A,弧头部分是顶点D,所以将两个域修改为对应A和D的数组下标也就是0和3。好,这样我们就形成了第一个边表结点吗?我们是不是还忘记修改了一个指针啊,也就是顶点D的firstin指针,它的入边单链表的头指针。
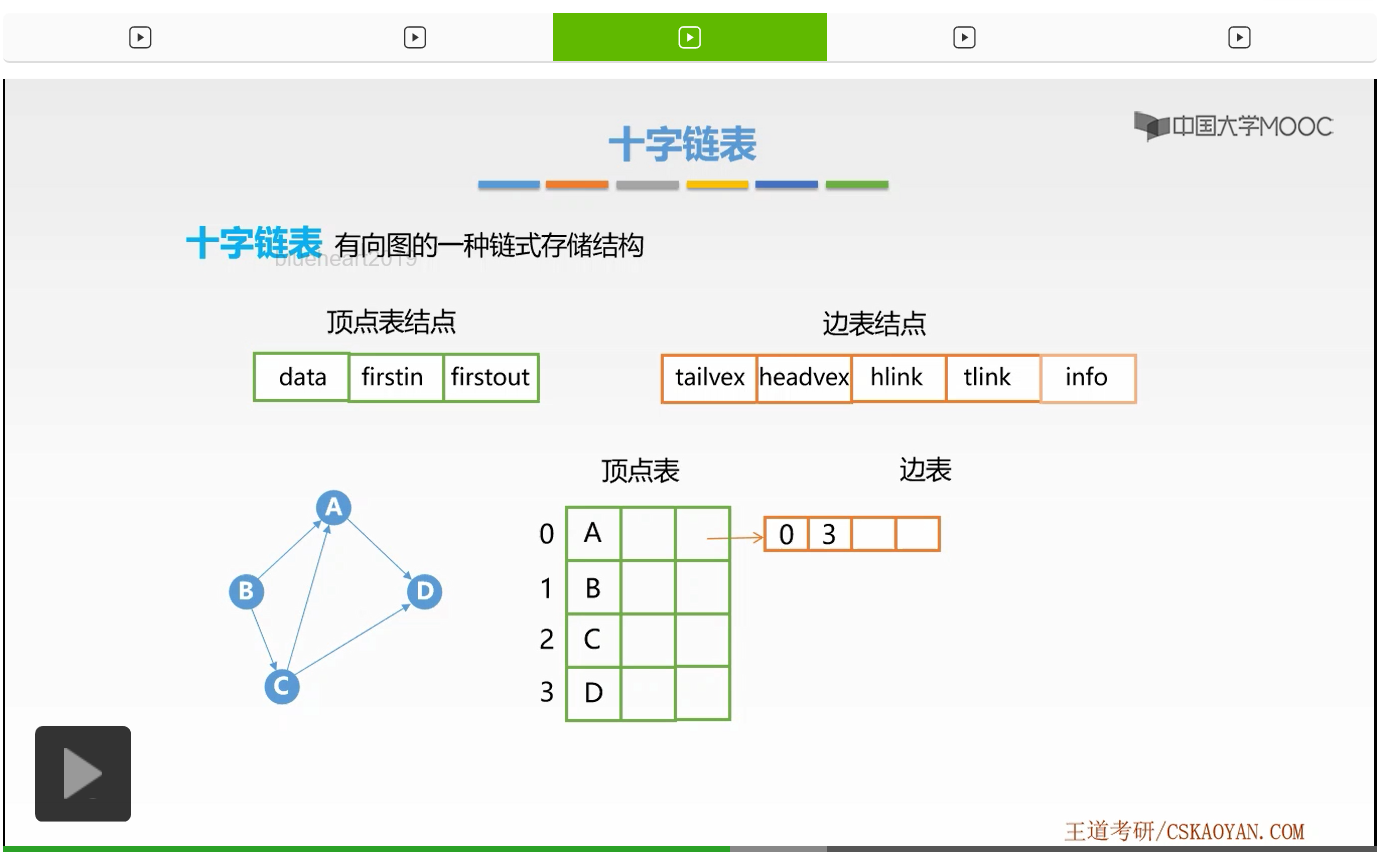
我们要将它指向该边表结点,因为该弧是顶点D的一条入弧。好,接下来我们来欣赏下一条边。那么我们来看顶点B,顶点B有两条出边,第一条是从B指向A的这样一条边。
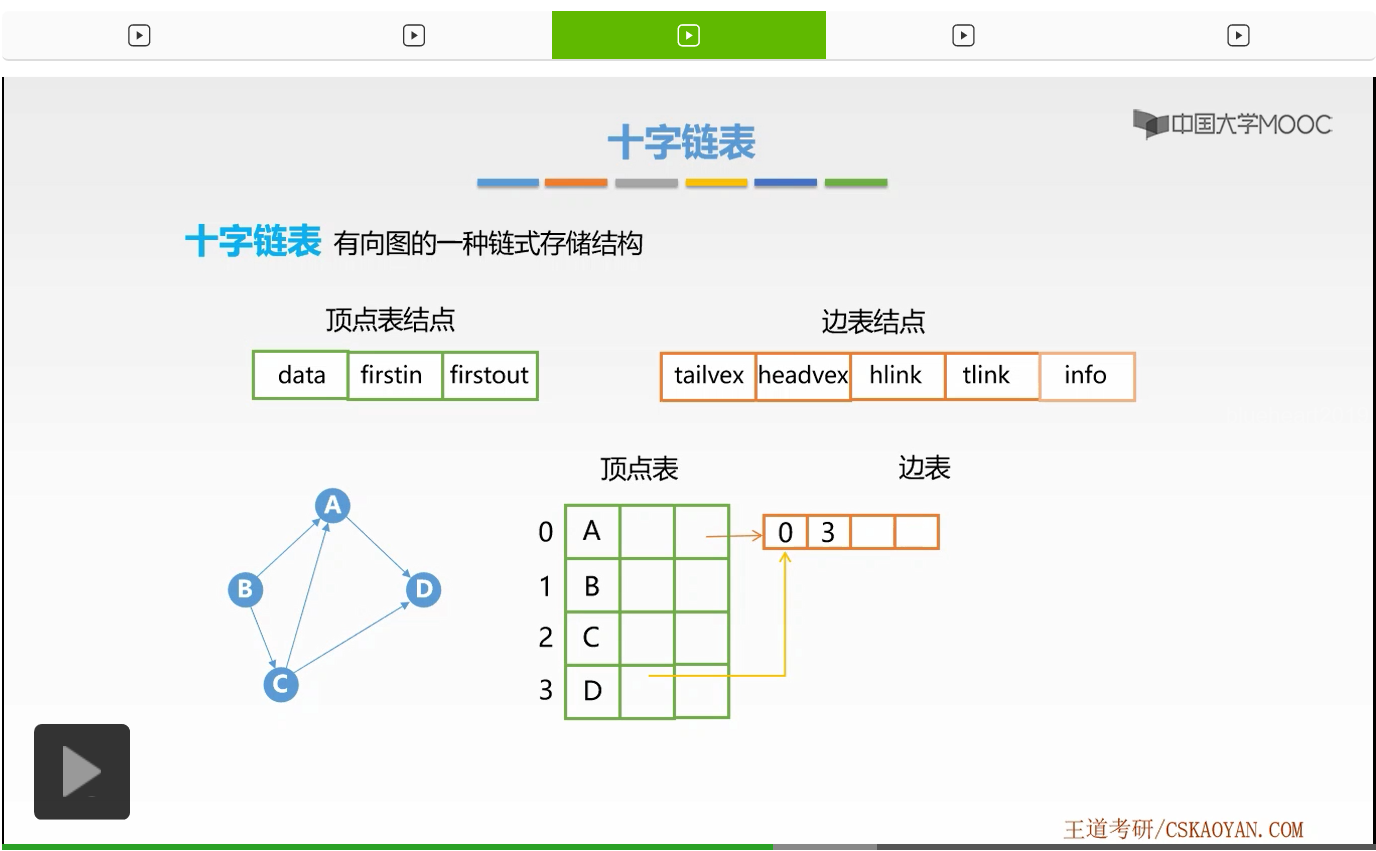
那么依旧我们要将顶点B的firstout指针指向该结点,并对该结点进行赋值。那么,它的尾域要修改为1,头域要修改为0,对应的是B和A的数组下标。接下来我们来修改什么呢?是不是依旧是顶点A的firstin啊,一直将顶点A的入边单链表的头指针指向该结点。好,这样我们就形成了下一个边的边表结点。
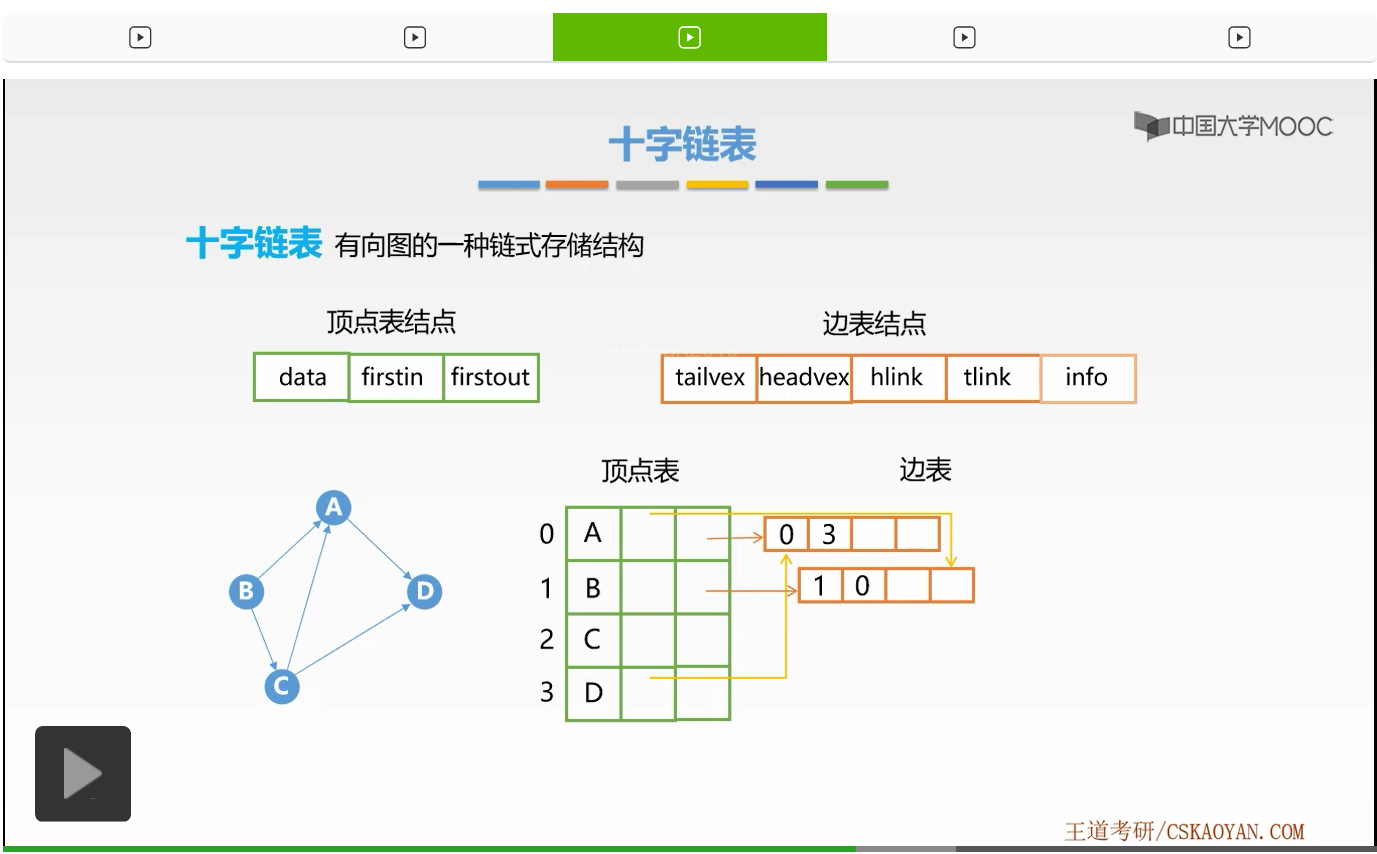
那么接下来我们来看下一条弧BC,那么这儿依旧是B的一条出弧,所以我们要将上一个B的出弧的这个边表结点的tlink域指向该结点,然后对该结点进行赋值。那么它的弧尾部分是B,弧头部分是C,所以对应的数组下标是1和2。接着它的弧头部分的端点是不是2啊,所以要修改C的firstin指针,将它指向该结点。好,这样我们就形成了B->C这样一条有向边。接下来我们来看C端点,C端点有两条有向边,从C指向A的这样一条有向边,也就要形成了对应的链表结点。

依旧因为它是C的出边,所以要将C的firstout指针指向该结点,那么对应我们修改它的尾域和它的头域。

接下来我们发现它是不是与B、A也就是1、0的这个边表结点它的头域是相同的呀,所以我们要将1、0这个边表结点的hlink指向该结点,将它串起来。
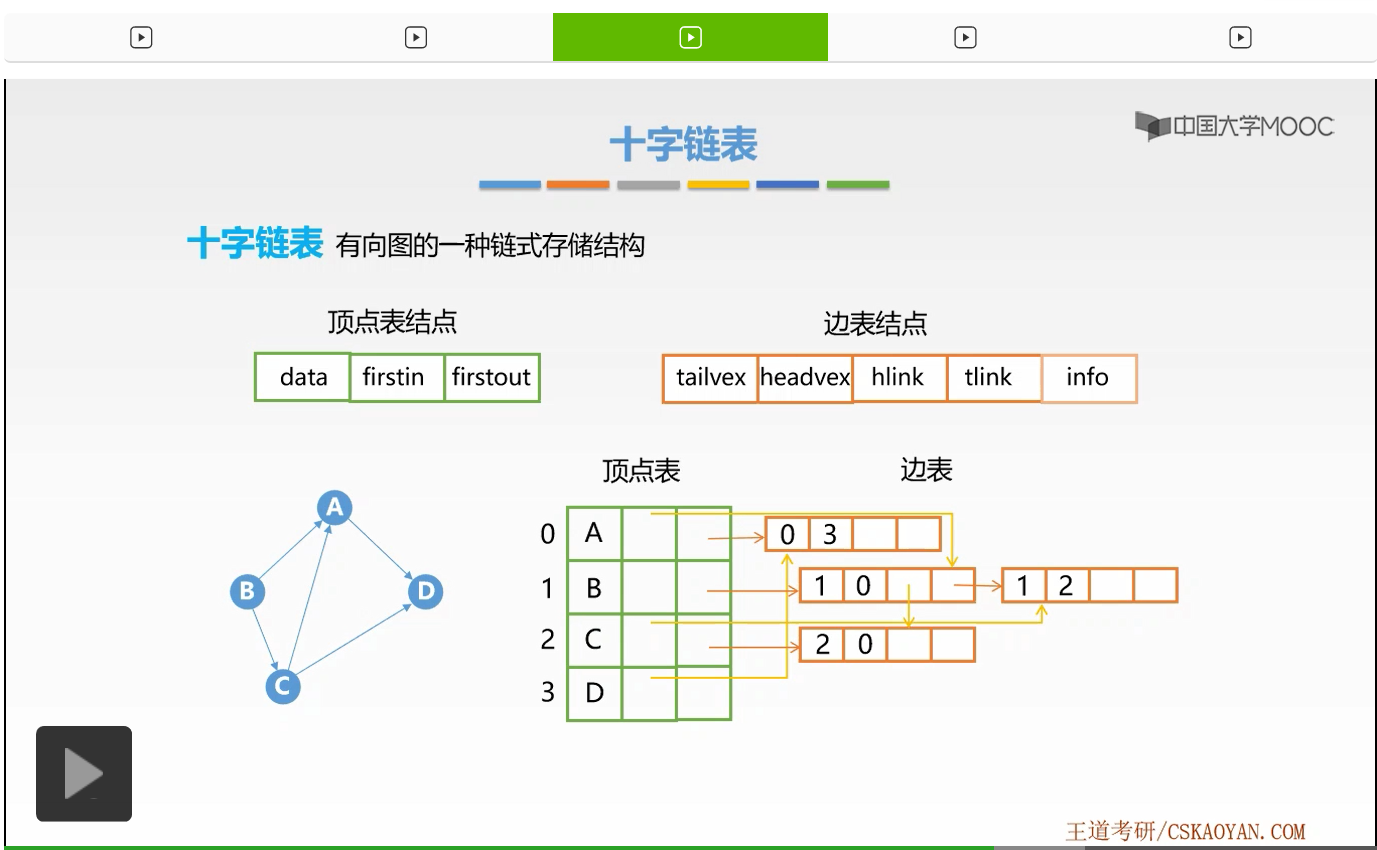
那么接下来我们还剩下C、D这样一条边,那么它依旧是顶点C的出边,所以要将它连接到它的出边单链表上,接着依旧修改它的尾域和头域。那么它的头域与哪一个边表结点相同呢?它是不是与03这一个边表结点相同啊。说明它们的弧头指向了相同的顶点也就是顶点A,所以要将它们串起来。也就是将03这个结点的hlink指向23这个结点。这样我们就形成了C->D这条边的边表结点。好,5条边我们已经都生成了它的边表结点,这样我们就生成了对应该有向图的十字链表。那么我们在该十字链表当中找到某一个顶点的出边我们可以根据它的出边单链表依次地遍历,那么我们如果想要找到某一个顶点的入边,则我们要从它的入边单链表的头指针开始依次地遍历它的入边单链表就可以了。好,这就是十字链表。
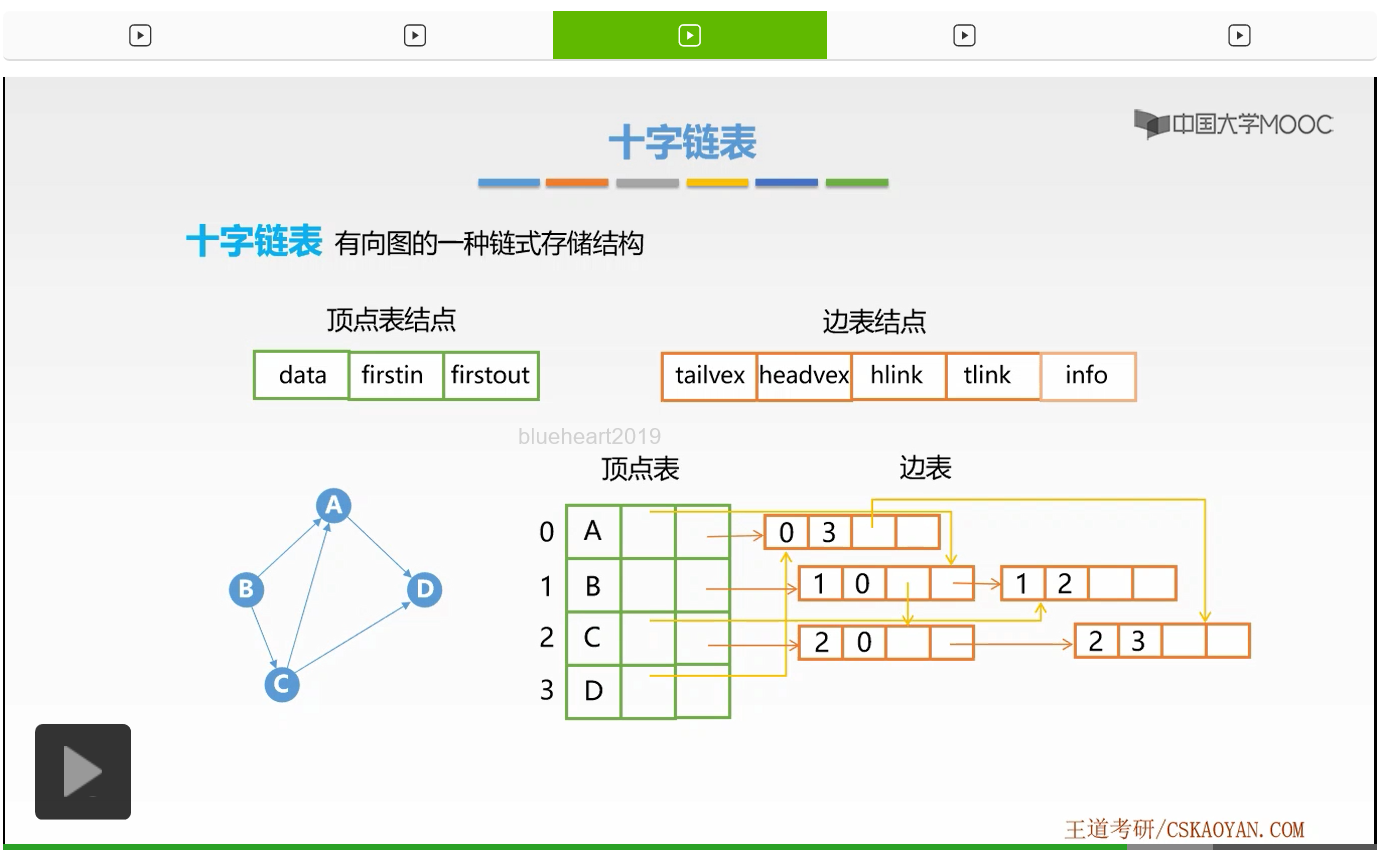
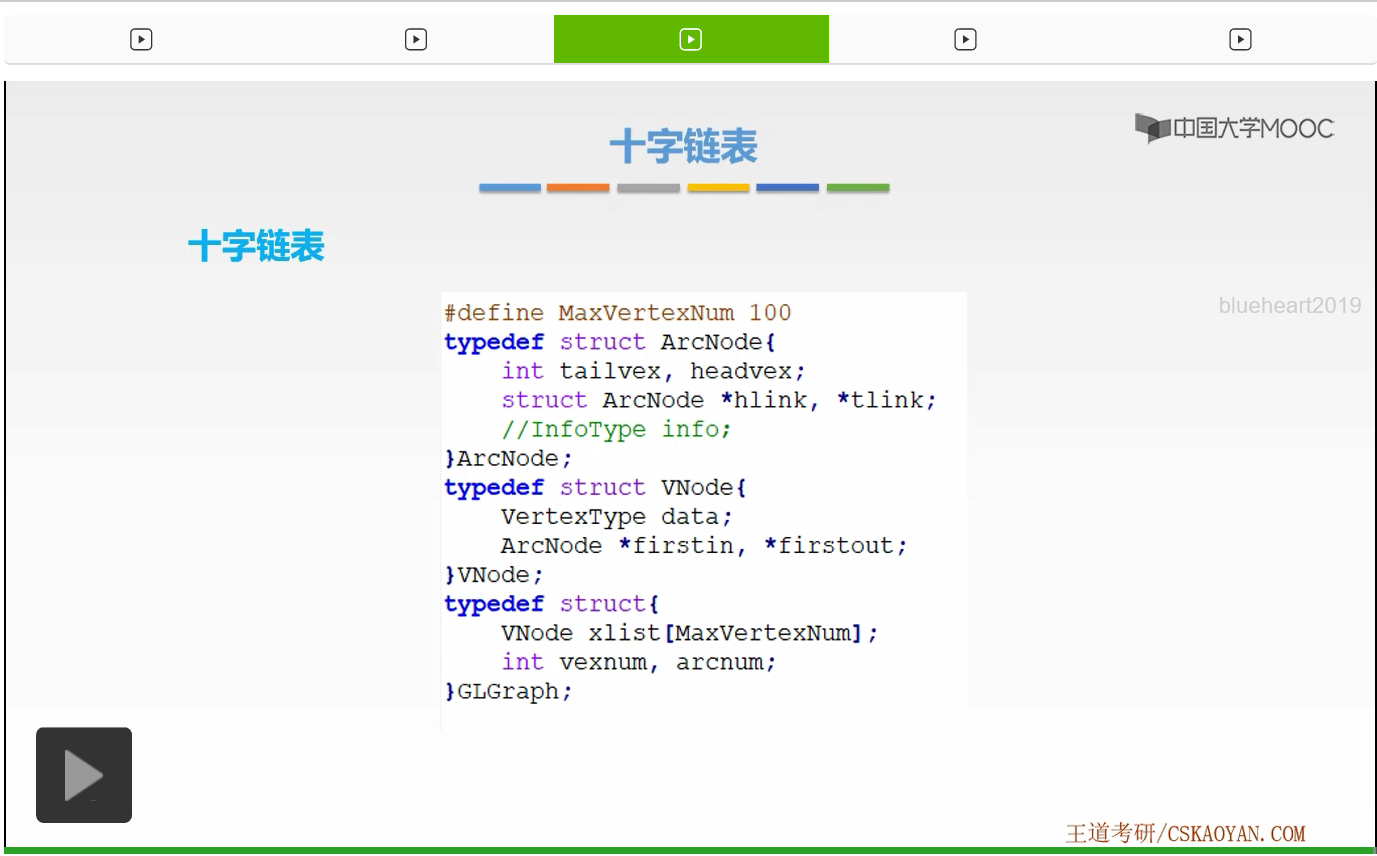
那么最后我们还是来看一下十字链表它是如何用语言来定义的。它与邻接表相同,也就有这样三个结构体,分别表示是它的边表结点以及它的顶点表结点,最后是十字链表。首先我们来看它的边表结点。边表结点这里有4个变量,首先我们要表示它的尾域和头域,这里我们用两个整型变量来表示了尾域和头域。因为我们知道我们对应的顶点是用数组下标来表示,所以这里用整型变量就可以表示对应的顶点了。接下来是两个指针,分别是hlink和tlink,维护的是出弧单链表和入弧单链表。那么最后这一个注释掉的变量,依旧是表示的是对应弧的权重。如果它有的话,我们要增加这一个保存权重的这一个变量info。好,这就是对应着边表结点的结构体定义。那么接下来我们来看一下顶点表结点的结构体定义。那么它有三个变量,第1个变量是保存数据的data,接下来的后两个变量是保存入弧单链表头指针的firstin以及出弧单链表头指针的firstout。最后就是这个十字链表了。那么因为我们所有顶点是存放在数组当中的,所以这里我们生成了一个数组。xlist保存了所有顶点表结点以及顶点表结点对应的结构体。那么之后依旧有两个整型变量,表示的是顶点的数量以及边的数量。好,这就是十字链表的语言定义,它与邻接表相同,其实对于某一个有向图的十字链表并不一定唯一。但是每一个十字链表都可以表示成一个唯一的有向图。
学习图的最后一种存储结构叫做邻接多重表。上节课我们学习了十字链表,我们知道十字链表是针对于有向图的一种链式存储结构,
那么本节课所要学习的邻接多重表其实是针对于无向图的一种存储结构。

它是对无向图进行链式存储的一种方法。那么提到链式存储结构,我们一定还会想到之前我们所学习过的邻接表,邻接表有两种表,顶点表以及边表。顶点表结点和边表结点。
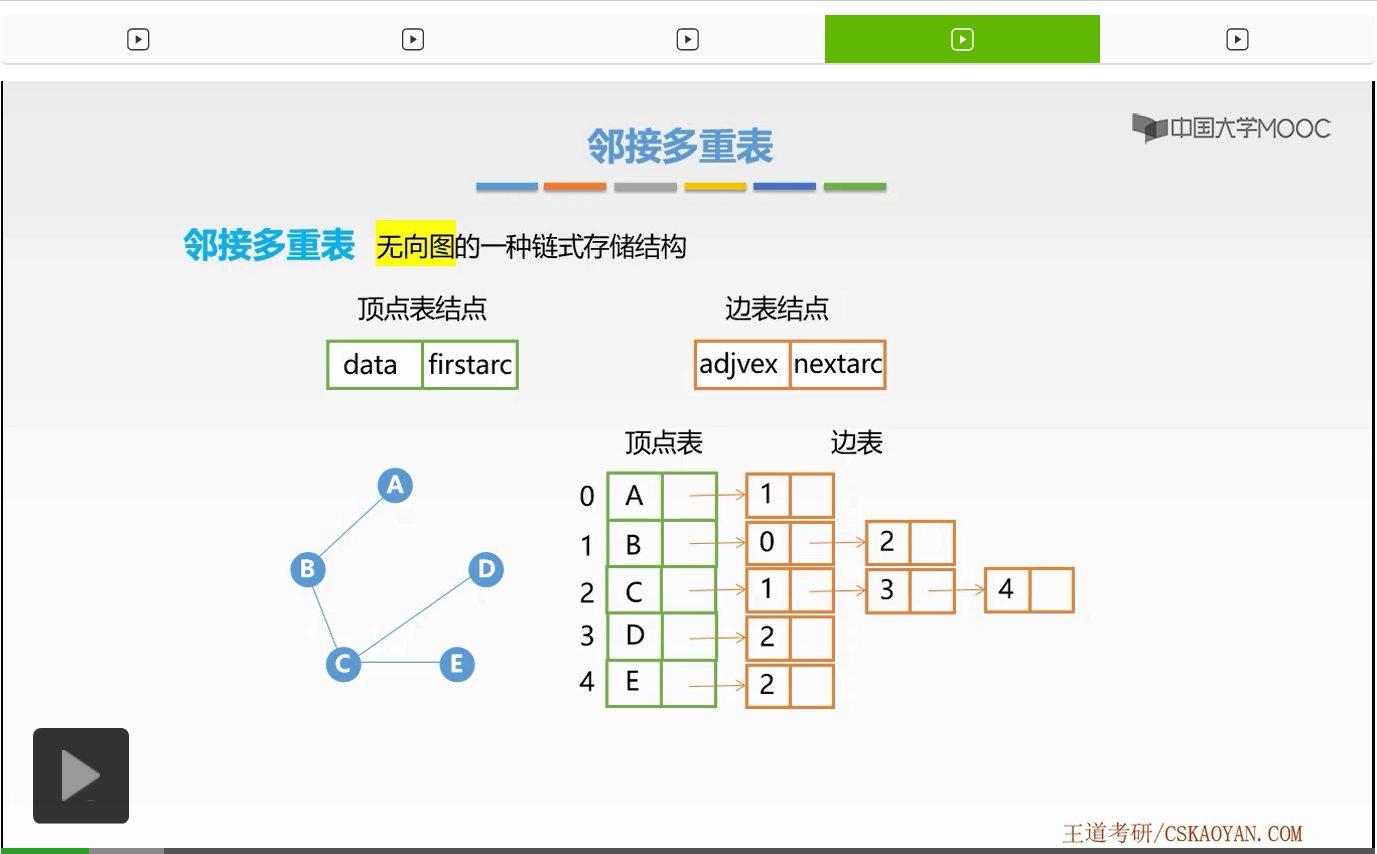
那么对于这样的无向图我们可以采用邻接表对它进行存储。我们知道在邻接表存储无向图时,每一条无向边我们要用两条有向边也就是两个边表结点来代表一条无向边。
那么我们对于某一条无向边的删除操作时,在邻接表法当中我们只要删除两个边表结点,我们要遍历两个顶点的边表来找到对应的边表结点并把它进行删除。那么其实这样操作效率是比较低的。
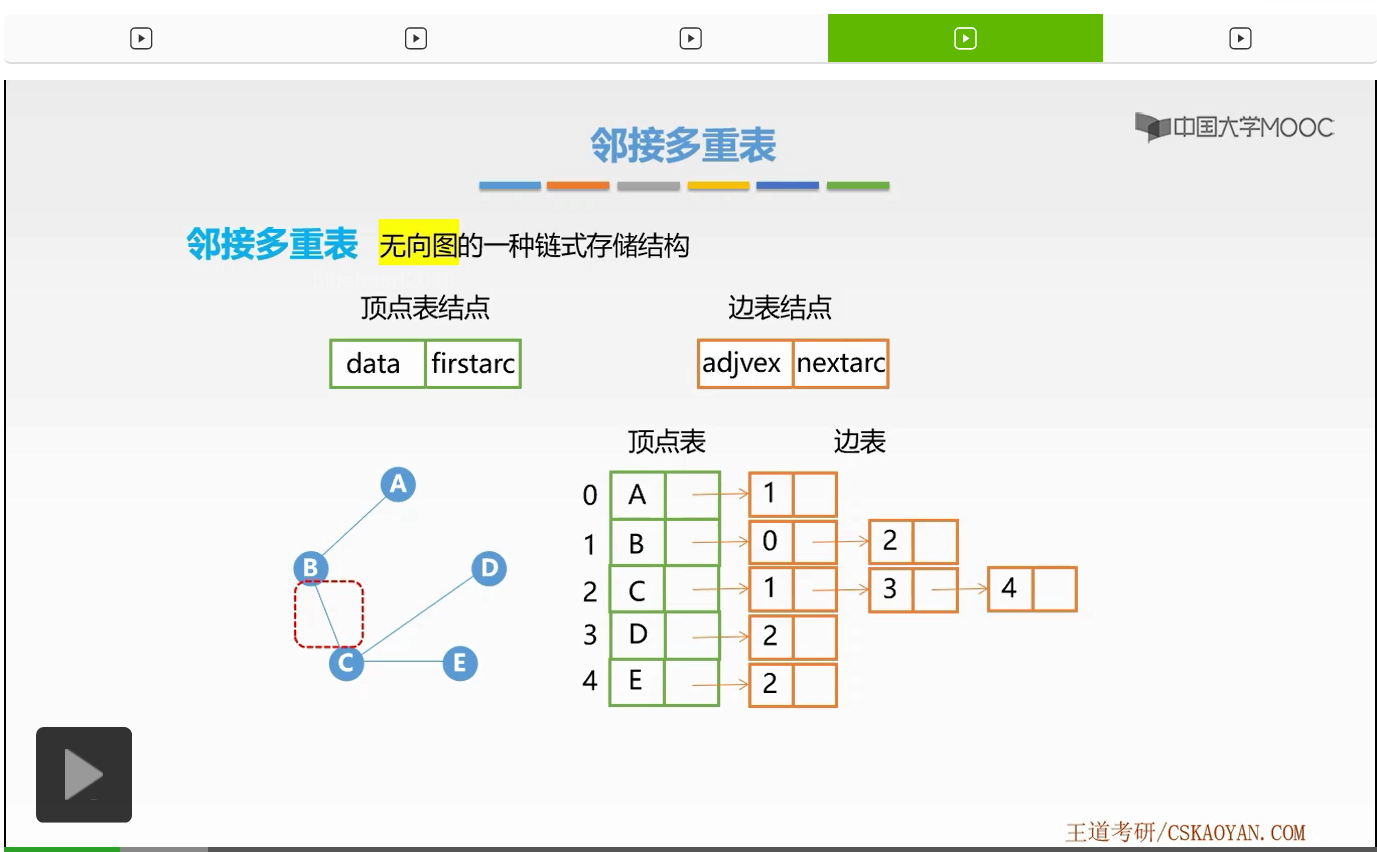
所以我们就引入了今天所要学习的这个临接多重表。那么接下来我们就来看,邻接多重表是如何优化了我们之前所学习过的邻接表来达到这样删除效率提高的目的。
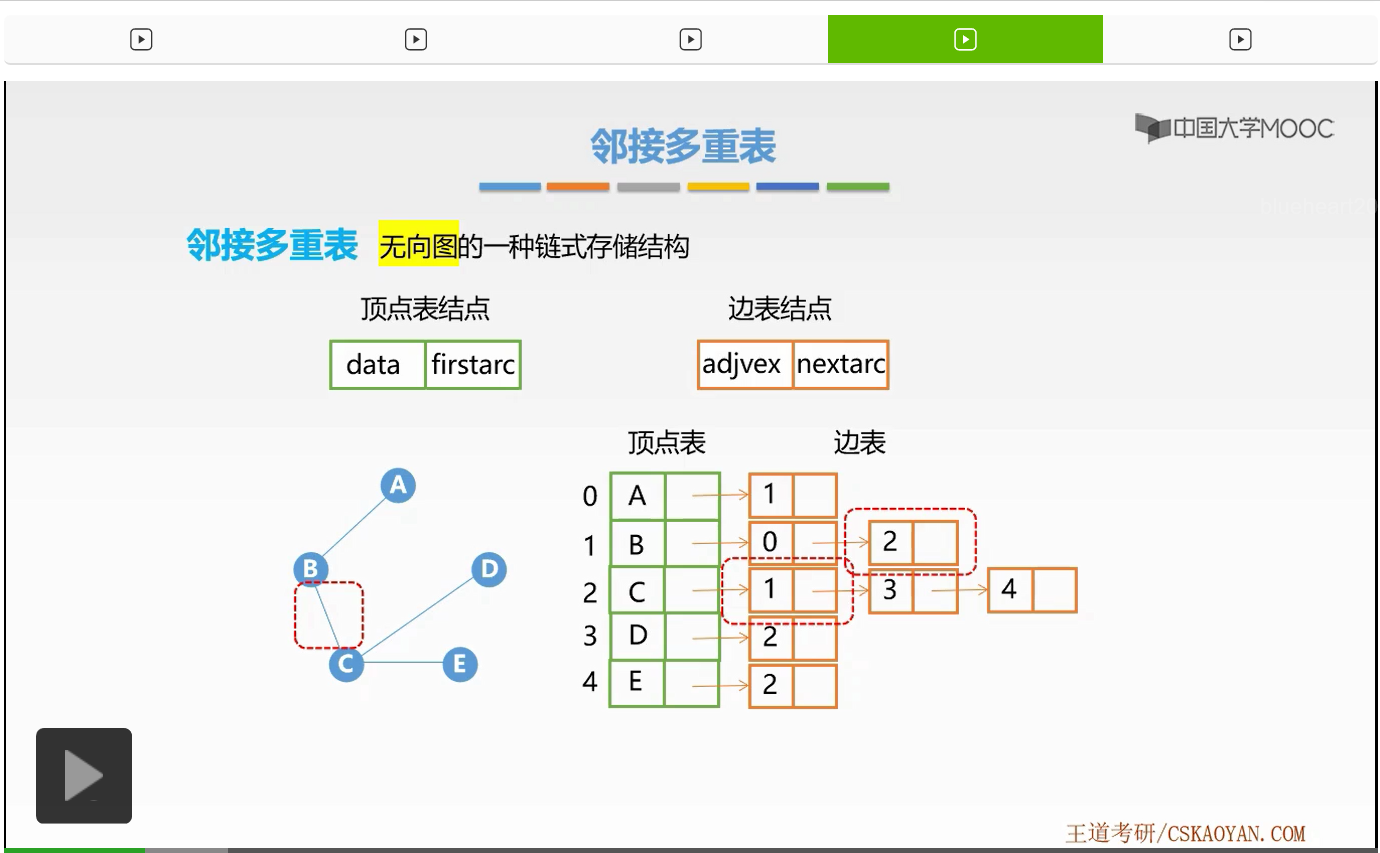
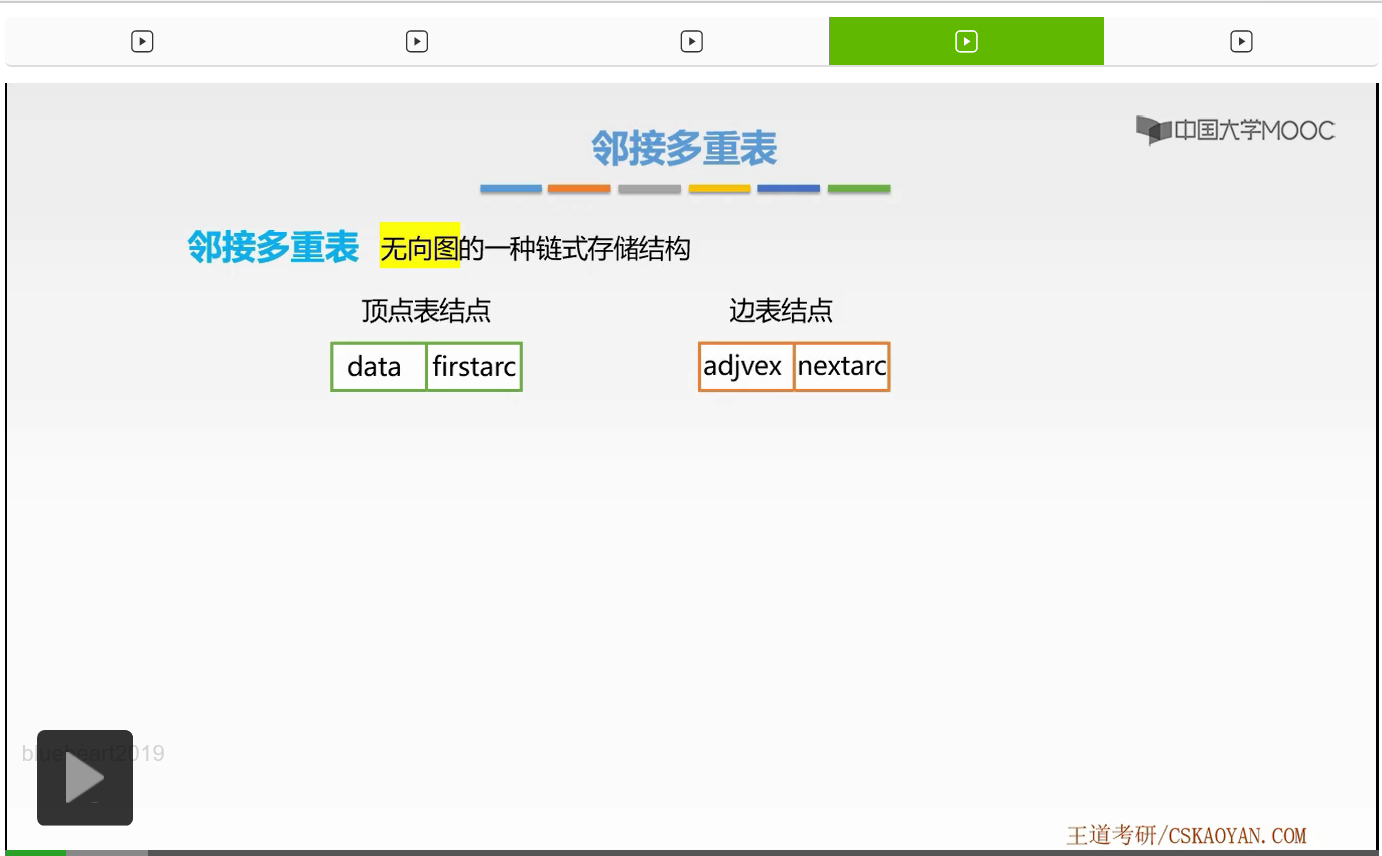
那么在邻接多重表法当中,依旧有两种表,第一种表也就是存放着顶点信息的顶点表,第二种表也就是存放着边关系的边表。我们首先来看顶点表结点。顶点表结点其实对它修改并不大,几乎是没有修改的。data域存放的依旧是保存数据的数据域data,第二部分依旧存放的是属于它的边表单链表的头指针,也就是第一个结点的指针firstedge。那么接下来我们来看一下,它的边表结点做出了哪些优化。那么边表结点的变化是比较大的,有这样6个域。我们来看一下这6个域分别表示的是什么,第一域表示的是该边的第一个端点,下一个域ilink表示的是与该端点相邻的下一个边的边表结点的指针。那么第三个域存放的则是第二个端点。而第四个域jlink存放的是第二个与端点相邻的下一个边的边表结点的指针。而最后两个域info和mark都是不是必要的域,那么我们如果有权重的话我们要增加info域表示权重。那么如果我们需要标记的话则要增加mark域,那么对该条边进行标记。这就是这样6个域。为什么要做出这样的优化呢?因为我们知道,每一条边都要有两个端点,那么这一条边既连接于第一个端点也连接于第二个端点。所以该边表结点当中,既要保存属于第一个端点的相关信息,也要保存属于第二个端点的相关信息。所以我们扩充了这些端点。好,这就是邻接多重表的顶点表结点以及边表结点的结构。
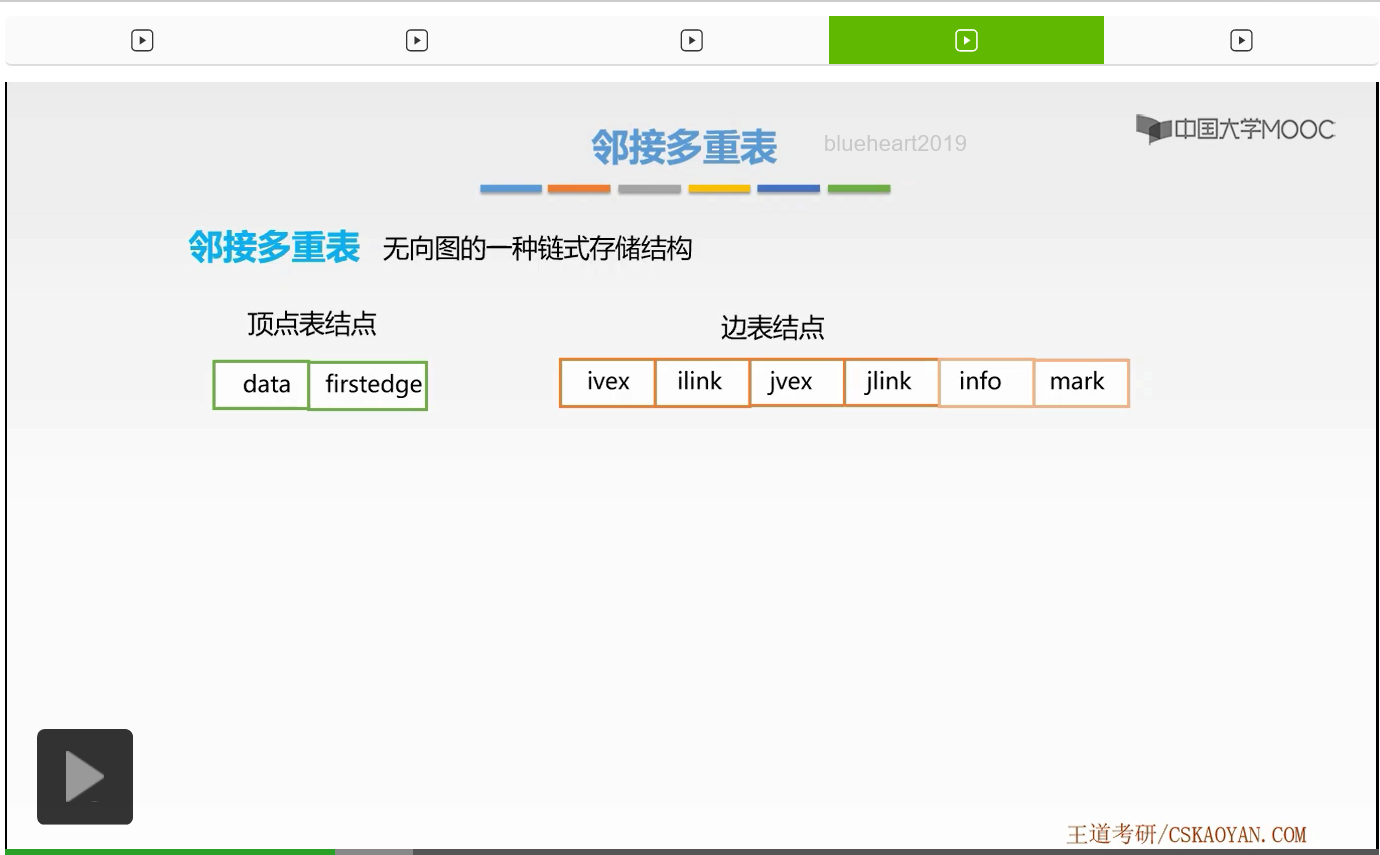
接下来我们来看一个例子。来看一下这些结点是如何组合在一起,形成一个邻接多重表的。那么这是一个无向图的例子。首先,我们还是来建立它的顶点表。因为该无向图有5个顶点,所以顶点表有5个顶点表结点依旧存放在数组当中。前面0-4是它的数组下标,首先我们来填放它的数据域部分,从A到E。接下来我们就来建立它的边表。那么首先我们来看A顶点,A顶点有这样一条无向边与它相邻,所以我们建立一个边表结点。那么这样边表结点因为它没有权重,也不需要标记,所以我们省略了info域和mark域。只有这样4个域,分别表示着第一个端点,第一个端点的指针,第二个端点,第二个端点的指针。

好,接下来我们就来看一下这些域是如何进行赋值的。首先,该条边的两个端点是A和B。那么A和B对应的数组下标就是0和1。所以我们将两个端点分别填放为0和填放为1。接着我们知道,该条边既连接于A顶点,也连接于B顶点,所以我们要将A和B顶点当中的指针域都指向该边表结点。好,这样我们就形成了第一个边表结点。接着我们来看下一条边。
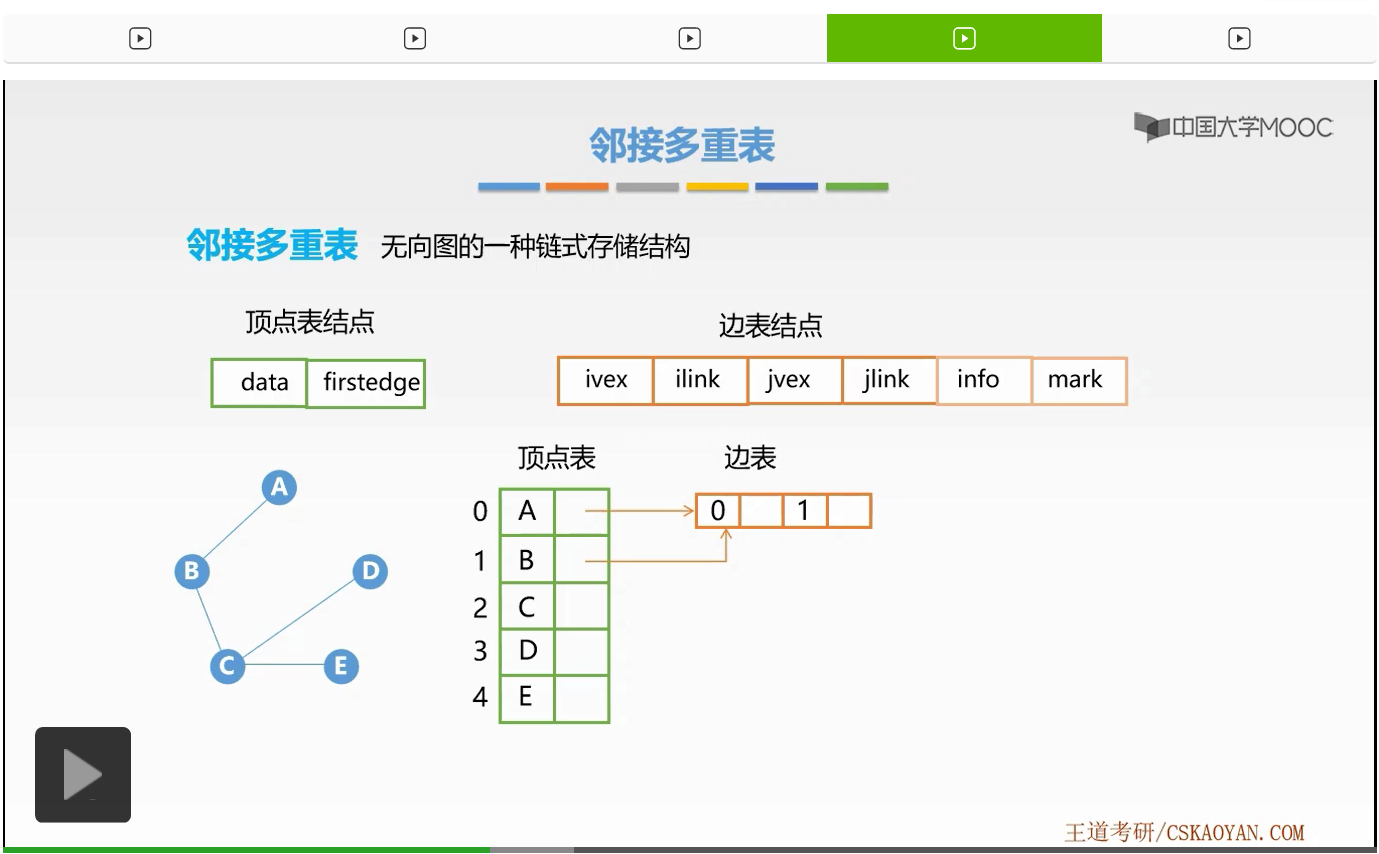
下一条边是BC这条无向边,那么我们依旧生成一个边表结点。那么这四个域应该如何进行填放呢?
本节课我们一起来学习有关图的基本操作。那么图在采用不同的存储结构,它具体操作的实现方式也会不同。所以我们还要分析一下图在采用邻接矩阵或者是邻接表之后它对基本操作的效率会产生哪些影响。
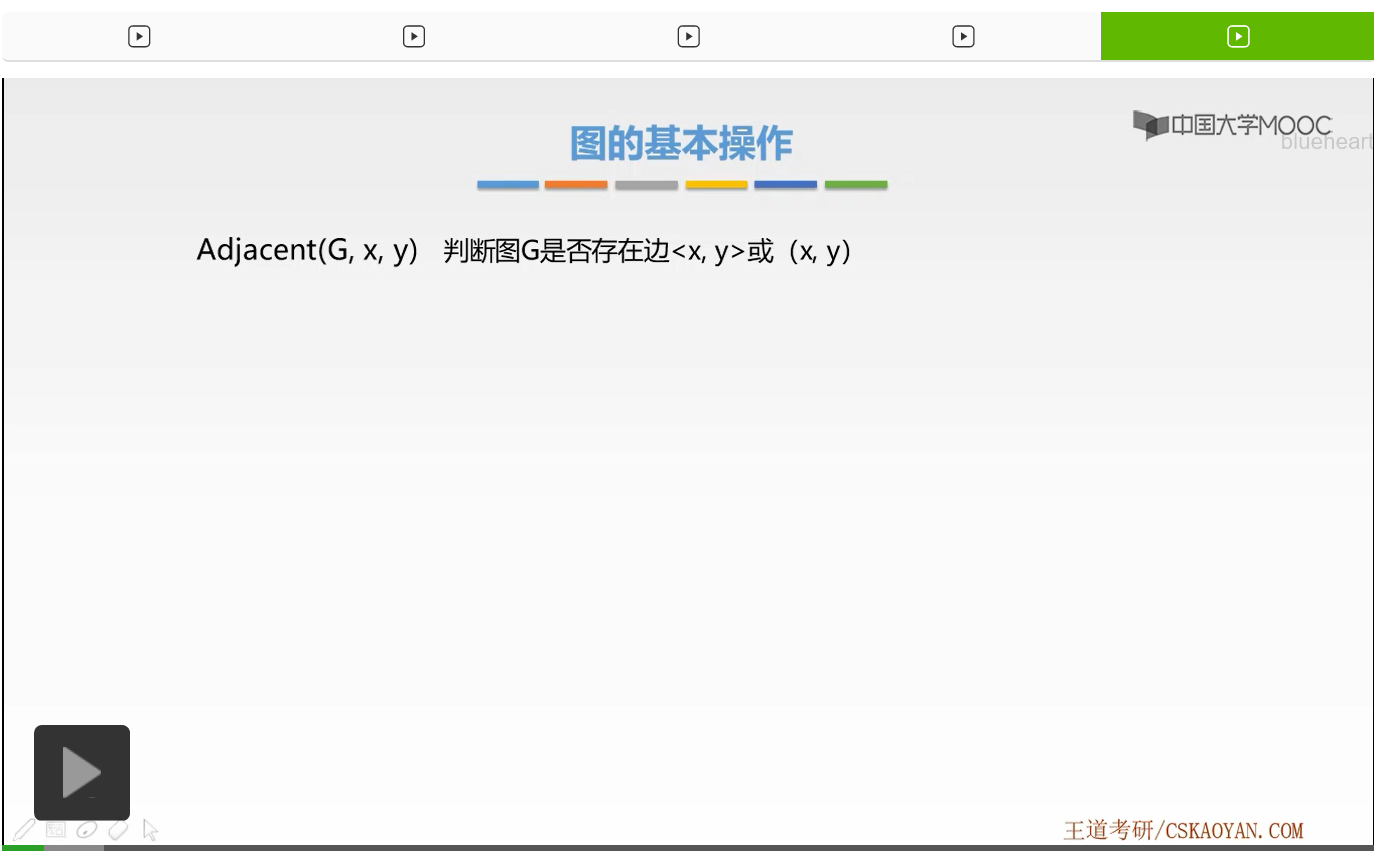
好,接下来我们来学习图的第一个操作Ajacent。它是判断图G是否存在这样一条边,一条无向边或者是一条有向边(x,y)。它传入参数有三个,分别是图G以及传入的两个参数两个端点。那么这里我们忽略了传入参数的类型。
首先我们来看一个无向图的例子。对于这样一个无向图,它采用邻接矩阵或者是邻接表时,它的具体实现会有哪些不同呢?
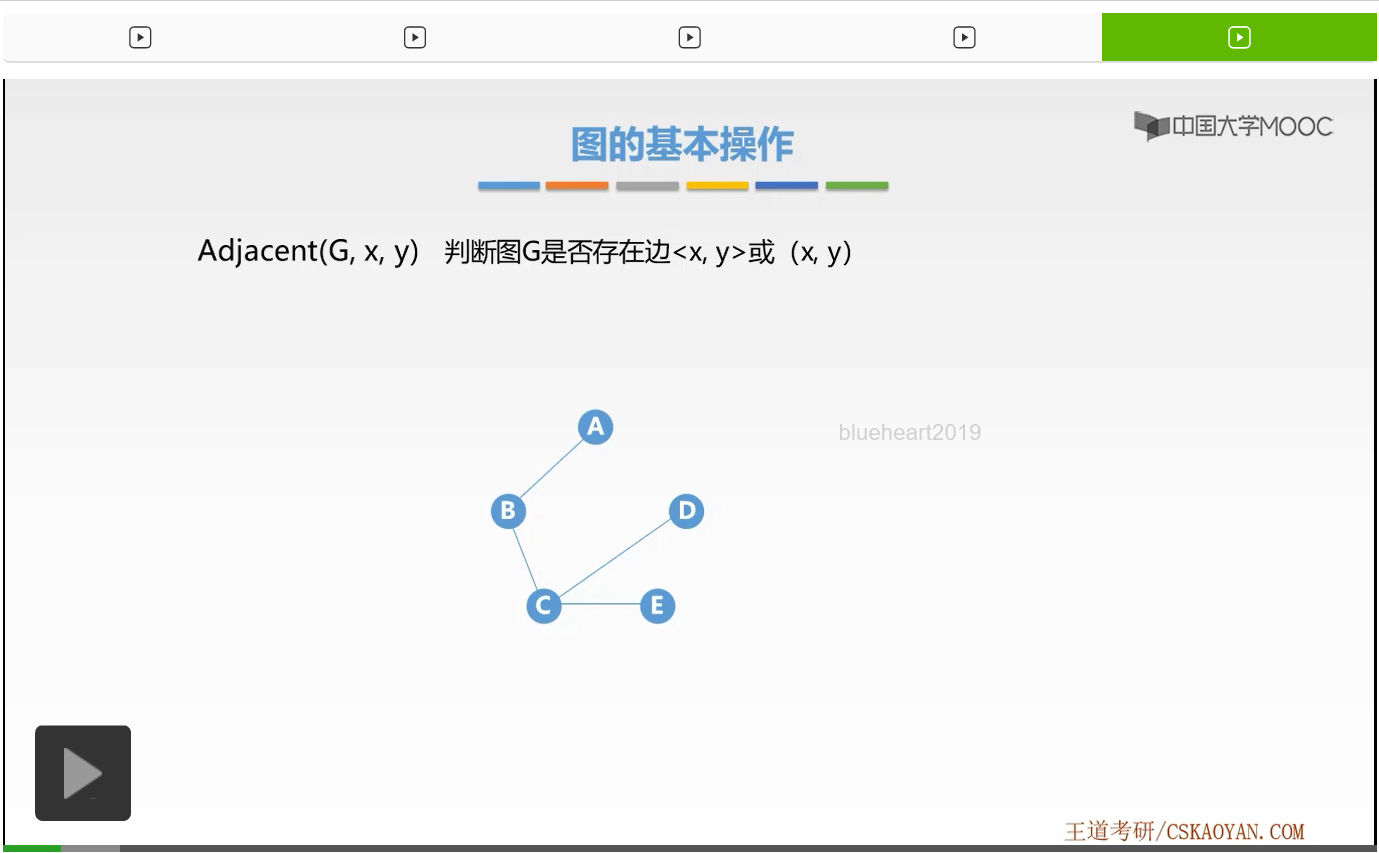
我们首先来看邻接矩阵表示法。那么这里我们写出了它的顶点表,其实对于许多题目来讲我们是忽略顶点表的,也就是说顶点仅仅只有编号并没有具体存放的数据。那么如果我们在做题时只看到了邻接矩阵,大家也不要陌生。

好,我们来看它的邻接表。那么这是该无向图的邻接表,依旧有顶点表以及边表。那么简单回忆一下,在邻接矩阵当中,其实对于无向图的存储来讲,它是一个对称矩阵。也就是说我们每一个无向边要用两个有向边的位置来表示。那么在邻接表中也是用两个边表结点来表示一条无向边。两个方向相反的有向边表示一条无向边,好,这就是它的邻接矩阵表示法以及它的邻接表表示法。那么接下来我们来看这样一个函数具体是如何实现的。在邻接矩阵表示法当中如果想要找到一条边是否存在,那么我们是不是找到对应邻接矩阵当中一个位置的值就可以啊。如果它是1就表示该边存在,如果它是0则表示该边不存在。在无向图当中我们有两个位置的值可以判断该边是否存在。那么在邻接表表示法当中,我们则要找到对应某一个顶点的边表当中是否存在这样一条边的边表结点。因为它是无向图,所以我们两个端点的边表结点都可以搜索到该边。好,这就是我们对应该函数的实现方式。

接下来我们来看一个这样的例子。



