【知识强化】第五章 图 5.1 图的基本概念

那么学习图这种数据结构与我们之前学习的方式是一样的,我们也要从三方面对它进行学习。首先是它的逻辑结构,以及一些相关的概念。接着是它的存储结构还有它的操作。那么接下来我们来看一下本章所要学习的主要知识点。首先我们会讲解图的逻辑结构及它一些相关的基本概念。接着我们会讲解图的存储结构。图的存储结构主要有四种,分别是邻接矩阵、邻接表法、邻接多重表以及十字链表。那么前两种表示方法是针对于顺序存储以及链式存储的,后两种方法是一种扩展,那么它们针对于有向图和无向图。这个我们之后会详细讲解。接着我们会讲有关图的遍历操作,对于图来讲的它的主要遍历方法有两种,第一种是广度优先遍历,第二种是深度优先遍历。我们会细节地讲解它的遍历过程以及它的算法实现。最后我们也要讲解图的一些相关重要应用。在考研当中,最重要的应用有四个,分别是最小生成树、最短路径、拓扑排序以及关键路径。好,这就是本章所要讲解的主要知识点。

那么本节课我们首先先来学习有关图的基本概念。
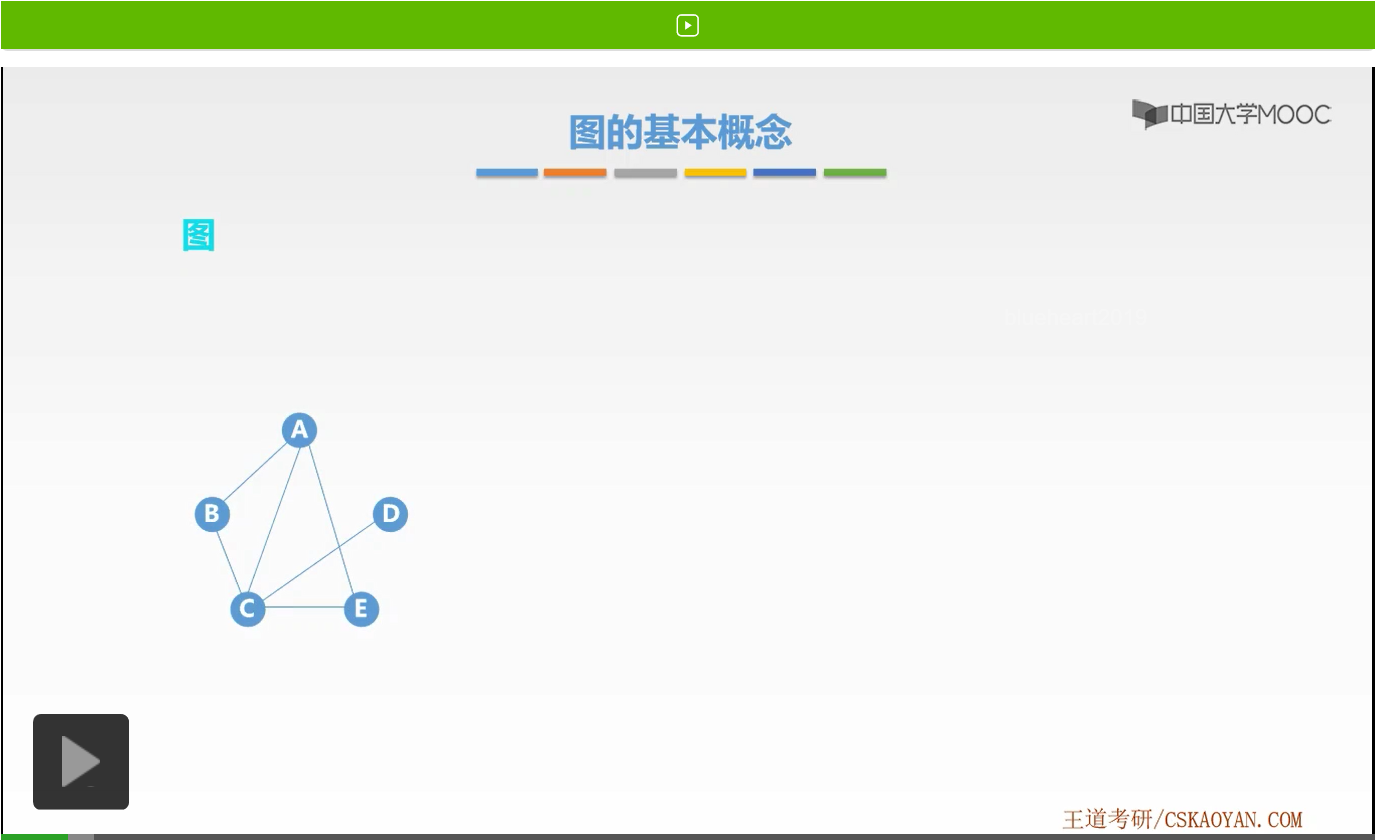
什么是图呢?之前我们学习过线性表这种线性结构它是一对一的关系,上一章我们讲解一个一对多的关系,一个非线性结构那就是树形结构。图是什么样的关系呢?在第一章我们学习过,图是多对多的关系。

也就是每一个结点都可以有许多结点与它相连。
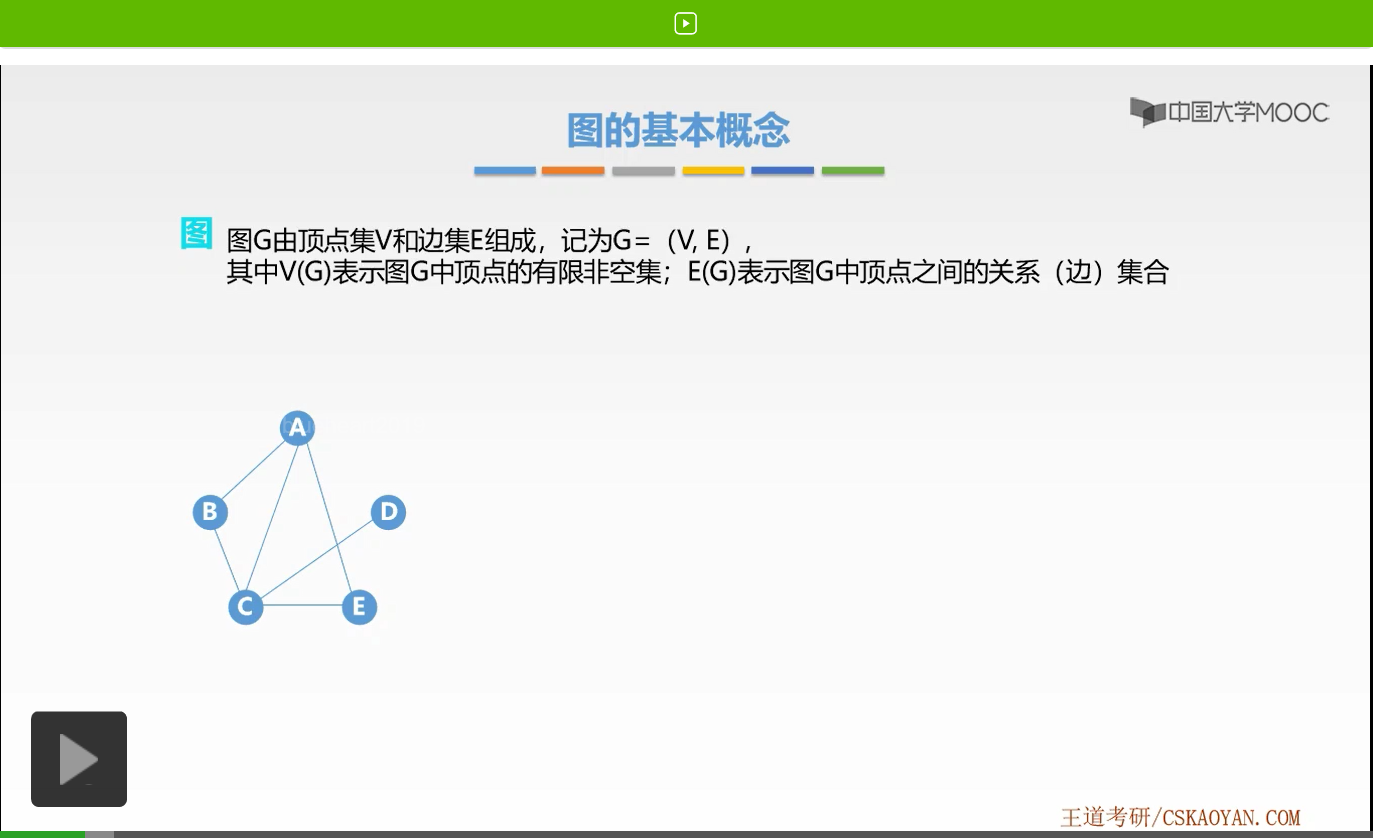
在书中对于图是如何定义的呢?书中是这样严格定义的。图G由顶点集V以及边集E组成,记为G=(V,E)。我们用这样的二元组,顶点集以及边集表示一个图G。接着它讲其中V(G)表示图G中顶点的有限非空集,E(G)表示图G中顶点之间关系集合,也就是我们所说的边的集合。
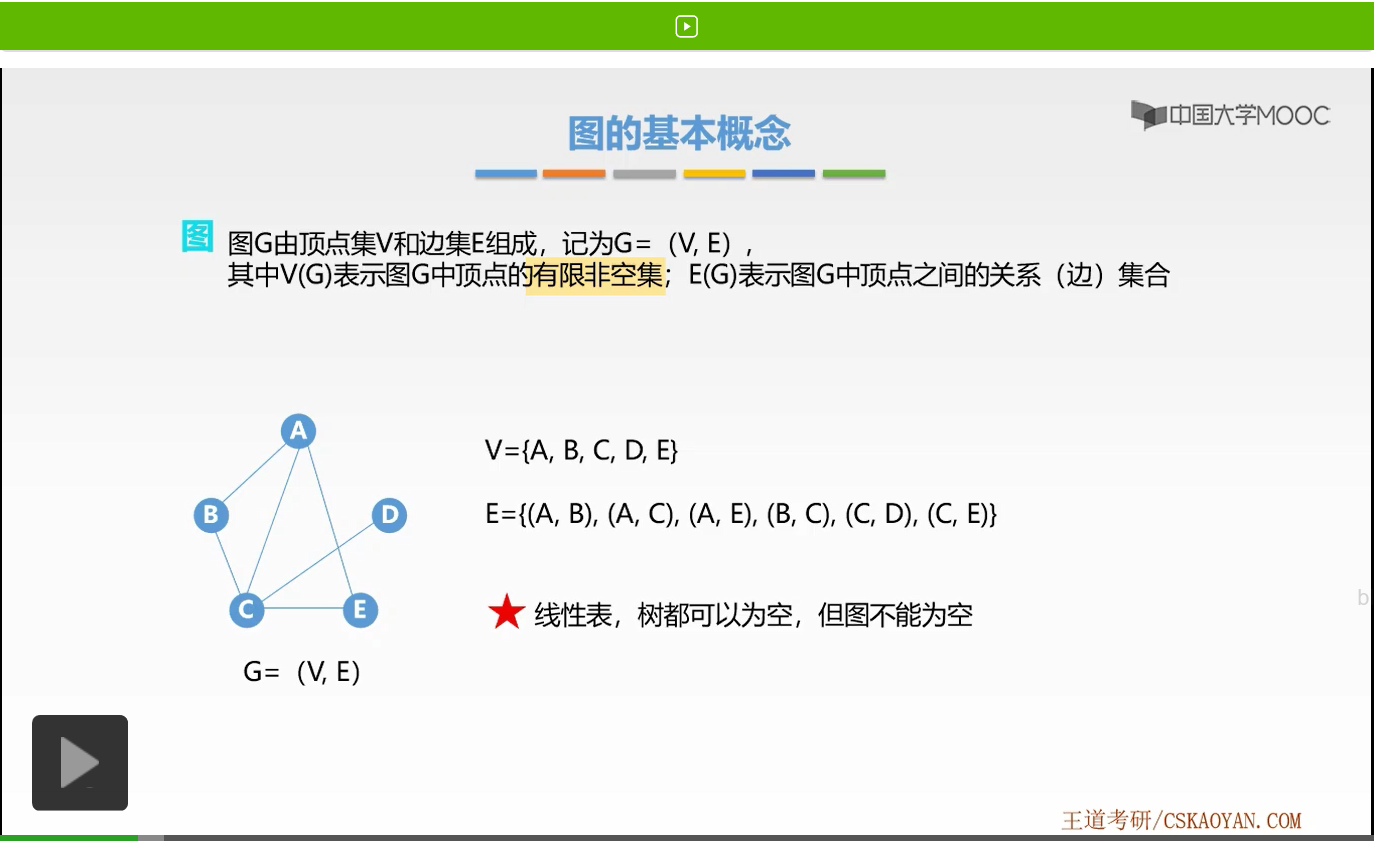
那么我们来看下面这个例子,假如它是一个图,它是G,由这样的二元组来表示。那么该图的顶点集怎样表示呢?我们用V大括号圈起了所有的顶点。那么在该图当中,一共有5个顶点,分别是A、B、C、D、E,我们用这样的方法表示了图的顶点集。

接着我们来看边集是如何表示的。边集依旧用一个大括号圈起了所有的边。那么每一个边是如何表示的呢?我们用一个小括号来表示了一条边,在小括号当中有两个字母,这两个字母表示了该条边的两个端点。那么这里为什么要用小括号呢?之后我们会有详细的讲解。好,这样我们就表示了边集。那么A、B这条边,我们就用了小括号A、B这样来表示。这就是边集的表示方法。

接下来我们来看,那么在定义当中有一个非常重要的点就是有限非空集,这里有限非空集为什么很重要呢?

因为它说明了图是不能为空的。大家回忆一下,在之前我们讲解过,线性表可以为空,树可以为空,但在这里图一定不能为空,没有空图这种表示方法。好,这就是定义当中我们要注意的一个点。
好接下来我们来看我们用绝对值符号,例如绝对值V表示图G中顶点的个数。用这种绝对值符号把集合



