【知识强化】第三章 栈和队列 3.1 栈

在第三章我们将继续学习三种非常重要的线性结构,分别是栈和队列的这样的受限线性表。我们将从它们的基本概念、存储结构以及相关应用这三方面进行详细的学习。最后我们将学习数组的相关知识,大家要注意一下这里的数组指的是一种线性结构,与我们之前在程序设计语言当中提到的数组类型是不同的概念。好,数组我们会学习它的定义以及它的存储结构,还有用数组来实现矩阵的压缩存储。最后还会提一个特殊的矩阵叫做稀疏矩阵。好,这就是本章所要学习的重要考点。本章所学习的知识点其实并不难,它常常出现在选择题当中,但是在之后我们解决一些算法时会经常用到本章所提到的数据结构以及在其他学科的学习过程当中我们也会有所应用,所以它是一个非常重要的基础知识。
好,本节课我们就先来学习栈的相关知识。首先来看栈的基本概念。
什么是栈呢?我们来看一个这样的小例子。我们在洗好盘子之后,都会这样依次地叠放。其实在这样一叠盘子当中,我们的操作是受限的。什么叫受限呢?我们无法从这些盘子中间的部分进行放入新盘的操作,以及拿出盘子的操作。我们只能在这些盘子的顶部进行放入新盘子的操作,以及拿走盘子的操作。这种操作就是我们刚刚所说的受限操作。其实它用接下来要学习的栈,有非常多的相似之处。

我们来看书中这样的定义。栈,英文名叫Stack,是一叠一堆的意思。书中是这样定义它的,只允许在一端进行插入或者删除操作的线性表。在定义当中我们只要注意两点,第一点是栈一定是线性表,它具有线性表的所有特点。第二点是它是受限线性表。怎样受限呢?是只允许在一端进行插入或者删除的线性表。好,这就是栈的定义。接下来我们用数据元素来代替盘子画出一个栈的例子。
这是一个空栈,其中没有任何的数据元素。当我们进行进栈操作时,我们只能在栈的顶部进行入栈。

而且每一次如果我们想要取走数据元素时,只能取走最顶部的数据元素进行出栈。

所有的入栈、出栈操作只有在栈的顶部才能进行,这样我们就画出了一个栈S。

我们称可以进行出栈、入栈操作那一边为栈顶,其中a5为这里的栈顶元素。而无法进行出栈、入栈操作那一边称为栈底,这里a1为栈底元素。我们发现该栈的入栈序列为,a1、a2、a3、a4、a5。而弹栈时我们只能选择栈顶元素进行出栈。所以它的出栈序列为a5、a4、a3、a2、a1,刚刚好是反过来的。在栈中先进入栈的元素会后进行出栈,所以栈是一个后进先出的数据结构。在后面的学习过程当中我们会利用栈这样后进先出的特点解决许多算法问题。好,这就是有关栈的基本概念。

接下来我们来介绍一下栈的基本操作。首先是一个初始化栈的操作。它初始化了一个空栈S,叫InitSack。接下来是一个判断栈是否为空的操作,若栈为空,则返回true。否则,返回false。好,接下来就是两个非常重要操作,一个是Push操作,它是进栈。第二个是Pop操作,它是出栈。其实这两操作的取名非常形象,Push就是压的意思,Pop就是弹出的意思。Push操作传入的参数有两个,一个是操作栈的引用,第二个是进栈的元素x。进栈操作一定要事先判断栈是否已经满了,若满了则无法进栈,若未满则将x加入使之成为新的栈顶。接下来Pop操作的传入参数也就有两个,一个是操作栈的引用,第二个是保存弹出元素的引用x。出栈操作也需要事先判断,如果栈非空才可以弹出栈的元素,并用x返回。若栈为空,则无法弹出元素。接下来我们来看GetTop操作,GetTop的作用是返回栈顶元素。这里我们发现Pop操作也可以返回栈顶元素,但是它们之间是有非常大的区别的。因为Pop在返回栈顶元素的同时,也会删除栈顶元素,而GetTop则不会。GetTop传入参数是一个栈S以及保存栈顶元素引用x。我们发现,因为这里我们没有删除栈顶元素,所以传入参数x是没有用引用的。好,接下来我们来看最后一个操作就是清除栈操作,销毁栈,ClearStack,传入的是一个栈的引用。销毁栈,并释放S所占用的内存空间。这就是栈的所有基本操作。这里与线性表一样,我们也只是简单介绍各个函数的功能,在接下来我们确定了栈的存储结构时,我们才会具体地实现它。好,这就是本节课的所有内容。

上一节课我们学习了栈的逻辑结构,与线性表相同,接下来我们也会讲述栈的两种存储方式,分别是顺序存储结构与链式存储结构。本节课我们就先来学习栈的顺序存储结构。
经过上节课的学习我们知道,栈是一种受限的线性表。那么在学习栈的顺序存储结构之前,我们先来复习一下顺序表也就是线性表的顺序存储结构。我们知道顺序表当中,每一个逻辑上相邻的数据元素在物理上也是相邻存放的,而且它是通过数组来实现。那么其实栈也有这样的特点,但是栈是一种受限的线性表。
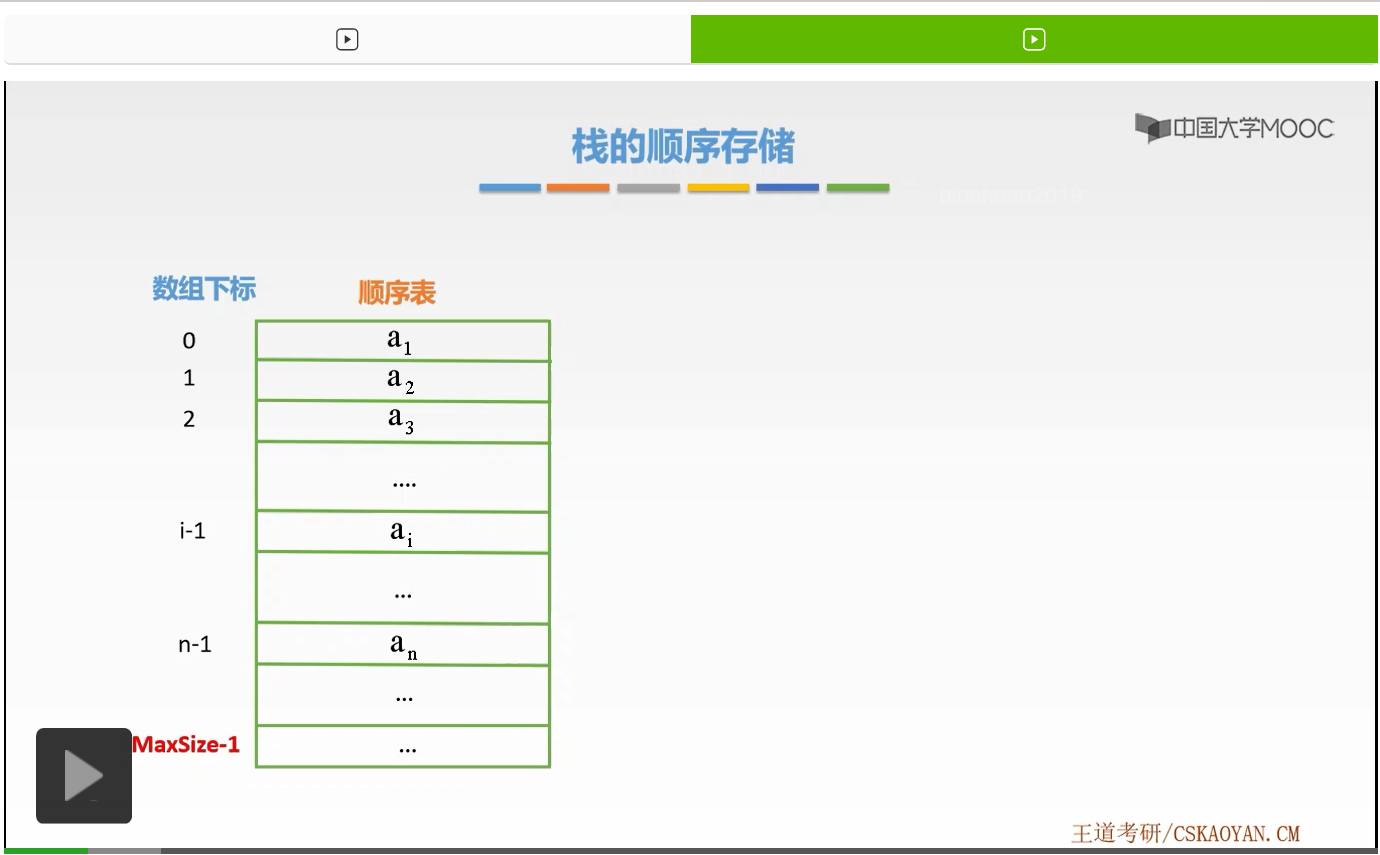
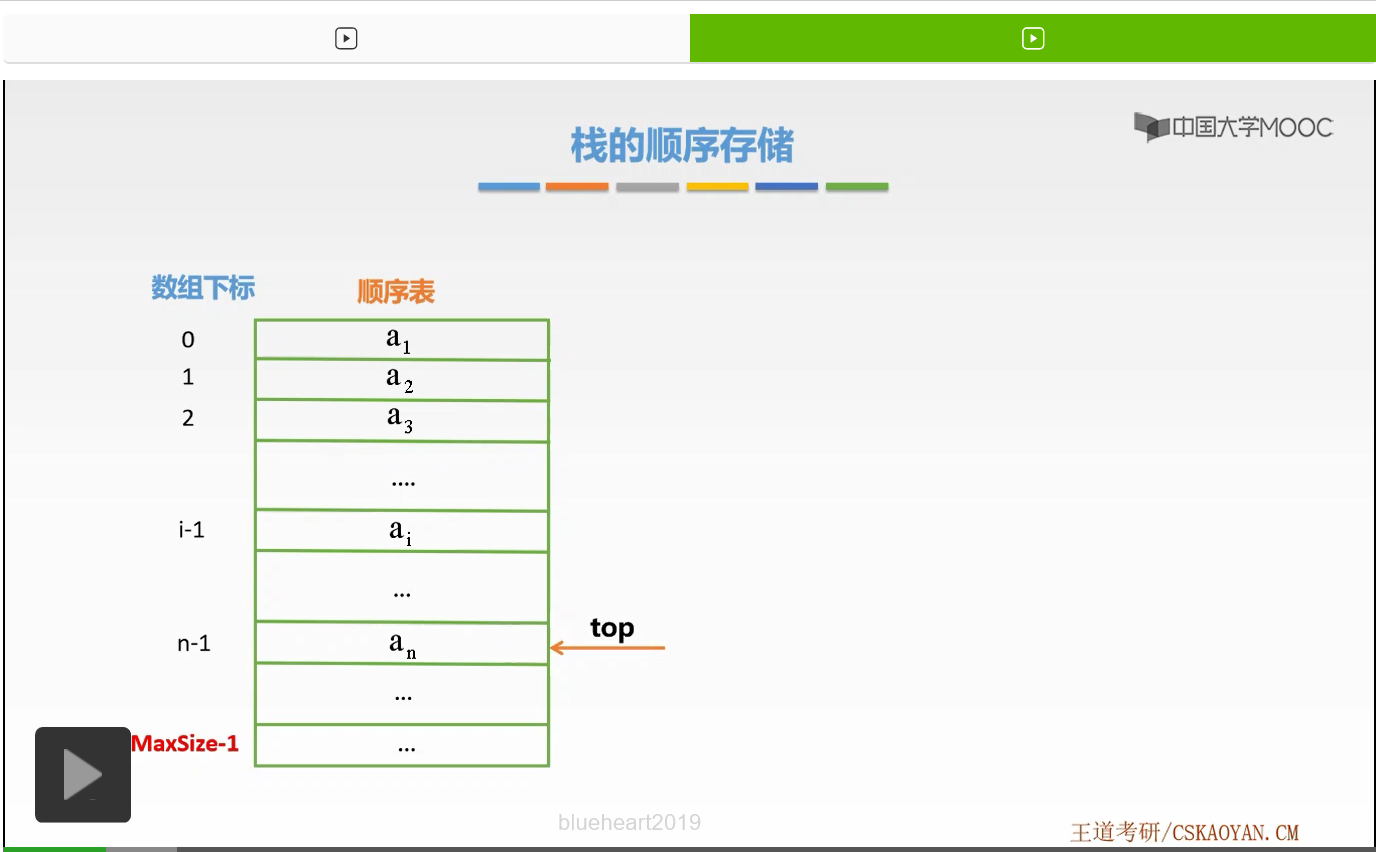
那么怎么样体现这个受限的操作呢,我们利用了一个指向栈顶的指针Pop来标识我们进行受限操作的位置,也就是弹栈和入栈的位置。
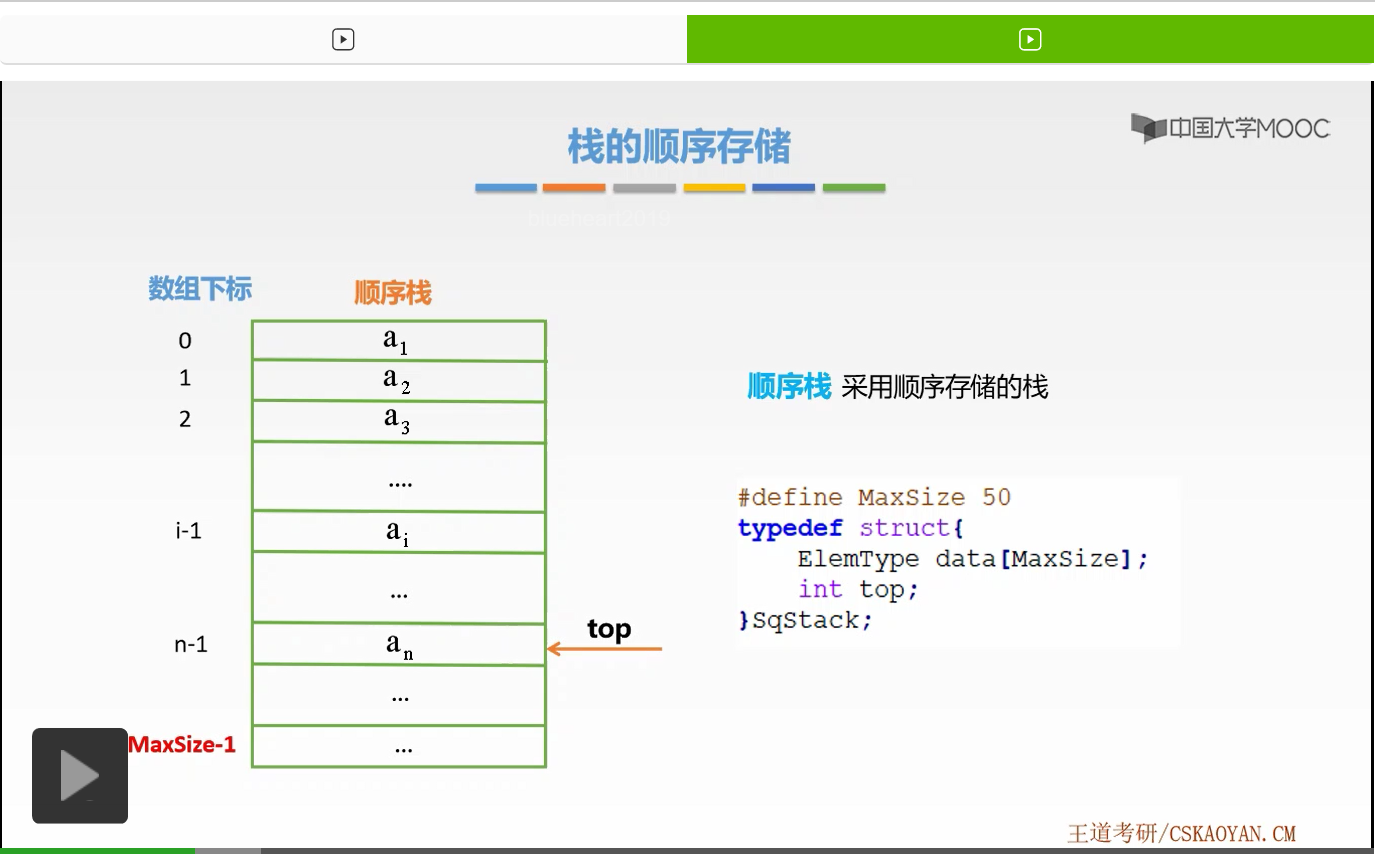
那么其实栈的定义也非常的简单,它就是采用顺序存储的栈。那么在程序设计语言当中,栈是如何来实现的呢?其实它也是通过一个结构体来实现的。与顺序表非常的相似,也是首先定义了数组的大小,在结构体当中也有两个元素。第一个是存放数据元素的数组,第二个是指向栈顶元素的指针。它是通过一个整型变量top来实现的,标识了可以进行弹栈和压栈操作的位置,也就是数组的下标。在该结构体当中,我们发现它与顺序表不同,没有了标识顺序表长度的变量Length,而是只有指向栈顶元素的指针top。那么这样我们应该如何求算顺序栈数据元素的数量呢,以及如何判断栈空或者是栈满呢?
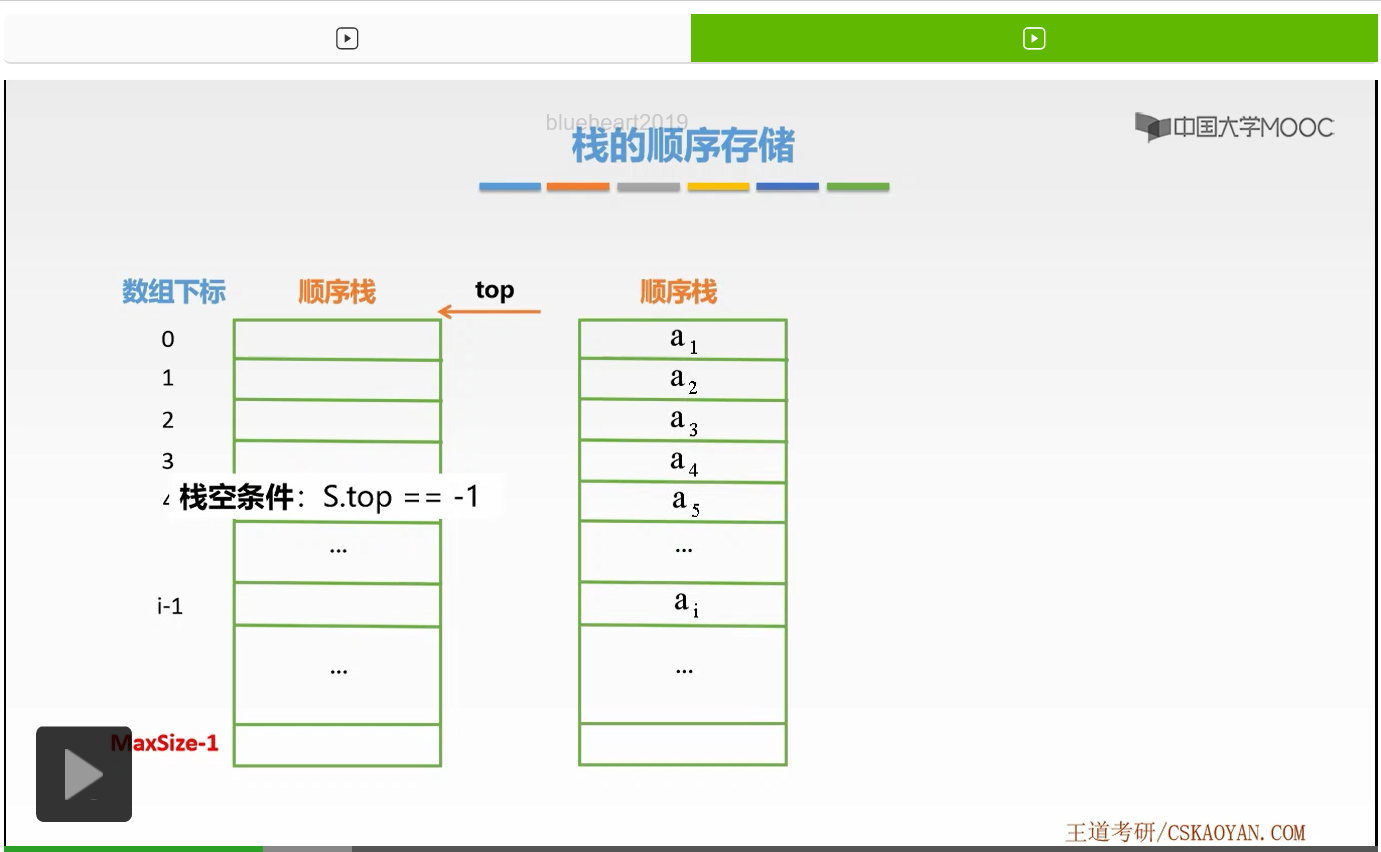
我们首先来看如何判断栈空。这是一个顺序栈,它里面没有任何元素。那么此时top指针应该指向什么样的位置呢?
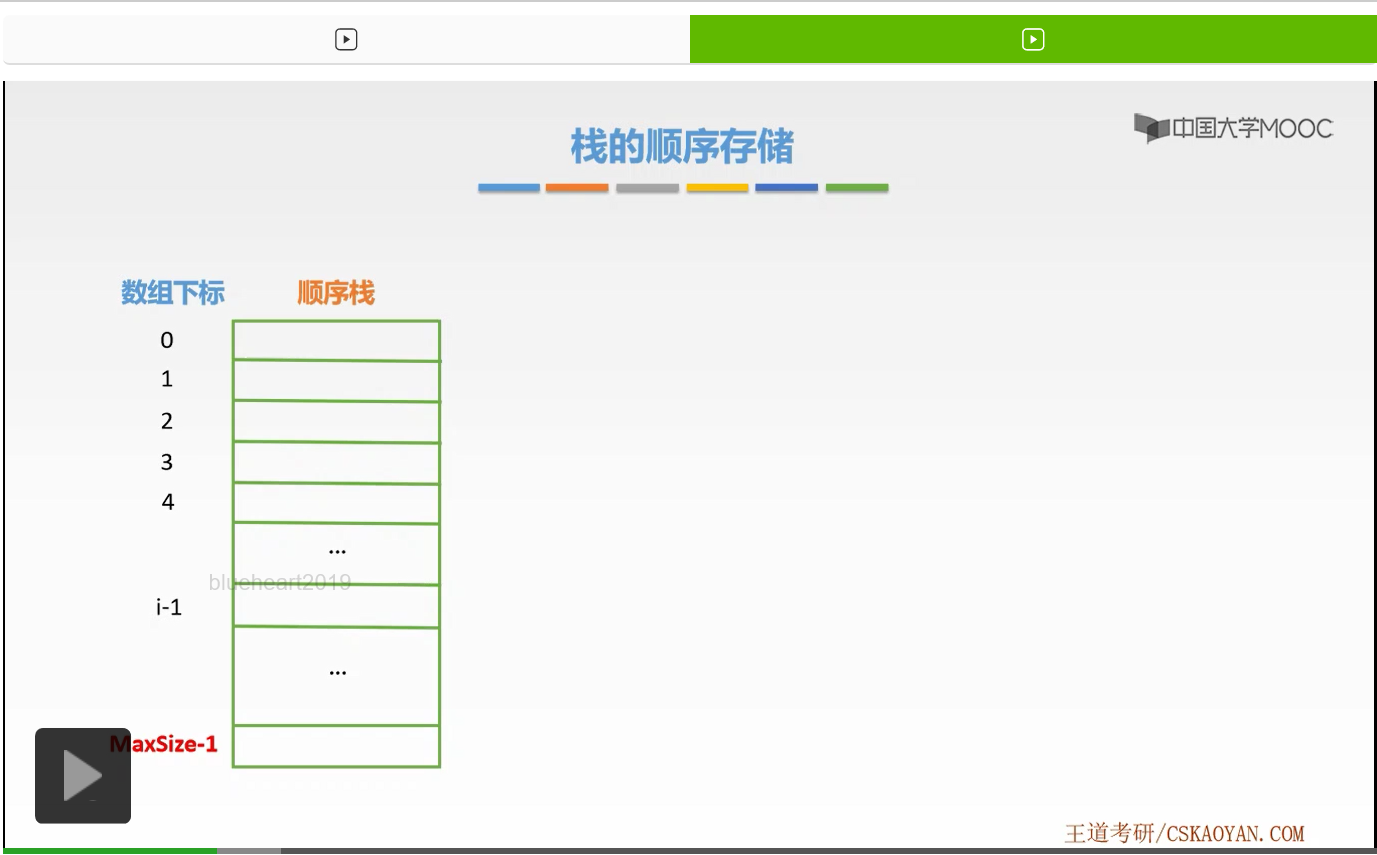
因为它没有任何元素,也就是即使在数组0下标下的位置也是没有元素的。

所以判断栈空条件是S.top==-1。当=-1时,就说明这个顺序栈没有任何数据元素。

接下来我们就来学习如何求算顺序栈的长度。我们知道在顺序栈当中每一个数据元素是连续存放的,
而且top指针指向了数组下标最大的那个数据元素。所以我们可以利用top来求算顺序栈的长度。
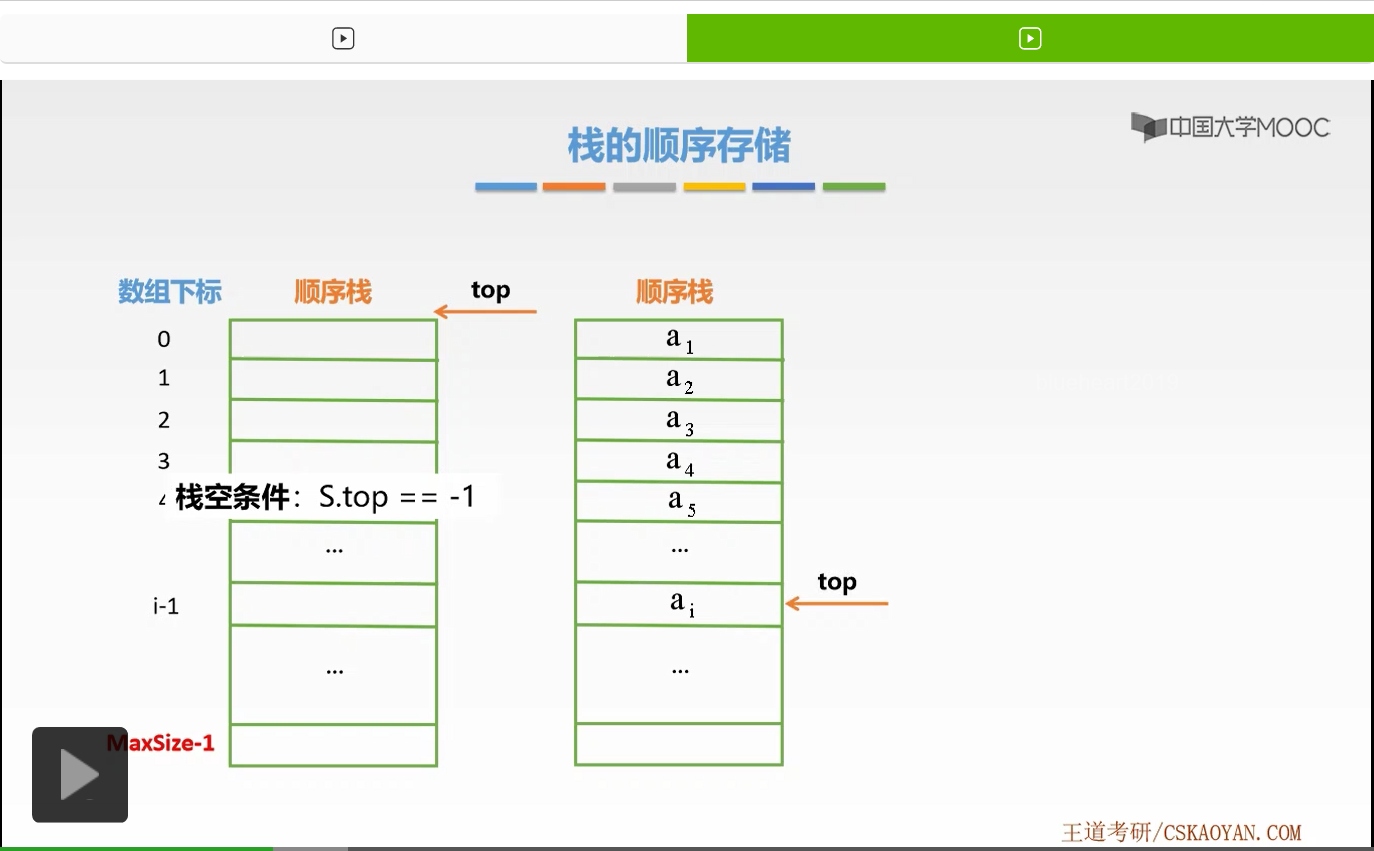
怎样求算呢?顺序栈的栈长等于S.top+1。这里为什么要加1啊,数组下标是从0开始的,而顺序栈的元素标号是从1开始的,



