Luogu3768简单的数学题

题目描述

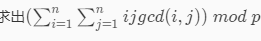
题解

我们在一通化简上面的式子之后得到了这么个东西。

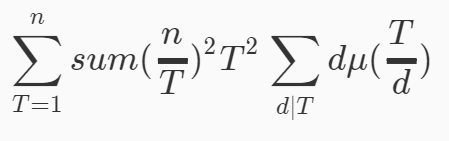
前面的可以除法分块做，后面的∑T²∑dµ(T/d)是积性函数，可以线性筛。

然后这个数据范围好像不太支持线性筛，所以考虑杜教筛。

后面那个东西是个id*µ,恰好等于φ。

所以我们求得东西就变成了i²φ。

由于φ*I=id。所以我们令g(i)=i²,f(x)=i²φ,f*g=i³

于是这道题就做完了。

附：1^2+2^2+3^2+...+n^2=n*(n+1)*(2*n+1)/6，1^3+2^3+...+n^3=(1+2+3+..+n)^2。

代码

#include<iostream>
#include<cstdio>
#include<map>
#define N 5000009 
using namespace std;
typedef long long ll;
map<ll,ll>mp;
const int maxn=5000000;
ll mod,ans,inv2,inv6,k,phi[N],n;
int prime[N];
bool vis[N];
inline ll rd(){
    ll x=0;char c=getchar();bool f=0;
    while(!isdigit(c)){if(c=='-')f=1;c=getchar();}
    while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return f?-x:x;
}
inline ll power(ll x,ll y){
    ll ans=1;
    while(y){if(y&1)ans=ans*x%mod;x=x*x%mod;y>>=1;}
    return ans;
}
inline void prework(){
    ll k;
    phi[1]=1;
    for(int i=2;i<=maxn;++i){
        if(!vis[i]){prime[++prime[0]]=i;phi[i]=i-1;}
        for(int j=1;j<=prime[0]&&(k=i*prime[j])<=maxn;++j){
            vis[i*prime[j]]=1;
            if(i%prime[j]==0){phi[i*prime[j]]=phi[i]*prime[j];break;}
            else phi[i*prime[j]]=phi[i]*phi[prime[j]];
        }
    }
    for(int i=1;i<=maxn;++i)phi[i]=(phi[i]*i%mod*i%mod+phi[i-1])%mod;
}
inline ll sum(ll x){return x%mod*(x+1)%mod*inv2%mod;}
inline ll pf(ll x){return x%mod*x%mod;}
inline ll pfsum(ll x){return x%mod*(x+1)%mod*(2*x%mod+1)%mod*inv6%mod;}
ll get_phi(ll n){
    if(n<=maxn)return phi[n];
    if(mp.find(n)!=mp.end())return mp[n];
    ll ans=pf(sum(n));ll r;
    for(ll l=2;l<=n;l=r+1){
        r=n/(n/l);
        ll x=((pfsum(r)-pfsum(l-1))%mod+mod)%mod;
        ans=(ans-x*get_phi(n/l)%mod+mod)%mod;
    }
    return mp[n]=ans;
}
int main(){
    mod=rd();n=rd();
    inv2=power(2,mod-2);inv6=power(6,mod-2);
    prework();
    ll l,r;
    for(l=1;l<=n;l=r+1){
        r=n/(n/l);
        ans+=pf(sum(n/l))*(get_phi(r)-get_phi(l-1))%mod;
        ans=(ans%mod+mod)%mod;
    }
    cout<<ans;
    return 0; 
}