#46. 【清华集训2014】玄学

题目描述

http://uoj.ac/problem/46

题解

看起来像是个二维平面上%*￥￥……一下，实则不然。

麻烦一点的话我们可以对时间轴开一颗线段树，在线段树上的每一个节点上再开一颗线段树表示在这个操作范围内的修改操作和。

这样我们可以修改log^2查询log^2的完成。

然而修改是区间修改，查询是单点查询，需要下传标记，数组根本开不下，UOJ上只能过2个点。

#include<iostream>
#include<cstdio>
#define N 100009
using namespace std;
typedef long long ll;
const int maxn=100000;
int ls[N*100],rs[N*100],now,ans,n,m,a[N],tott,T[N<<2];
inline int rd(){
    int x=0;char c=getchar();bool f=0;
    while(!isdigit(c)){if(c=='-')f=1;c=getchar();}
    while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return f?-x:x;
}
struct node{
    int x,y;
    node(int xx=1,int yy=0){x=xx;y=yy;}
    inline bool size(){return x!=1||y!=0;}
    inline void clear(){x=1;y=0;} 
    node operator *(const node &b)const{return node{1ll*x*b.x%m,(1ll*b.x*y%m+1ll*b.y)%m};}
}tr[N*100];
inline void pushdown(int cnt){
    if(!ls[cnt])ls[cnt]=++tott;
    if(!rs[cnt])rs[cnt]=++tott;
    tr[ls[cnt]]=tr[ls[cnt]]*tr[cnt];tr[rs[cnt]]=tr[rs[cnt]]*tr[cnt];
    tr[cnt].clear();
}
void upd2(int &cnt,int l,int r,int L,int R,int x,int y){
    if(!cnt)cnt=++tott;
    if(l>=L&&r<=R){
        tr[cnt]=tr[cnt]*node{x,y};
        return;
    }
    if(tr[cnt].size())pushdown(cnt);
    int mid=(l+r)>>1;
    if(mid>=L)upd2(ls[cnt],l,mid,L,R,x,y);
    if(mid<R)upd2(rs[cnt],mid+1,r,L,R,x,y);
}
void upd(int cnt,int l,int r,int L,int R,int x,int y){
    upd2(T[cnt],1,n,L,R,x,y);
    if(l==r)return;
    int mid=(l+r)>>1;
    if(now<=mid)upd(cnt<<1,l,mid,L,R,x,y);
    else upd(cnt<<1|1,mid+1,r,L,R,x,y);
}
void query2(int &cnt,int l,int r,int x){
    if(!cnt)return;
    if(l==r){ans=(1ll*ans*tr[cnt].x%m+1ll*tr[cnt].y)%m;return;}
    if(tr[cnt].size())pushdown(cnt);
    int mid=(l+r)>>1;
    if(mid>=x)query2(ls[cnt],l,mid,x);
    else query2(rs[cnt],mid+1,r,x);
}
void query(int cnt,int l,int r,int L,int R,int x){
    if(l>=L&&r<=R){query2(T[cnt],1,n,x);return;}
    int mid=(l+r)>>1;
    if(mid>=L)query(cnt<<1,l,mid,L,R,x);
    if(mid<R)query(cnt<<1|1,mid+1,r,L,R,x);
}
int main(){
    int id=rd();id=id&1;
    n=rd();m=rd();
    for(int i=1;i<=n;++i)a[i]=rd();
    int x,y,k,u,v;int q=rd();
    while(q--){
        int opt=rd();
        if(opt==1){
            x=rd();y=rd();u=rd();v=rd();x^=id*ans;y^=id*ans;
            now++;
            upd(1,1,maxn,x,y,u,v); 
        }
        else{
            x=rd();y=rd();k=rd();x^=id*ans;y^=id*ans;k^=id*ans;
            ans=a[k];
            query(1,1,maxn,x,y,k);
            printf("%d\n",ans);
        }
    }
    return 0;
} 

正解非常巧妙，我们对于一个修改区间(l,r)，分别开三个修改，第一维为修改的r，第二维和第三维为修改的参数，为：(l-1,1,0)(r,1,0)(n,1,0)

这样，当查询点在l前面是，我们可以二分找到第一个r大于等于自己的修改，这样保证在任意位置都能查到正确的修改。

那么对于两组修改，我们可以用归并排序的方式把它们归并起来。

归并的时候，r需要去min，此时r的意思是所有位置最小是r的答案。

这里的归并就用到了二进制分组的思想。

假设当前有3个操作。

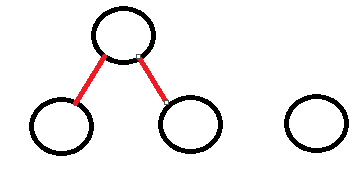
我们可以再去添加一个操作。

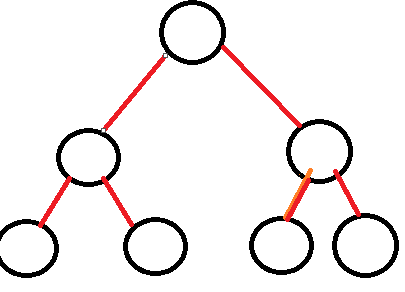
这样就把所有满二进制位的地方都归并起来了。

这个操作可以用线段树维护。

查询就找到对应节点二分一下就可以了。

代码

#include<iostream>
#include<cstdio>
#define N 100009
using namespace std;
typedef long long ll;
const int maxn=100000;
int tot,ls[N<<2],rs[N<<2],now,ans,n,m,a[N];
inline int rd(){
    int x=0;char c=getchar();bool f=0;
    while(!isdigit(c)){if(c=='-')f=1;c=getchar();}
    while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return f?-x:x;
}
struct node{int r,x,y;}st[N*50];
void upd(int cnt,int l,int r,int L,int R,int x,int y){
    if(l==r){
        ls[cnt]=tot+1;
        if(L>1)st[++tot]=node{L-1,1,0};
        st[++tot]=node{R,x,y};
        if(R<n)st[++tot]=node{n,1,0};
        rs[cnt]=tot;
        return;
    }
    int mid=(l+r)>>1;
    if(now<=mid)upd(cnt<<1,l,mid,L,R,x,y);
    else upd(cnt<<1|1,mid+1,r,L,R,x,y);
    if(now<r)return;
    ls[cnt]=tot+1;
    int l1=ls[cnt<<1],r1=rs[cnt<<1],l2=ls[cnt<<1|1],r2=rs[cnt<<1|1];
    while(l1<=r1&&l2<=r2){
        st[++tot]=node{min(st[l1].r,st[l2].r),1ll*st[l1].x*st[l2].x%m,(1ll*st[l1].y*st[l2].x%m+1ll*st[l2].y)%m};
        if(st[l1].r==st[l2].r)l1++,l2++;
        else if(st[l1].r<st[l2].r)l1++;else l2++;
    }
    rs[cnt]=tot;
}
inline void work(int cnt,int x){
    int l=ls[cnt],r=rs[cnt],nowans=0;
    while(l<=r){
        int mid=(l+r)>>1;
        if(st[mid].r>=x)nowans=mid,r=mid-1;else l=mid+1;
    }
    ans=(1ll*ans*st[nowans].x%m+1ll*st[nowans].y)%m;
}
void query(int cnt,int l,int r,int L,int R,int x){
    if(l>=L&&r<=R){work(cnt,x);return;}
    int mid=(l+r)>>1;
    if(mid>=L)query(cnt<<1,l,mid,L,R,x);
    if(mid<R)query(cnt<<1|1,mid+1,r,L,R,x);
}
int main(){
    int id=rd();id=id&1;
    n=rd();m=rd();
    for(int i=1;i<=n;++i)a[i]=rd();
    int x,y,k,u,v;int q=rd();
    while(q--){
        int opt=rd();
        if(opt==1){
            x=rd();y=rd();u=rd();v=rd();x^=id*ans;y^=id*ans;
            now++;
            upd(1,1,maxn,x,y,u,v); 
        }
        else{
            x=rd();y=rd();k=rd();x^=id*ans;y^=id*ans;k^=id*ans;
            ans=a[k];
            query(1,1,maxn,x,y,k);
            printf("%d\n",ans);
        }
    }
    return 0;
}