[Code+#3]寻找车位

题目描述

access_globe 有一个巨大的停车场，这个停车场有 $个车位。为了美观，access_globe 在建立这个停车场时，规定这个停车场必须是长条形的，即 n≥m。每个车位都是一个正方形的区域。$

最近，access_globe 正在为抽不到 Missing Poster 而苦恼，因此他请你帮他维护这个停车场。你需要支持两个个事件：

一辆车停到某一个车位中，或一辆车从某个车位开走
查询一个矩形区域内最大的只包含空车位的正方形区域

如果你能帮 access_globe 高效地解决这个问题，access_globe 一定会好好奖励你的

题解

因为n>m所以我们发现m其实是不大的，所以我们可以稍微放宽复杂度，qmlogn就可以了。

我们可以用线段树去维护每一行的值，一个upmax，一个downmx，一个mx。

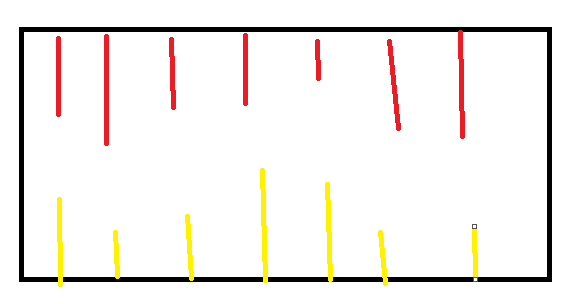
upmx就是从上面往下数最长一段连续的1也就是黄色部分，downmx为红色部分。

mx表示这个子矩形中最大的全1矩阵。

然后我们可以利用子树合并来维护这三个数组。

维护方法：用两个单调队列储存边界信息。

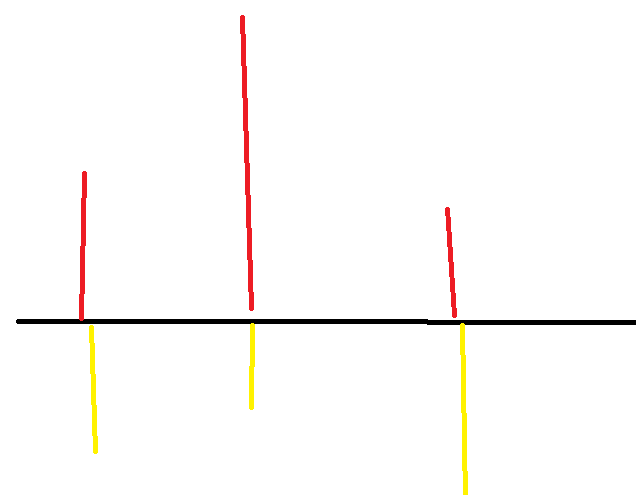
然后维护一个指针p来维护最大子矩形的上边界。

这样修改就好说了。

那么对于一个询问，它的边界不是1~m怎么办？

我们还可以O(m)的做一遍，对于每个节点储存的最大子矩形，我们卡一下边界就好了。

代码

#include<iostream>
#include<cstdio>
#define N 4000009
using namespace std;
int n,m,q1[N],q2[N],ans,now;
inline int rd(){
    int x=0;char c=getchar();bool f=0;
    while(!isdigit(c)){if(c=='-')f=1;c=getchar();}
    while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return f?-x:x;
}
struct node{
    int a[N<<2];
    int* operator[](int x){return a+x*m;}
}upmx,downmx,sum,a;
void merge(int cnt,int l,int r,int len1,int len2){
     int h1=1,h2=1,t1=0,t2=0,p=l;
     for(int i=l;i<=r;++i){
         while(h1<=t1&&downmx[cnt<<1][i]<downmx[cnt<<1][q1[t1]])t1--;q1[++t1]=i;
         while(h2<=t2&&upmx[cnt<<1|1][i]<upmx[cnt<<1|1][q2[t2]])t2--;q2[++t2]=i;
        while(h1<=t1&&h2<=t2&&i-p+1>downmx[cnt<<1][q1[h1]]+upmx[cnt<<1|1][q2[h2]]){
            p++;
            while(h1<=t1&&q1[h1]<p)h1++;while(h2<=t2&&q2[h2]<p)h2++;
        }
        sum[cnt][i]=max(sum[cnt<<1][i],sum[cnt<<1|1][i]);
        if(h1<=t1&&h2<=t2)sum[cnt][i]=max(sum[cnt][i],i-p+1);
    //    cout<<len1<<" "<<len2<<" "<<sum[cnt][i]<<endl; 
     }
     for(int i=l;i<=r;++i){
         upmx[cnt][i]=upmx[cnt<<1][i]+(upmx[cnt<<1][i]==len1?upmx[cnt<<1|1][i]:0);
         downmx[cnt][i]=downmx[cnt<<1|1][i]+(downmx[cnt<<1|1][i]==len2?downmx[cnt<<1][i]:0);
     }
}
void build(int cnt,int l,int r){
    if(l==r){
        for(int i=1;i<=m;++i)
          upmx[cnt][i]=downmx[cnt][i]=sum[cnt][i]=a[l][i];
        return;
    }
    int mid=(l+r)>>1;
    build(cnt<<1,l,mid);build(cnt<<1|1,mid+1,r);
    merge(cnt,1,m,mid-l+1,r-mid);
}
void upd(int cnt,int l,int r,int x,int y){
    if(l==r){
        sum[cnt][y]^=1;upmx[cnt][y]=downmx[cnt][y]=sum[cnt][y];
        return;
    }
    int mid=(l+r)>>1;
    if(mid>=x)upd(cnt<<1,l,mid,x,y);
    else upd(cnt<<1|1,mid+1,r,x,y);
    merge(cnt,1,m,mid-l+1,r-mid); 
}
void merge2(int cnt,int l,int r,int len){
     int h1=1,h2=1,t1=0,t2=0,p=l;
     for(int i=l;i<=r;++i){
         while(h1<=t1&&downmx[0][i]<=downmx[0][q1[t1]])t1--;q1[++t1]=i;
         while(h2<=t2&&upmx[cnt][i]<=upmx[cnt][q2[t2]])t2--;q2[++t2]=i;
        while(h1<=t1&&h2<=t2&&i-p+1>downmx[0][q1[h1]]+upmx[cnt][q2[h2]]){
            p++;
            while(h1<=t1&&q1[h1]<p)h1++;while(h2<=t2&&q2[h2]<p)h2++;
        }
        ans=max(ans,min(i-l+1,sum[cnt][i]));
        if(h1<=t1&&h2<=t2)ans=max(ans,i-p+1);
     }
     for(int i=l;i<=r;++i){
         upmx[0][i]=upmx[0][i]+(upmx[0][i]==now?upmx[cnt][i]:0);
         downmx[0][i]=downmx[cnt][i]+(downmx[cnt][i]==len?downmx[0][i]:0);
     }
}
void query(int cnt,int l,int r,int L,int R,int s,int t){
    if(l>=L&&r<=R){
        merge2(cnt,s,t,r-l+1);
        now+=(r-l+1);
        return;
    }
    int mid=(l+r)>>1;
    if(mid>=L)query(cnt<<1,l,mid,L,R,s,t);
    if(mid<R)query(cnt<<1|1,mid+1,r,L,R,s,t);
}
int main(){
    n=rd();m=rd();int q=rd();
    for(int i=1;i<=n;++i)
        for(int j=1;j<=m;++j)a[i][j]=rd();
    build(1,1,n);
    int opt,x,y,l,s,r,t;
    while(q--){
        opt=rd();
        if(!opt){
            x=rd();y=rd();
            upd(1,1,n,x,y);
        }
        else{
            l=rd();s=rd();r=rd();t=rd();
            ans=0;now=0;
            for(int i=s;i<=t;++i)upmx[0][i]=downmx[0][i]=0;
            query(1,1,n,l,r,s,t);
            printf("%d\n",ans); 
        }
    }
    return 0;
}

posted @ 2019-02-19 10:17 comld 阅读(392) 评论(0) 编辑收藏举报

刷新页面返回顶部

comld

[Code+#3]寻找车位

公告