[HNOI2013]切糕

题目描述

经过千辛万苦小 A 得到了一块切糕，切糕的形状是长方体，小 A 打算拦腰将切糕切成两半分给小 B。出于美观考虑，小 A 希望切面能尽量光滑且和谐。于是她找到你，希望你能帮她找出最好的切割方案。

出于简便考虑，我们将切糕视作一个长 P、宽 Q、高 R 的长方体点阵。我们将位于第 z层中第 x 行、第 y 列上(1≤x≤P, 1≤y≤Q, 1≤z≤R)的点称为(x,y,z)，它有一个非负的不和谐值 v(x,y,z)。一个合法的切面满足以下两个条件：

1. 与每个纵轴(一共有 P*Q 个纵轴)有且仅有一个交点。即切面是一个函数 f(x,y)，对于所有 1≤x≤P, 1≤y≤Q,我们需指定一个切割点 f(x,y),且 1≤f(x,y)≤R。

2. 切面需要满足一定的光滑性要求，即相邻纵轴上的切割点不能相距太远。对于所有的 1≤x,x’≤P 和 1≤y,y’≤Q，若|x-x’|+|y-y’|=1，则|f(x,y)-f(x’,y’)| ≤D，其中 D 是给定的一个非负整数。 可能有许多切面f 满足上面的条件，小A 希望找出总的切割点上的不和谐值最小的那个。

题解

先考虑没有限制的情况，显然可以直接贪心的选出每一列的最小值。

如果转化为网络流的模型，就是每一列从下向上连边。

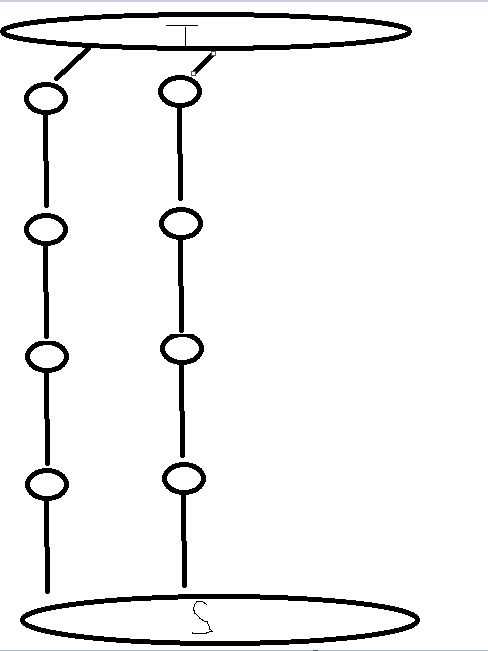
现在有了一些限制，有些情况是不合法的。

相邻两列之间的元素位置不能超过d。

那么我们需要把这种情况叉掉。

做法是每个点向相邻位置的i-d连inf边。

因为每一种不合法的情况否可以看做是一个元素的位置比另一个元素的位置大超过d。

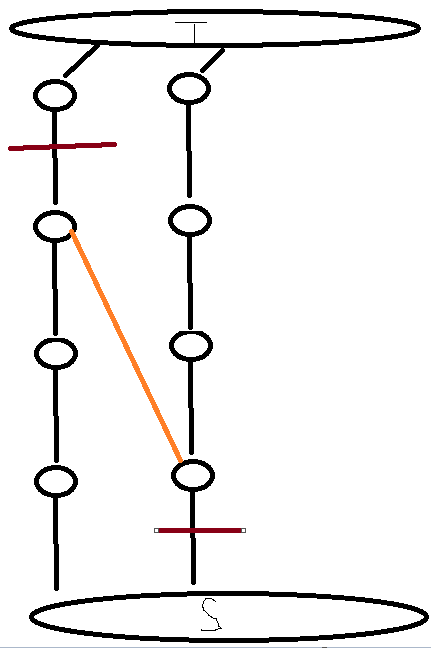
d=2当我们连出这条橙色边之后，如果我们再取那两条棕色边作为割边的话就会不合法，这样就可以把不合法情况判掉了。

代码

#include<iostream>
#include<cstdio>
#include<map>
#include<cstring>
#include<queue>
#define N 200002
#define inf 2e9
using namespace std;
const int dx[4]={0,0,1,-1};
const int dy[4]={1,-1,0,0};
queue<int>q;
int tot=1,head[N],deep[N],cur[N],n,Q,r,p,id[41][41][41],d;
long long ans;
inline int rd(){
    int x=0;char c=getchar();bool f=0;
    while(!isdigit(c)){if(c=='-')f=1;c=getchar();}
    while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return f?-x:x;
}
struct edge{
    int n,to,l;
}e[N*6];
inline void add(int u,int v,int l){
    e[++tot].n=head[u];e[tot].to=v;head[u]=tot;e[tot].l=l;
    e[++tot].n=head[v];e[tot].to=u;head[v]=tot;e[tot].l=0;
}
inline bool bfs(int s,int t){
    memset(deep,0,sizeof(deep));
    memcpy(cur,head,sizeof(head));
    deep[s]=1;q.push(s);
    while(!q.empty()){
        int u=q.front();q.pop();
        for(int i=head[u];i;i=e[i].n){
            int v=e[i].to;
            if(!deep[v]&&e[i].l){
                deep[v]=deep[u]+1;q.push(v);
            }
        }
    }
    return deep[t];
}
int dfs(int u,int t,int l){
    if(u==t||!l)return l;
    int f,flow=0;
    for(int &i=cur[u];i;i=e[i].n){
        int v=e[i].to;
        if(deep[v]==deep[u]+1&&(f=dfs(v,t,min(l,e[i].l)))){
            e[i].l-=f;e[i^1].l+=f;flow+=f;l-=f;
            if(!l)break;
        }
    }
    return flow;
}
int main(){
    p=rd();Q=rd();r=rd();d=rd();
    for(int i=0;i<=r;++i)
      for(int j=1;j<=p;++j)
        for(int k=1;k<=Q;++k){
          id[i][j][k]=++n;
          if(!i)add(0,n,inf);
      }
    for(int i=1;i<=p;++i)for(int j=1;j<=Q;++j)add(id[r][i][j],n+1,inf);
    for(int i=1;i<=r;++i){
        for(int j=1;j<=p;++j)
          for(int k=1;k<=Q;++k){
              add(id[i-1][j][k],id[i][j][k],rd());
              if(i>=d)for(int l=0;l<4;++l){
                int xx=j+dx[l],yy=k+dy[l];
              if(id[i-d][xx][yy])add(id[i][j][k],id[i-d][xx][yy],inf);    
            }
          }
    }
    while(bfs(0,n+1))ans+=dfs(0,n+1,inf);
    cout<<ans;
    return 0;
}