[USACO18DEC]Balance Beam

题目描述

https://www.luogu.org/problemnew/show/P5155

题解

先考虑这么一个问题，我们设f[i]表示从i点出发，按照题意去走，走到n的概率。

初值f[0]=0(到0相当于死了)，f[n]=1(已经到终点了)。

f[i]=(f[i-1]+f[i+1])/2

解得f[x]=x/n。

归纳可证：对于点对a,b和中间任意一个i，i的期望为(f(a)*(b-i)+f(b)*(i-a))/(b-a)

然后我们发现一个神奇的事情：我们求得i点的期望就是ab连线上i出的y值。

 

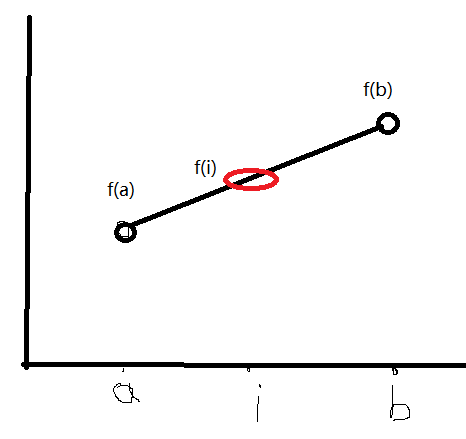
这个算一算就可以出来。

然后这个题期望带上了权值，其实一个道理，我们求最优解，其实只需要对n个点求凸包计算就好了。

细节：卡精度卡到丧心病狂，不能用点斜式，直接用上面的式子算点值就可以了。

代码

#include<iostream>
#include<cstdio>
#define N 100002
using namespace std;
typedef long long ll;
ll n,a[N],top;
inline int rd(){
    int x=0;char c=getchar();bool f=0;
    while(!isdigit(c)){if(c=='-')f=1;c=getchar();}
    while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return f?-x:x;
}
struct point{
    ll x,y;
    point operator -(const point &b)const{return point{x-b.x,y-b.y};};
    double operator *(const point &b)const{return x*b.y-y*b.x;}
}st[N];
int main(){
    n=rd();
    for(int i=1;i<=n;++i)a[i]=rd(),a[i]*=100000;
    st[1]=point{0,0};st[2]=point{1,a[1]};top=2;
    for(int i=2;i<=n+1;++i){
        point x=point{i,a[i]};
        while(top>1&&(st[top]-st[top-1])*(x-st[top-1])>=0)top--;
        st[++top]=x;
    }
    int p=2;
    for(int i=1;i<=n;++i){
        while(st[p].x<i)p++;
        if(st[p].x==i)printf("%lld\n",st[p].y);
        else printf("%lld\n",(st[p].y*(i-st[p-1].x)+st[p-1].y*(st[p].x-i))/(st[p].x-st[p-1].x));
    }
    return 0;
}