Crash 的文明世界

题目描述

给一棵树，求以每个点为根时下列式子的值。

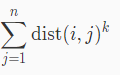
题解

当k=1时这就是一个经典的换根dp问题。

所以这道题还是要用换根dp解决。

部分分做法：

考虑转移时是这样的一个形式(图是抄的)。

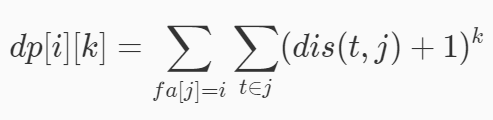
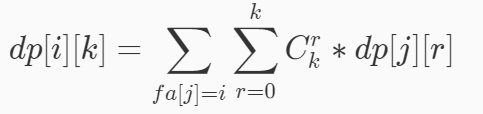
用二项式定理展开就可以nk²做了。

观察到结果是一个x^k的形式。

然后这个可以用斯特林数代换。

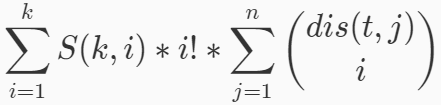
我们可以先求出每个点的后面的东西，在乘上前面的就是答案了。

这是个组合数，可以用组合数的递推解决。

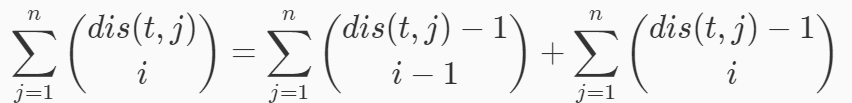
代码

#include<iostream>
#include<cstdio>
#define N 50009
#define KK 151
using namespace std;
typedef long long ll;
const int mod=10007;
int dp[N][KK],f[KK],h[KK],jie[KK];
int n,m,a[N],tot,head[N],K,s[KK][KK];
inline ll rd(){
    ll x=0;char c=getchar();bool f=0;
    while(!isdigit(c)){if(c=='-')f=1;c=getchar();}
    while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return f?-x:x;
}
struct edge{int n,to;}e[N<<1];
inline void add(int u,int v){
    e[++tot].n=head[u];e[tot].to=v;head[u]=tot;
    e[++tot].n=head[v];e[tot].to=u;head[v]=tot;
}
void dfs(int u,int fa){
  dp[u][0]=1;
  for(int i=head[u];i;i=e[i].n)if(e[i].to!=fa){
        int v=e[i].to;dfs(v,u);
        (dp[u][0]+=dp[v][0])%=mod;
        for(int j=1;j<=K;++j)(dp[u][j]+=dp[v][j]+dp[v][j-1])%=mod;
  }
}
void dfs2(int u,int fa){
   for(int i=head[u];i;i=e[i].n)if(e[i].to!=fa){
        int v=e[i].to;
        for(int j=0;j<=K;++j)f[j]=0;
        f[0]=dp[u][0]-dp[v][0];
        for(int j=1;j<=K;++j)(f[j]+=dp[u][j]-dp[v][j-1]-dp[v][j]+mod*2)%=mod;
         (dp[v][0]+=f[0])%=mod;
        for(int j=1;j<=K;++j)(dp[v][j]+=f[j]+f[j-1])%=mod;
        dfs2(v,u);
  }
}
int main(){
   n=rd();K=rd();int u,v;
   for(int i=1;i<n;++i){u=rd();v=rd();add(u,v);}
   s[0][0]=1;
   for(int i=1;i<=K;++i){
         s[i][1]=1;
         for(int j=2;j<=i;++j)
           s[i][j]=(s[i-1][j-1]+s[i-1][j]*j)%mod;
   }
   jie[0]=1;
   for(int i=1;i<=K;++i)jie[i]=jie[i-1]*i%mod;
   dfs(1,0);
   dfs2(1,0);
   for(int i=1;i<=n;++i){
        int ans=0;
     for(int j=0;j<=K;++j)(ans+=s[K][j]*jie[j]%mod*dp[i][j]%mod)%=mod;
     printf("%d\n",ans);
   } 
   return 0;
}