置换群学习笔记

POJ2409

给一个长度为n的环，可以旋转翻转，问本质不同的方案有多少个。

首先有2*n个置换。

然后旋转的情况轨道数是gcd(i,n)，数论上应该有这个东西。

然后翻转的情况分两种，如果是奇数，那么可以C(n,1)固定一个点，然后轨道数(n+1)/2.

如果是偶数，那么如果两点一线，就是n/2+1，如果两边一线就是n/2。

代码

#include<iostream>
#include<cstdio>
using namespace std;
typedef long long ll;
int c,n;
ll ans;
inline int rd(){
    int x=0;char c=getchar();bool f=0;
    while(!isdigit(c)){if(c=='-')f=1;c=getchar();}
    while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return f?-x:x;
}
inline ll power(ll x,int y){
    ll ans=1;
    while(y){
        if(y&1)ans=ans*x;x=x*x;y>>=1;
    }
    return ans;
}
inline int gcd(int x,int y){return y?gcd(y,x%y):x;}
int main(){
    while(scanf("%d%d",&c,&n)!=EOF){
        if(!c||!n)break;
        ans=0;
        for(int i=1;i<=n;++i)ans+=power(c,gcd(i,n));
        if(n&1)ans+=n*power(c,(n+1)/2);
        else ans+=n/2*(power(c,n/2)+power(c,n/2+1));
        ans/=2*n;
        printf("%lld\n",ans);
    }
    return 0;
} 

 POJ2888

题目大意：长度为n的环，有m种颜色，规定k对关系，表示x颜色不能喝y颜色挨着，旋转同构，求方案数。

n<=1e9,m<=10

先考虑没有不合法的，我们可以根号枚举GCD的值，然后算一下pow(c,i)*phi(n/i)，和上一道题一样。

但是现在有了限制，我们就不能直接pow了。

考虑已经枚举了轨道数。

绿色条的长度就是轨道数，蓝色的点构成了一个轨道，那么每一段绿色的部分必须一样。

那么我们只需要求出长度为轨道数的合法序列，而且头尾一样的方案数。

这个用矩阵快速幂就可以了。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
const int mod=9973;
ll n,m,t,k,ans;
inline int rd(){
    int x=0;char c=getchar();bool f=0;
    while(!isdigit(c)){if(c=='-')f=1;c=getchar();}
    while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return f?-x:x;
}
inline ll power(ll x,int y){
    ll ans=1;x%=mod;
    while(y){if(y&1)ans=ans*x%mod;x=x*x%mod;y>>=1;}
    return ans;
}
inline ll get_phi(int x){
    ll ans=x;
    for(int i=2;i*i<=x;++i)if(x%i==0){    
        ans=ans*(i-1)/i;
        while(x%i==0)x/=i;
    }
    if(x!=1)ans=ans*(x-1)/x;//!!!
    return ans;
}
struct matrix{
    ll a[11][11];
    matrix(){memset(a,0,sizeof(a));}
    inline void clear(){memset(a,0,sizeof(a));} 
    matrix operator *(const matrix &b)const{
        matrix c;
        for(int i=1;i<=m;++i)
          for(int j=1;j<=m;++j){
            for(int k=1;k<=m;++k)c.a[i][j]+=a[i][k]*b.a[k][j];c.a[i][j]%=mod;
        }
        return c;
    }
}w;
inline ll C(ll k){
    matrix ans,b=w;ll an=0;
    for(int i=1;i<=m;++i)ans.a[i][i]=1;
    while(k){if(k&1)ans=ans*b;b=b*b;k>>=1;}
    for(int i=1;i<=m;++i)an+=ans.a[i][i];an%=mod;
    return an;
} 
int main(){
    t=rd();int x,y;
    while(t--){
        n=rd();m=rd();k=rd();
        ans=0;w.clear();
        for(int i=1;i<=m;++i)for(int j=1;j<=m;++j)w.a[i][j]=1;
        for(int i=1;i<=k;++i){x=rd();y=rd();w.a[x][y]=w.a[y][x]=0;}
        for(int i=1;i*i<=n;++i)if(n%i==0){//枚举gcd(i,n)的值，也就是轨道数 
            (ans+=C(i)*get_phi(n/i)%mod)%=mod;
            if(i*i!=n){(ans+=C(n/i)*get_phi(i)%mod)%=mod;}
        }    
        ans=ans*power(n,mod-2)%mod;
        printf("%lld\n",ans);
    }
    return 0;
} 

 HDU5868

和上题基本一样，就是只有两种颜色，两个白色不能在一起。

所以有区别的只有求长度为n时的合法序列，注意它其实是环状的。

有递推式dp[n]=dp[n-1]+dp[n-2] dp[0]=2 dp[1]=1.

这个递推式我也不知道怎么推出来的，只好口胡一下(真·瞎说)，每种状态用两个01表示，表示序列的末尾和开头，1是黑0是白。

dp[n-1] 11>>11 10>>>0 01>>11 dp[n-2] 01>>01 10>>10 11>>01

发现三种状态可以合并，口胡完毕。。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
const int mod=1e9+7;
ll t,n,ans;
inline ll power(ll x,int y){
    ll ans=1;
    while(y){if(y&1)ans=ans*x%mod;x=x*x%mod;y>>=1;}
    return ans;
}
inline ll get_phi(ll x){
    ll ans=x;
    for(int i=2;i*i<=x;++i)if(x%i==0){
        ans=ans*(i-1)/i;
        while(x%i==0)x/=i;
    }
    if(x!=1)ans=ans*(x-1)/x;
    return ans;
} 
struct matrix{
    ll a[3][3];
    matrix(){memset(a,0,sizeof(a));}
    matrix operator *(const matrix &b)const{
        matrix c;
        for(int i=1;i<=2;++i)
          for(int j=1;j<=2;++j)
              for(int k=1;k<=2;++k)(c.a[i][j]+=a[i][k]*b.a[k][j]%mod)%=mod;
        return c;
    }
}w;
inline ll calc(ll x){
    if(x==1)return 1;if(x==2)return 3;
    matrix dp,e=w;dp.a[1][1]=1;dp.a[1][2]=3;
    x-=2;
    while(x){if(x&1)dp=dp*e;e=e*e;x>>=1;}
    return dp.a[1][2];
} 
int main(){
    w.a[1][2]=w.a[2][1]=w.a[2][2]=1;
    while(scanf("%lld",&n)!=EOF){
        ans=0;
        if(n==1){puts("2");continue;}
        for(int i=1;i*i<=n;++i)if(n%i==0){
            (ans+=get_phi(n/i)*calc(i)%mod)%=mod;
            if(i*i!=n)(ans+=get_phi(i)*calc(n/i)%mod)%=mod;
        }
        ans=ans*power(n,mod-2)%mod;
        printf("%lld\n",ans);
    }
    return 0;
}

 BZOJ1815有色图

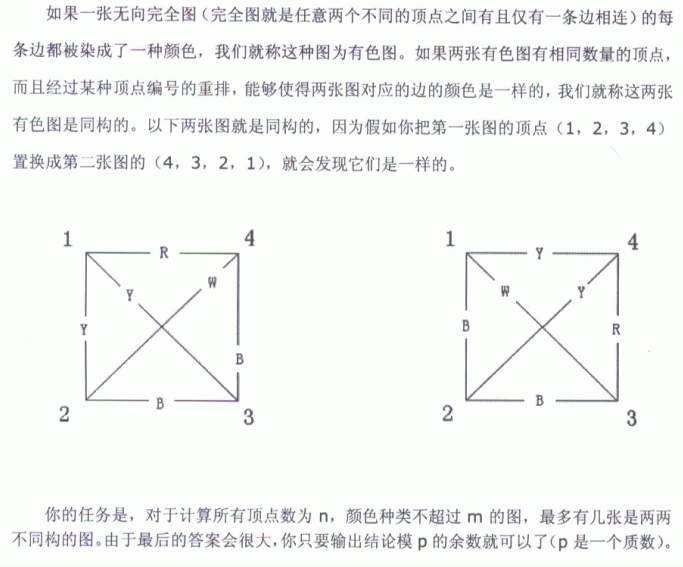
首先这道题一看就是要用polya定理计数的。

假设我们现在有了一些置换{集合1}{集合2}{集合3}。。。

那么我们考虑这种情况下不动点的数目是多少。

考虑在一个置换内的点集，我们可以让它们构成一个环，然后去转它，转n次会回到原来的位置，那么一条边会不停的转，在每次转的过程中会遍历所有长度相同的边，所以这些边的颜色必须一样，所以轨道数为n/2

不在一个置换内的点集，设大小为l1和l2，那么 两个环转lcm(l1,l2)次会转回去，那么环长就是lcm(l1,l2)轨道数为l1*l2/lcm(l1,l2)。

然后算完了不动点，还要算一下不同置换个数。

考虑置换为a1<a2<a3<an

考虑每个点在哪个置换中，可得答案为n!/∑a1!然每一组置换构成一个环，方案为(ai-1)!，然后长得一样的置换的排列方法k!

最后的置换个数为n!/(sigma(ai!)*k!置换个数为n!，dfs算一下。

代码

#include<iostream>
#include<cstdio>
#define N 102
using namespace std;
typedef long long ll; 
ll cnt1,cnt2=1,n,m,p,ans,st[N],top;
inline ll power(ll x,ll y){
    ll ans=1;
    while(y){
        if(y&1)ans=ans*x%p;
        x=x*x%p;
        y>>=1;
    }
    return ans;
}
inline ll ni(ll x){return power(x,p-2);}
int gcd(int x,int y){return y?gcd(y,x%y):x;}
void dfs(int num,int shang,int same){
    if(!num){(ans+=power(m,cnt1)*ni(cnt2)%p)%=p;return;}
    int mem1=cnt1,mem2=cnt2;
    for(int i=1;i<=min(num,shang);++i){
        st[++top]=i;
        cnt1+=(i/2);
        for(int j=1;j<top;++j)cnt1+=gcd(st[j],i);
        cnt2=cnt2*i%p;
        if(st[top]==st[top-1])cnt2=cnt2*(same+1)%p;
        dfs(num-i,i,st[top]==st[top-1]?same+1:1);
        top--;cnt1=mem1;cnt2=mem2;
    } 
} 
int main(){
    scanf("%lld%lld%lld",&n,&m,&p);
    dfs(n,n,1);
    cout<<ans;
    return 0;
}