POJ 3013 Big Christmas Tree

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　Big Christmas Tree

Time Limit: 3000MS		Memory Limit: 131072K
Total Submissions:26471		Accepted: 5745

Description

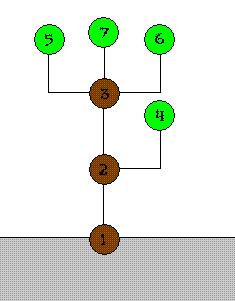Christmas is coming to KCM city. Suby the loyal civilian in KCM city is preparing a big neat Christmas tree. The simple structure of the tree is shown in right picture.

The tree can be represented as a collection of numbered nodes and some edges. The nodes are numbered 1 through n. The root is always numbered 1. Every node in the tree has its weight. The weights can be different from each other. Also the shape of every available edge between two nodes is different, so the unit price of each edge is different. Because of a technical difficulty, price of an edge will be (sum of weights of all descendant nodes) × (unit price of the edge).

Suby wants to minimize the cost of whole tree among all possible choices. Also he wants to use all nodes because he wants a large tree. So he decided to ask you for helping solve this task by find the minimum cost.

Input

The input consists of T test cases. The number of test cases T is given in the first line of the input file. Each test case consists of several lines. Two numbers v, e (0 ≤ v, e ≤ 50000) are given in the first line of each test case. On the next line, v positive integers w_i indicating the weights of v nodes are given in one line. On the following e lines, each line contain three positive integers a, b, cindicating the edge which is able to connect two nodes a and b, and unit price c.

All numbers in input are less than 2¹⁶.

Output

For each test case, output an integer indicating the minimum possible cost for the tree in one line. If there is no way to build a Christmas tree, print “No Answer” in one line.

Sample Input

2
2 1
1 1
1 2 15
7 7
200 10 20 30 40 50 60
1 2 1
2 3 3
2 4 2
3 5 4
3 7 2
3 6 3
1 5 9

Sample Output

15
1210

思路
求出各个点的最短路，分别乘上每个点的权值在累和就行了
注意n==1与n==0的情况，要输出0
这题是我第一次套板子，以前我做题全是手撸，可是我还是差不多wa了一页，我还以为是我套板子的报应。。。。。

代码

#include<iostream>
#include<queue>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn = 50086*4;
const long long inf = 2100000000000000;

int u[maxn],v[maxn];
long long w[maxn];
int first[maxn],Next[maxn];
long long dis[maxn];
long long pri[maxn];
bool book[maxn];
int n,m;
struct node
{
    int num;
    long long dis;

    bool operator<(const node x)const
    {
        return dis>x.dis;
    }
};
int main()
{
    int T;
    scanf("%d",&T);
    while(T--){
        scanf("%d%d",&n,&m);
        memset(pri,0,sizeof(pri));
        for(int i=1;i<=n;i++){
            scanf("%lld",&pri[i]);
        }
        memset(book,0,sizeof(book));
        memset(first,-1,sizeof(first));
        for(int i=1;i<=m;i++){
            scanf("%d%d%lld",&u[i],&v[i],&w[i]);
        }if(n==0||n==1){printf("0\n");continue;}
        for(int i=1;i<=m;i++){
            u[i+m]=v[i];
            v[i+m]=u[i];
            w[i+m]=w[i];
        }
        for(int i=1;i<=n;i++){
            first[i]=-1;
        }

        fill(dis,dis+50086,inf);
        for(int i=1;i<=2*m;i++){
            Next[i]=first[u[i]];
            first[u[i]]=i;
        }
        priority_queue<node>q;
        node exa;
        exa.dis=0;
        exa.num=1;
        dis[1]=0;
        q.push(exa);
        int k;
        while(!q.empty()){
            exa=q.top();q.pop();
            if(book[exa.num]){continue;}
            k=first[exa.num];
            book[exa.num]=true;
            while(k!=-1){
                if(dis[v[k]]>dis[u[k]]+w[k]&&book[v[k]]==false){
                    dis[v[k]]=dis[u[k]]+w[k];
                    exa.dis=dis[v[k]];
                    exa.num=v[k];
                    q.push(exa);
                }
                k=Next[k];
            }
        }
        long long ans=0;
        for(int i=2;i<=n;i++){
            ans+=dis[i]*pri[i];
            if(dis[i]==inf){
                ans=-1;break;
            }
        }
        if(ans==-1||n==0){printf("No Answer\n");}
        else printf("%lld\n",ans);
    }
}