HDU - 5015 233 Matrix (矩阵快速幂）

In our daily life we often use 233 to express our feelings. Actually, we may say 2333, 23333, or 233333 ... in the same meaning. And here is the question: Suppose we have a matrix called 233 matrix. In the first line, it would be 233, 2333, 23333... (it means a _0,1 = 233,a _0,2 = 2333,a _0,3 = 23333...) Besides, in 233 matrix, we got a_i,j = a _i-1,j +a _i,j-1( i,j ≠ 0). Now you have known a _1,0,a _2,0,...,a _n,0, could you tell me a _n,m in the 233 matrix?

InputThere are multiple test cases. Please process till EOF. 

For each case, the first line contains two postive integers n,m(n ≤ 10,m ≤ 10 ⁹). The second line contains n integers, a _1,0,a _2,0,...,a _n,0(0 ≤ a _i,0 < 2 ³¹).OutputFor each case, output a _n,m mod 10000007.Sample Input

1 1
1
2 2
0 0
3 7
23 47 16

Sample Output

234
2799
72937

题意：
a[i][j]=a[i-1][j]+a[i][j-1];
a[0][1]=233,a[0][2]=2333,a[0][3]=23333,......
a[1][0]到a[n][0]由输入给出，求a[n][m];

思路：
本来打算直接用a[i][j]=a[i-1][j]+a[i][j-1]作为公式进行推导，发现并不可行。
实际上是直接对每一列进行操作。
写完这题，大概矩阵快速幂才是真的入门。

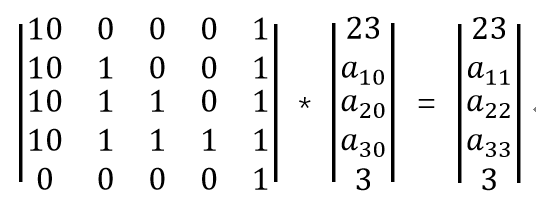
#include<iostream>
#include<algorithm>
#include<vector>
#include<stack>
#include<queue>
#include<map>
#include<set>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<ctime>
#define fuck(x) cout<<#x<<" = "<<x<<endl;
#define debug(a,i) cout<<#a<<"["<<i<<"] = "<<a[i]<<endl;
#define ls (t<<1)
#define rs ((t<<1)+1)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 100086;
const int maxm = 100086;
const int inf = 2.1e9;
const ll Inf = 999999999999999999;
const int mod = 10000007;
const double eps = 1e-6;
const double pi = acos(-1);

ll num[15];


struct Matrix{
    ll mp[15][15];
};
Matrix mul(Matrix a,Matrix b,int n){
    Matrix ans;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            ans.mp[i][j]=0;
            for(int k=1;k<=n;k++){
                ans.mp[i][j]+=a.mp[i][k]*b.mp[k][j];
            }
            ans.mp[i][j]%=mod;
        }
    }
    return ans;
}

Matrix q_pow(Matrix a,int b,int n){
    Matrix ans;
    memset(ans.mp,0,sizeof(ans.mp));
    for(int i=1;i<=n;i++){
        ans.mp[i][i]=1;
    }
    while (b){
        if(b&1){
            ans=mul(ans,a,n);
        }
        b>>=1;
        a=mul(a,a,n);
    }
    return ans;
}


int main()
{
//    ios::sync_with_stdio(false);
//    freopen("in.txt","r",stdin);

    int n,m;
    while(scanf("%d%d",&n,&m)!=EOF){
        for(int i=1;i<=n;i++){
            scanf("%lld",&num[i]);
        }
        Matrix exa;
        memset(exa.mp,0,sizeof(exa.mp));
        int t=0;
        exa.mp[n+2][n+2]=1;
        for(int i=1;i<=n+1;i++){
            exa.mp[i][1]=10;exa.mp[i][n+2]=1;
            for(int j=1;j<=t;j++){
                exa.mp[i][j+1]=1;
            }
            t++;
        }
        exa=q_pow(exa,m,n+2);
        ll ans=0;
        num[0]=23;num[n+1]=3;
        for(int i=1;i<=n+2;i++){
            ans+=exa.mp[n+1][i]*num[i-1];
            ans%=mod;
        }
        printf("%lld\n",ans);


    }

    return 0;
}