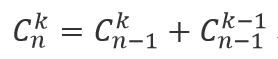HDU - 6333 Problem B. Harvest of Apples （莫队）

There are nn apples on a tree, numbered from 11 to nn. 
Count the number of ways to pick at most mm apples. 

Input

The first line of the input contains an integer TT (1≤T≤105)(1≤T≤105) denoting the number of test cases. 
Each test case consists of one line with two integers n,mn,m (1≤m≤n≤105)(1≤m≤n≤105). 
Output

For each test case, print an integer representing the number of ways modulo 109+7109+7.Sample Input

2
5 2
1000 500

Sample Output

16
924129523

题意：
给定多个n,m，求C(n,m)
思路:
数据范围比较大，不能进行预处理。
我们可以采用莫队算法解决这个查询问题。

当n变大时，按此试展开，再和原式相比较，便可以得出转换公式。
n变小同理。
k的变化直接加减即可。
注意：变化过程中，可能使n>m,这个时候计算C的函数直接返回0就好了。
逆元要预处理，否则会T。

#include<iostream>
#include<algorithm>
#include<vector>
#include<stack>
#include<queue>
#include<map>
#include<set>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<ctime>
#define fuck(x) cout<<#x<<" = "<<x<<endl;
#define debug(a,i) cout<<#a<<"["<<i<<"] = "<<a[i]<<endl;
#define ls (t<<1)
#define rs ((t<<1)+1)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 100086;
const int maxm = 100086;
const int inf = 2.1e9;
const ll Inf = 999999999999999999;
const int mod = 1000000007;
const double eps = 1e-6;
const double pi = acos(-1);

struct node{
    int l,r;
    int id;
}a[maxm];
ll anss[maxm];
int block;

bool cmp(node a,node b){
    return (a.l/block!=b.l/block)?a.l<b.l:a.r<b.r;
}
int vis[1000008];
ll q_pow(ll a,ll b){
    ll ans=1;
    while(b){
        if(b&1){ans*=a;ans%=mod;}
        a*=a;
        a%=mod;
        b>>=1;
    }
    return ans;
}
ll cal[maxn];
ll inv[maxn];
ll C(int n,int m){
    if(n<0||m<0||m>n){return 0;}
    return cal[n]*inv[m]%mod*inv[n-m]%mod;
}

int main()
{

    cal[0]=1;inv[0]=1;
    for(int i=1;i<maxn;i++){
        cal[i]=cal[i-1]*i;
        cal[i]%=mod;
        inv[i]=q_pow(cal[i],mod-2);
        inv[i]%=mod;
    }

    int m;
    scanf("%d",&m);
    int mx=0;
    for(int i=1;i<=m;i++){
        scanf("%d%d",&a[i].l,&a[i].r);
        a[i].id=i;
        mx=max(mx,a[i].l);
    }
    block=sqrt(mx);
    sort(a+1,a+1+m,cmp);

    ll L=1,R=1;
    ll ans=2;
    for(int i=1;i<=m;i++){
        while(L>a[i].l){
            ans+=C(L-1,R);
            ans%=mod;
            ans*=q_pow(2,mod-2);
            ans%=mod;
            L--;
        }
        while(R<a[i].r){
            R++;
            ans+=C(L,R);
            ans%=mod;
        }
        while(L<a[i].l){
            ans*=2;
            ans%=mod;
            ans-=C(L,R);
            ans+=mod+mod;
            ans%=mod;
            L++;
        }
        while(R>a[i].r){
            ans-=C(L,R);
            ans+=mod+mod;
            ans%=mod;
            R--;
        }
        ans%=mod;
        anss[a[i].id]=ans;
    }

    for(int i=1;i<=m;i++){
        printf("%lld\n",anss[i]);
    }
    return 0;
}