Codeforces Gym101502 I.Move Between Numbers-最短路(Dijkstra优先队列版和数组版)
You are given n magical numbers a1, a2, ..., an, such that the length of each of these numbers is 20 digits.
You can move from the ith number to the jth number, if the number of common digits between ai and aj is exactly 17 digits.
The number of common digits between two numbers x and y is computed is follow:
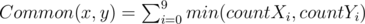 .
.Where countXi is the frequency of the ith digit in the number x, and countYi is the frequency of the ith digit in the number y.
You are given two integers s and e, your task is to find the minimum numbers of moves you need to do, in order to finish at number aestarting from number as.
The first line contains an integer T (1 ≤ T ≤ 250), where T is the number of test cases.
The first line of each test case contains three integers n, s, and e (1 ≤ n ≤ 250) (1 ≤ s, e ≤ n), where n is the number of magical numbers, s is the index of the number to start from it, and e is the index of the number to finish at it.
Then n lines follow, giving the magical numbers. All numbers consisting of digits, and with length of 20 digits. Leading zeros are allowed.
For each test case, print a single line containing the minimum numbers of moves you need to do, in order to finish at number ae starting from number as. If there is no answer, print -1.
1
5 1 5
11111191111191111911
11181111111111818111
11811171817171181111
11111116161111611181
11751717818314111118
3
In the first test case, you can move from a1 to a2, from a2 to a3, and from a3 to a5. So, the minimum number of moves is 3 moves.
这个题的题意没怎么看懂,大体的就是数换位置,如果两个串之间相同的数比较个数(数不一定是连续相同的),把个数小的加起来,正好个数等于17的话,这两个串就建立关系。
然后给你起点和终点,求最少次数(好像),就是迪杰斯特拉跑最短路,然而我写的时候,怎么写都是RE,还是猪队友用他优先队列的板子跑过的.
赛后补题,昨天晚上,一晚上都在杠二维数组存的迪杰斯特拉,还找学长要了学长的板子,都跑不过,一晚上放弃。。今天上午,发现,是初始化没写好,把两份代码的初始化都改好之后都跑过了。。。(MDZZ)
代码1:(队友优先队列版的)
1 //I. Move Between Numbers-和猪一样的过了
2 #include<iostream>
3 #include<cstring>
4 #include<cstdio>
5 #include<algorithm>
6 #include<cmath>
7 #include<queue>
8 #include<vector>
9 using namespace std;
10 const int N=1e3+10;
11 const int inf=0x3f3f3f3f;
12 int a[N][N];
13 char ss[N][N];
14 int n; //n个点1~n m 条边 起点 s
15 int d[N],done[N],p[N]; //d[i]表示i点到起点s的最短路距离
16 //done[u]==1表示u点到起点点s的最短路已经找到
17 //p[i]表示起点s到i的最短路径与i点相连的上一条边
18 struct edge //边结构体
19 {
20 int from,to,dis;
21 };
22 vector<edge> edges; //边集 无向图 边数*2
23 vector<int> g[N]; //g数组存的是边的序号
24 struct mindis //压入优先队列的结构体 因为d[u]和u要绑定起来 才可标记 u是否已确定最短路
25 {
26 int d,u;
27 bool operator <(const mindis& rhs)const{
28 return d>rhs.d; //距离最小值优先 距离相等无所谓 随便一个先出 边权是正的 两个会依次访问 不会影想结果
29 }
30 };
31 void init(int n) //每次输入数据清空容器
32 {
33 for(int i=0;i<=n;i++)
34 g[i].clear();
35 edges.clear();
36 }
37 void addedge(int from,int to,int dis) //加边操作
38 {
39 edges.push_back((edge){from,to,dis}); //将边压入边集
40 int k=edges.size();
41 g[from].push_back(k-1); //k-1为边序号 以后调用边集数组要从下标0开始 所以边的编号从0开始 将边序号压入已from为起点的数组
42 }
43 void dijkstra(int s) //主算法
44 {
45 for(int i=0;i<=n;i++) //把距离初始化为 inf 不能用memset 自己估算一下路径最长有多长 inf定义大一点就好
46 d[i]=inf;
47 d[s]=0; //到自己的最短距离直接设为0
48 priority_queue<mindis> q; //优先队列 小顶堆 最小值优先
49 q.push((mindis){0,s});
50 memset(done,0,sizeof(done)); //初始化数组
51 memset(p,-1,sizeof(p));
52 while(!q.empty()) //队列非空
53 {
54 mindis x=q.top(); //取当前最小值
55 q.pop();
56 int u=x.u;
57 if(done[u]==1) //已确定路径直接跳过
58 continue;
59 done[u]=1; //标记 已确定
60 for(int i=0;i<g[u].size();i++)
61 {
62 edge e =edges[g[u][i]]; //g[u][i]表示以u为起点的第i条边在边集edges中的下标
63 if(d[e.to]>d[u]+e.dis) //满足条件更新距离
64 {
65 d[e.to]=d[u]+e.dis;
66 p[e.to]=g[u][i]; //保存路径
67 q.push((mindis){d[e.to],e.to}); //把更新完的值压入队列
68 }
69 }
70 }
71 }
72 int main(){
73 int t,s,e;
74 scanf("%d",&t);
75 while(t--){
76 scanf("%d%d%d",&n,&s,&e);
77 memset(a,0,sizeof(a));
78 for(int i=1;i<=n;i++){
79 cin>>ss[i];
80 for(int j=0;j<20;j++){
81 int temp=ss[i][j]-'0';
82 a[i][temp]++;
83 }
84 }
85 init(n);
86 for(int i=1;i<=n;i++){
87 for(int j=i+1;j<=n;j++){
88 int ret=0;
89 for(int h=0;h<10;h++)
90 ret+=min(a[i][h],a[j][h]);
91 if(ret==17) {
92 int w=1;
93 addedge(i,j,w);
94 addedge(j,i,w);
95 }
96 }
97 }
98 dijkstra(s);
99 if(d[e]==inf)printf("-1\n");
100 else printf("%d\n",d[e]);
101 }
102 return 0;
103 }
代码2:(自己的板子(垃圾板子。。。),二维数组版的)
1 #include<iostream>
2 #include<cstring>
3 #include<cstdio>
4 #include<algorithm>
5 #include<cmath>
6 using namespace std;
7 #include<bits/stdc++.h>
8 using namespace std;
9 const int N=1e3+10;
10 const int INF=0x3f3f3f3f;
11 char ss[N][N];
12 int q[N][N];
13 int a[N][N]; //存数据的边
14 int dist[N]; //记录最短路的距离
15 int vis[N]; //标记是否访问过
16 int n,s,e;
17 void Dijkstra(){ //迪杰斯特拉算法
18 int tmp,v;
19 memset(vis,0,sizeof(vis));
20 for(int i=1;i<=n;i++)
21 dist[i]=a[s][i]; //首先将dist初始化,将起点与其他点的距离先存进去
22 dist[s]=0; //起点到起点距离为0
23 vis[s]=1; //标记起点被访问过
24 for(int i=1;i<=n-1;i++){ //这里修改了
25 tmp=INF;
26 for(int j=1;j<=n;j++){ //下面的也修改了
27 if(vis[j]==0&&tmp>dist[j]){ //未访问过并且找出与当前要查找的点的最短路径(因为与某个点相连的其他点有多个,找出距离最短的,所以for循环一遍)
28 tmp=dist[j];
29 v=j; //用v存一下当前的最短路径的点
30 }
31 }
32 vis[v]=1;//将当前找到的点标记访问过
33 for(int l=1;l<=n;l++){
34 if(!vis[l]) //找出与之相连的点的最短路径
35 dist[l]=min(dist[l],dist[v]+a[v][l]);//更新d
36 }
37 }
38 }
39 int main(){
40 int t;
41 scanf("%d",&t);
42 while(t--){
43 scanf("%d%d%d",&n,&s,&e);
44 for(int i=1;i<=n;i++){
45 for(int j=1;j<=n;j++){
46 if(i==j)a[i][j]=0; //这里修改了
47 else a[i][j]=INF;
48 }
49 }
50 memset(q,0,sizeof(q));
51 for(int i=1;i<=n;i++){
52 cin>>ss[i];
53 for(int j=0;j<20;j++){
54 int temp=ss[i][j]-'0';
55 q[i][temp]++;
56 }
57 }
58 for(int i=1;i<=n;i++){
59 for(int j=i+1;j<=n;j++){
60 int ret=0;
61 for(int h=0;h<10;h++)
62 ret+=min(q[i][h],q[j][h]);
63 if(ret==17) a[i][j]=a[j][i]=1;
64 }
65 }
66 Dijkstra();
67 if(dist[e]==INF)printf("-1\n");
68 else printf("%d\n",dist[e]);
69 }
70 return 0;
71 }
代码3:(学长的板子,初始化一开始也有问题。。。)
1 //I-头铁,再来一次-学长的板子,加油啊,大兄弟-死了,头被打爆,还是RE2,过了,初始化的时候错了。。。
2 #include<iostream>
3 #include<cstring>
4 #include<cstdio>
5 #include<cmath>
6 #include<algorithm>
7 #include<queue>
8 using namespace std;
9 #define MAX 1005
10 const int INF=0x3f3f3f3f;
11 int arc[1005][1005];
12 int d[1005],n,s,e;
13 char ss[MAX][MAX];
14 int q[MAX][MAX];
15 void dijkstra(int s) // 求s 到其他各点的最短路径
16 {
17 int v,w,k,m;
18 int fina[MAX];
19 int p[MAX];
20 memset(fina,0,sizeof(fina));
21 for(v=1;v<=n; v++) //v=1;数组从1开始
22 {
23 d[v] = arc[s][v];
24 }
25 d[s] = 0;
26 fina[s] = 1;
27 for(v=1; v<n; v++)
28 {
29 m = INF;
30 for(w=1; w<=n; w++)
31 {
32 if( fina[w]==0 && d[w]<m )
33 {
34 k = w;
35 m = d[w];
36 }
37 }
38 fina[k] = 1;
39 for(w=1; w<=n; w++)
40 {
41 if( !fina[w]&& (m+arc[k][w] < d[w] ) )
42 {
43 d[w] = m + arc[k][w];
44 p[w] = k;
45 }
46 }
47 }
48 }
49 int main(){
50 int t;
51 scanf("%d",&t);
52 while(t--){
53 scanf("%d%d%d",&n,&s,&e);
54 for(int i=1;i<=n;i++){
55 for(int j=1;j<=n;j++){
56 if(i==j)arc[i][j]=0;
57 else arc[i][j]=INF;
58 }
59 }
60 memset(q,0,sizeof(q));
61 for(int i=1;i<=n;i++){
62 cin>>ss[i];
63 for(int j=0;j<20;j++){
64 int temp=ss[i][j]-'0';
65 q[i][temp]++;
66 }
67 }
68 for(int i=1;i<=n;i++){
69 for(int j=i+1;j<=n;j++){
70 int ret=0;
71 for(int h=0;h<10;h++)
72 ret+=min(q[i][h],q[j][h]);
73 if(ret==17) arc[i][j]=arc[j][i]=1;
74 }
75 }
76 memset(d,0,sizeof(d));
77 dijkstra(s);
78 if(d[e]==INF)printf("-1\n");
79 else printf("%d\n",d[e]);
80 }
81 return 0;
82 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号