Codeforces Gym101502 F.Building Numbers-前缀和

 

F. Building Numbers

 

time limit per test

3.0 s

memory limit per test

256 MB

input

standard input

output

standard output

In this problem, you can build a new number starting from 1, by performing the following operations as much as you need:

• Add 1 to the current number.
• Add the current number to itself (i.e. multiply it by 2).

For example, you can build number 8 starting from 1 with three operations 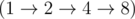. Also, you can build number 10 starting from 1 with five operations .

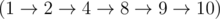You are given an array a consisting of n integers, and q queries. Each query consisting of two integers l and r, such that the answer of each query is the total number of operations you need to preform to build all the numbers in the range from l to r (inclusive) from array a, such that each number ai (l ≤ i ≤ r) will be built with the minimum number of operations.

Input

The first line contains an integer T (1 ≤ T ≤ 50), where T is the number of test cases.

The first line of each test case contains two integers n and q (1 ≤ n, q ≤ 105), where n is the size of the given array, and q is the number of queries.

The second line of each test case contains n integers a1, a2, ..., an (1 ≤ ai ≤ 1018), giving the array a.

Then q lines follow, each line contains two integers l and r (1 ≤ l ≤ r ≤ n), giving the queries.

Output

For each query, print a single line containing its answer.

Example

input

1
5 3
4 7 11 8 10
4 5
1 5
3 3

output

7
18
5

Note

As input/output can reach huge size it is recommended to use fast input/output methods: for example, prefer to use scanf/printfinstead of cin/cout in C++, prefer to use BufferedReader/PrintWriter instead of Scanner/System.out in Java.

In the first query, you need 3 operations to build number 8, and 4 operations to build number 10. So, the total number of operations is 7.

 

这个题要用前缀和处理一下，要不然会超时，数组开的时候注意一下，开小了，RE，很不幸，一开始没用前缀和，数组也开小了，都被卡了，(抱头痛哭)

 

代码:

 1 //F. Building Numbers-前缀和处理，否则超时,数组开小了被卡了一手
 2 #include<iostream>
 3 #include<cstring>
 4 #include<cstdio>
 5 #include<algorithm>
 6 #include<cmath>
 7 using namespace std;
 8 typedef long long ll;
 9 const int N=1e5+10;
10 ll ans[N];
11 ll solve(ll x){
12     int num=0;
13     while(x!=1){
14         if(x%2==0)x/=2;
15         else x--;
16         num++;
17     }
18     return num;
19 }
20 int main(){
21     int t;
22     scanf("%d",&t);
23     while(t--){
24         memset(ans,0,sizeof(ans));
25         int n,m,l,r;
26         scanf("%d%d",&n,&m);
27         ll x;
28         for(int i=1;i<=n;i++){
29             scanf("%lld",&x);
30             ans[i]=ans[i-1]+solve(x);
31         }
32         for(int i=1;i<=m;i++){
33             scanf("%d%d",&l,&r);
34             printf("%lld\n",ans[r]-ans[l-1]);
35         }
36     }
37     return 0;
38 }