牛客网 暑期ACM多校训练营（第一场）A.Monotonic Matrix-矩阵转化为格子路径的非降路径计数，Lindström-Gessel-Viennot引理-组合数学

 

牛客网暑期ACM多校训练营（第一场）

 

 

 

 

 

 

A.Monotonic Matrix

 

 

这个题就是给你一个n*m的矩阵，往里面填{0,1,2}这三种数，要求是A_i,j⩽A_i+1,j，A_i,j⩽A_i,j+1 ，问你一共有几种填法。

变形一下就会发现其实是走非交叉格子路径计数，限制条件下的非降路径问题。就是从左上到右下走格子路径。从上到下为0——n，从左到右为0——m。

考虑 01 和 12 的分界线，是 (n, 0) 到 (0, m) 的两条不相交（可重合）路径，因为起点重合了，所以把其中一条路径往左上平移了一格，平移其中一条变成 (n-1, -1) 到 (-1, m-1) 变成起点 (n, 0) 和 (n-1, -1)，终点 (0, m) 和 (-1, m-1) 的严格不相交路径。可以想一下，分界线将格子图分成三部分，从左上到右下依次为0,1,2。(不好意思，史诗灾难级灵魂脱壳画手。。。)

 

 

叉姐说套Lindström–Gessel–Viennot引理:

 

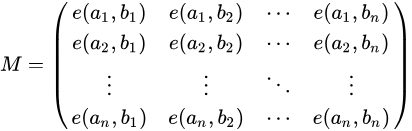
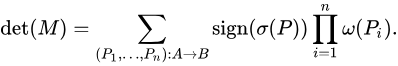
就可以得到公式: (C_{n+m, n}) ² - C_{n+m, m - 1} *C_{n+m, n-1}。

通过组合数求解的模板，就可以了。

关于Lindström–Gessel–Viennot引理，具体的不清楚，有兴趣的自己去看吧。

和本题有关的传送门:

1.格子图中具有一定限制条件的非降路径数

2.非降路径问题 

3.392-非降路径问题

4.Lindström–Gessel–Viennot lemma 应用两则

5.Lindström–Gessel–Viennot lemma

 

 

两份代码：一份自己的垃圾代码，一份叉姐的官方题解标程

代码:(我的)

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long ll;
const int N=1e5+5;
const ll MOD = 1e9+7;
ll F[N], Finv[N], inv[N];
void init()
{
    inv[1] = 1;
    for(ll i = 2; i < N; i ++)
    {
        inv[i] = (MOD - MOD / i) * 1ll * inv[MOD % i] % MOD;
    }
    F[0] = Finv[0] = 1;
    for(ll i = 1; i < N; i ++)
    {
        F[i] = F[i-1] * 1ll * i % MOD;
        Finv[i] = Finv[i-1] * 1ll * inv[i] % MOD;
    }
}
ll comb(ll n, ll m)//c(n,m);
{
    if(m < 0 || m > n) return 0;
    return F[n] * 1ll * Finv[n - m] % MOD * Finv[m] % MOD;
}
int main()
{
    init();
    int n,m;
    while(~scanf("%d%d",&n,&m)){
        ll cnt1=comb(n+m,n)*comb(n+m,n);
        ll cnt2=comb(n+m,m-1)*comb(n+m,n-1);
        ll ans=((cnt1-cnt2)%MOD+MOD)%MOD;
        cout<<ans<<endl;
    }
}

 

代码:(叉姐的官方标程)

#include <bits/stdc++.h>

const int MOD = 1e9 + 7;

const int N = 1005;

int dp[N][N];

void update(int& x, int a)
{
    x += a;
    if (x >= MOD) {
        x -= MOD;
    }
}

int sqr(int x)
{
    return 1LL * x * x % MOD;
}

int main()
{
    dp[0][0] = 1;
    for (int i = 0; i < N; ++ i) {
        for (int j = 0; j < N; ++ j) {
            if (i) {
                update(dp[i][j], dp[i - 1][j]);
            }
            if (j) {
                update(dp[i][j], dp[i][j - 1]);
            }
        }
    }
    int n, m;
    while (scanf("%d%d", &n, &m) == 2) {
        printf("%d\n", static_cast<int>((sqr(dp[n][m]) + MOD - 1LL * dp[n - 1][m + 1] * dp[n + 1][m - 1] % MOD) % MOD));
    }
}

 

 

 

溜了溜了。