计蒜客 18487.Divisions-大数的所有因子个数-Miller_Rabin+Pollard_rho-超快的(大数质因解+因子个数求解公式) (German Collegiate Programming Contest 2015 ACM-ICPC Asia Training League 暑假第一阶段第三场 F)
这一场两个和大数有关的题目,都用到了米勒拉宾算法,有点东西,备忘一下。
F. Divisions
这个题是求一个数的所有因子个数,但是数据比较大,1e18,所以是大数的题目,正常的求因数的或者求质因数的都过不了,因为这一场的K是米勒拉宾判大素数,先过的K题,所以这个题直接头铁用Miller_Rabin+Pollard_rho这两个东西+因子个数求解公式写过去了。
这两个算法的具体原理不清楚。从别人那里知道了一点。
Miller_Rabin算法的作用是判断一个数是否是个素数,算法速度很快,虽然是概率算法,有一定误判概率,不过可以多次运算大幅度减少误判,误判概率与运算次数t有关,为2^(-t);当t够大时,误判的可能性就很小了。
Pollard_rho算法的作用是求一个数的因子,这个复杂度为O(sqrt(p)),p为这个数的因子。
参考来自别的的博客,传送门:算法集锦(特殊模板集)
因为Miller_Rabin+Pollard_rho这两个东西求出来的是一个数的所有质因数,所以最后要用因数个数求解公式来算出来结果。
关于因数个数求解公式:
对于任何一个自然数N,都可以分解质因子得到如下形式:
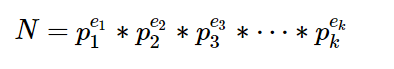
那么,N的因子的个数为:
![]()
如N=100,分解质因子变形为:100=22∗52,N的因子的个数为:f(N)=f(100)=(1+2)∗(1+2)=9。
即:1,2,4,5,10,20,25,50,100。
特判一下1就可以,找出来素因子之后,我是用map记了一下数然后用因子个数求解公式得到的结果。其他的没什么了。
代码:
1 #include<iostream> 2 #include<algorithm> 3 #include<cstring> 4 #include<iomanip> 5 #include<stdio.h> 6 #include<stdlib.h> 7 #include<math.h> 8 #include<cstdlib> 9 #include<set> 10 #include<map> 11 #include<ctime> 12 #include<stack> 13 #include<queue> 14 #include<vector> 15 #include<set> 16 using namespace std; 17 typedef long long ll; 18 const ll NUM=10;//运算次数,Miller_Rabin算法为概率运算,误判率为2^(-NUM); 19 ll t,f[100]; 20 ll mul_mod(ll a,ll b,ll n)//求a*b%n,由于a和b太大,需要用进位乘法 21 { 22 a=a%n; 23 b=b%n; 24 ll s=0; 25 while(b) 26 { 27 if(b&1) 28 s=(s+a)%n; 29 a=(a<<1)%n; 30 b=b>>1; 31 } 32 return s; 33 } 34 ll pow_mod(ll a,ll b,ll n)//求a^b%n 35 { 36 a=a%n; 37 ll s=1; 38 while(b) 39 { 40 if(b&1) 41 s=mul_mod(s,a,n); 42 a=mul_mod(a,a,n); 43 b=b>>1; 44 } 45 return s; 46 } 47 bool check(ll a,ll n,ll r,ll s) 48 { 49 ll ans=pow_mod(a,r,n); 50 ll p=ans; 51 for(ll i=1;i<=s;i++) 52 { 53 ans=mul_mod(ans,ans,n); 54 if(ans==1&&p!=1&&p!=n-1) 55 return true; 56 p=ans; 57 } 58 if(ans!=1) return true; 59 return false; 60 } 61 bool Miller_Rabin(ll n)//Miller_Rabin算法,判断n是否为素数 62 { 63 if(n<2) return false; 64 if(n==2) return true; 65 if(!(n&1)) return false; 66 ll r=n-1,s=0; 67 while(!(r&1)){r=r>>1;s++;} 68 for(ll i=0;i<NUM;i++) 69 { 70 ll a=rand()%(n-1)+1; 71 if(check(a,n,r,s)) 72 return false; 73 } 74 return true; 75 } 76 ll gcd(ll a,ll b) 77 { 78 return b==0?a:gcd(b,a%b); 79 } 80 ll Pollard_rho(ll n,ll c)//Pollard_rho算法,找出n的因子 81 { 82 ll i=1,j,k=2,d,p; 83 ll x=rand()%n; 84 ll y=x; 85 while(true) 86 { 87 i++; 88 x=(mul_mod(x,x,n)+c)%n; 89 if(y==x) return n; 90 if(y>x) p=y-x; 91 else p=x-y; 92 d=gcd(p,n); 93 if(d!=1&&d!=n) return d; 94 if(i==k) 95 { 96 y=x; 97 k+=k; 98 } 99 } 100 } 101 void find(ll n)//找出n的所有因子 102 { 103 if(Miller_Rabin(n)) 104 { 105 f[t++]=n;//保存所有因子 106 return; 107 } 108 ll p=n; 109 while(p>=n)p=Pollard_rho(p,rand()%(n-1)+1);//由于p必定为合数,所以通过多次求解必定能求得答案 110 find(p); 111 find(n/p); 112 } 113 int main() 114 { 115 srand(time(NULL));//随机数设定种子 116 ll n;cin>>n; 117 if(n==1){cout<<"1"<<endl;return 0;} 118 t=0; 119 find(n); 120 sort(f,f+t); 121 map<ll,int>q; 122 for(int i=0;i<t;i++) 123 { 124 q[f[i]]++; 125 } 126 map<ll,int>::iterator it; 127 ll ans=1; 128 for(it=q.begin();it!=q.end();it++) 129 { 130 int s=it->second; 131 ans*=1+s; 132 } 133 cout<<ans<<endl; 134 return 0; 135 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号