Codeforces 946 D.Timetable-数据处理+动态规划(分组背包) 处理炸裂

花了两个晚上来搞这道题。

第一个晚上想思路和写代码，第二个晚上调试。

然而还是菜，一直调不对，我的队友是Debug小能手呀(真的是无敌，哈哈，两个人一会就改好了)

 

D. Timetable

 

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Ivan is a student at Berland State University (BSU). There are n days in Berland week, and each of these days Ivan might have some classes at the university.

There are m working hours during each Berland day, and each lesson at the university lasts exactly one hour. If at some day Ivan's first lesson is during i-th hour, and last lesson is during j-th hour, then he spends j - i + 1 hours in the university during this day. If there are no lessons during some day, then Ivan stays at home and therefore spends 0 hours in the university.

Ivan doesn't like to spend a lot of time in the university, so he has decided to skip some lessons. He cannot skip more than k lessons during the week. After deciding which lessons he should skip and which he should attend, every day Ivan will enter the university right before the start of the first lesson he does not skip, and leave it after the end of the last lesson he decides to attend. If Ivan skips all lessons during some day, he doesn't go to the university that day at all.

Given n, m, k and Ivan's timetable, can you determine the minimum number of hours he has to spend in the university during one week, if he cannot skip more than k lessons?

Input

The first line contains three integers n, m and k (1 ≤ n, m ≤ 500, 0 ≤ k ≤ 500) — the number of days in the Berland week, the number of working hours during each day, and the number of lessons Ivan can skip, respectively.

Then n lines follow, i-th line containing a binary string of m characters. If j-th character in i-th line is 1, then Ivan has a lesson on i-th day during j-th hour (if it is 0, there is no such lesson).

Output

Print the minimum number of hours Ivan has to spend in the university during the week if he skips not more than k lessons.

Examples

input

Copy

2 5 1
01001
10110

output

5

input

Copy

2 5 0
01001
10110

output

8

Note

In the first example Ivan can skip any of two lessons during the first day, so he spends 1 hour during the first day and 4 hours during the second day.

In the second example Ivan can't skip any lessons, so he spends 4 hours every day.

 

 

这个题的意思就是逃课。怎样逃课才能使得最后上完课的时间减去最开始的上课的时间最短。

这里是按0和1来代表有没有课，1代表有课，可以逃。但是最多只能逃k节课。否则就直接坐飞机了。。。

样例01001如果一节也不逃的话，就是最后一个1的位置减去第一个1的位置的距离。为4。

想思路真的是炸裂。

因为是找最优子结构，所以肯定是用动态规划写，有人说是背包，就发现是分组背包。

然后就想怎么处理数据才能用上分组背包。

因为是和1的 位置有关，所以先记录每一组的1的位置。然后num数组计数多少个1。

然后，就是，怎么处理记录位置的数组才能得到距离呢。如果直接贪心的话肯定是不对的，如果是01001010010010，贪心的话，就不对了。所以要考虑一下。

怎么处理呢，举例10110100010，一开始的位置是0，假设数组a存位置就是a[1]=0,a[2]=2,a[3]=3,a[4]=5,a[5]=9。

然后进行删0个1，删1个1，删2个1，删3个1，删。。。一直删num个1。怎么删呢。然后就模拟所有情况。这样做的意思就是假设只处理这一个串。后面会说为什么这样做。

(写的太乱了，凑活看。。。)

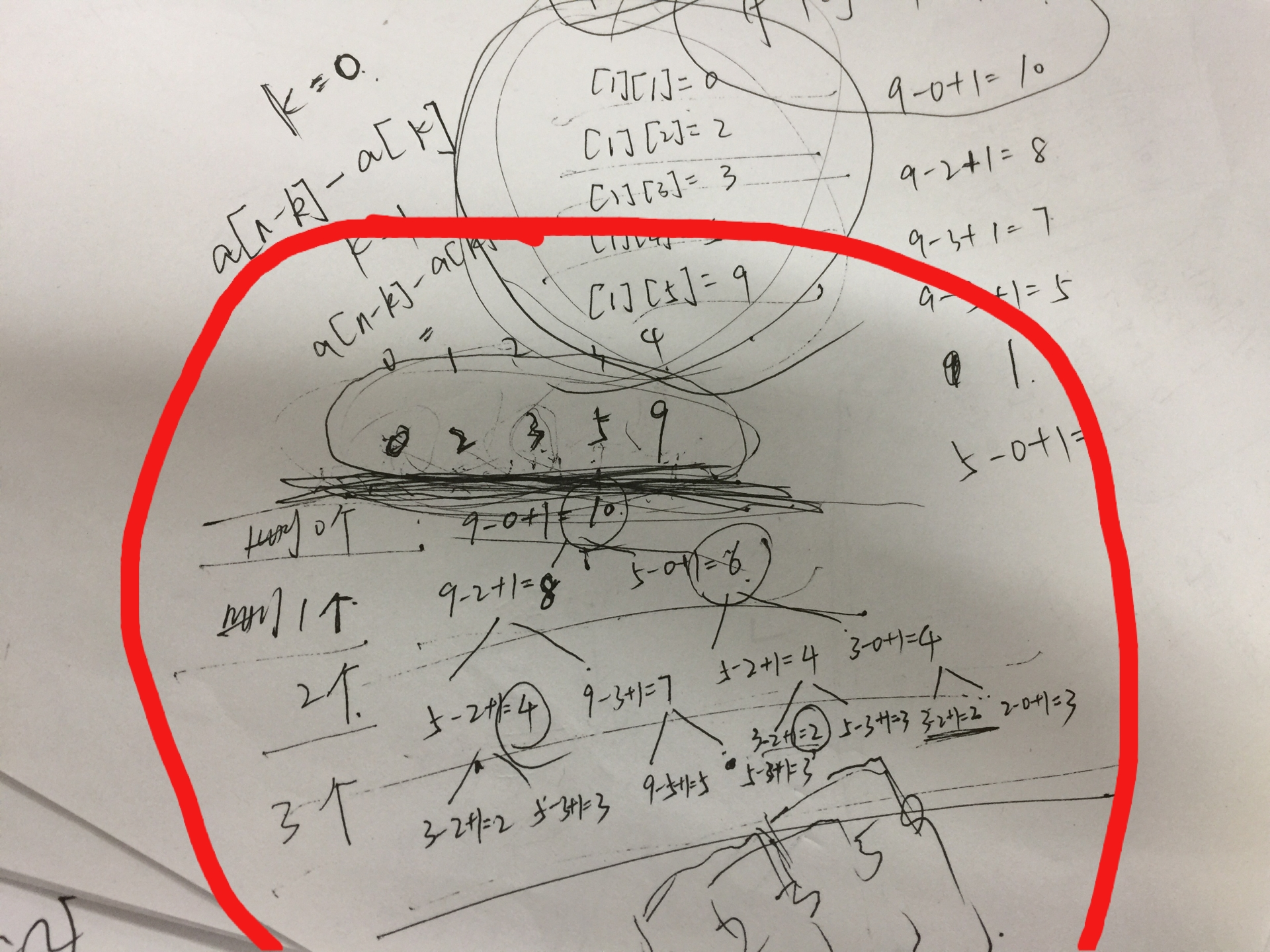发现有重复的情况，才突然想起来(mdzz)，肯定是从两边删才是最完美的呀。就不会有重复了。

但是怎么才能避免呢。贪心肯定不对，然后就想到一种遍历，怎么遍历呢。距离肯定是最后的记录位置的数减去最开始的记录位置的数。我想的就是一个for控制组数，一个for控制删几个数，一个for控制进行操作的两个数的位置，什么意思呢。因为知道有几个数(num数组存的)，所以删j个数的话，就是从两边一共删j个数。还是用上面的例子。

a[1]=0,a[2]=2,a[3]=3,a[4]=5,a[5]=9。

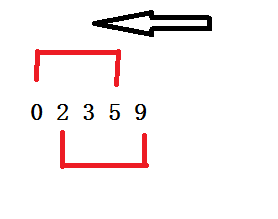这个是什么意思呢。就是删1个1的操作，就是控制位置。我写的是从最后往前推。一直推到头就可以了。然后for循环一边推，一边用数组保存最小值就可以。

但是写的时候智障，只考虑了一直都还有1的情况，没考虑所有1都删掉的情况。还是上面的例子，有5个1，如果5个1都删掉，距离就是0，不是1，这里判断一下。

然后就是写for的时候比较一下这组串中1的个数和要删掉的1的个数哪个小就用哪个作为删j个1的边界值。为什么呢。假设串里就2个1，题目要求删5个1，完全没必要一直删5个1，删2个1就没了，所以比较一下，如果1个个数本来就比要求的删的个数小的话，那肯定是把串里所有的1都删了，所以最后距离是0，这里判断一下就可以。

通过以上的炸裂操作，就可以得到每组串里删j个1的最优值。

自我吐槽:脑子不好，控制位置那里想了好久，最后发现，因为我存位置是从第一个1出现位置开始存的，所以存位置的数组最开始是从1开始的，不是从0开始的。

for(int i=0;i<n;i++){  //控制组数
        int x=min(k,num[i]); //该组中1的个数和要处理的k个1比较一下，取最小值
        for(int j=0;j<=x;j++){ //控制删几个1
            for(int k=0;k<=j;k++){ //控制位置
                if(j==num[i]) //1全删完的判断
                    p[i][j]=0;
                else
                    p[i][j]=min(p[i][j],a[i][num[i]-k]-a[i][1+j-k]+1); //存最短的距离
            }
        }
    }

就是上面这个傻子操作。。。

 

然后就是怎么用分组背包来得到结果呢。

一篇简短介绍分组背包的博客，传送门:我不想当咸鱼

那么背包的最大能装的质量就是题目要求删的1的个数，就是k。最大质量为k。

然后每组的每个物品的质量就是删几个1，如果是删0个1的，那么质量为0，删1个1的，质量就是2，直接就是p[i][j]的j值。

物品的价值就是距离。因为我写的分组背包是用max求最大值的，所以就要找最大节省的时间(就是存位置的一开始的值减去最短距离就是最大节省时间)

然后就可以进行分组背包的操作了。求出来最大节省的时间，然后总的不逃课的时间-最大节省的时间，就是最少的上课时间。游戏结束。

 

代码:

//D-数据处理+分组背包(处理炸裂)
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstdlib>
using namespace std;
typedef long long ll;
const int maxn=500+10;
const int inf=250000+10;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
int h[maxn][maxn],a[maxn][maxn];
int p[maxn][maxn],num[maxn],dp[maxn];
char s[maxn][maxn];
int main(){
    int n,m,k;
    ios;
    cin>>n>>m>>k;
    for(int i=0;i<n;i++)
        cin>>s[i];
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++)
            h[i][j]=s[i][j]-'0'; //h数组存串
    }
    memset(num,0,sizeof(num));
    for(int i=0;i<n;i++){     //记录位置
        for(int j=0;j<m;j++){
            if(h[i][j]==1){
                num[i]++;     //记录1的个数
                a[i][num[i]]=j;  //记录第几个1的位置
            }
        }
    }
    for(int i=0;i<n;i++){     //初始化
        for(int j=0;j<=min(k,num[i]);j++)
            p[i][j]=inf;     
    }
    for(int i=0;i<n;i++){      //i控制组数                           处理距离
        int x=min(k,num[i]);   //找最小的删1的个数
        for(int j=0;j<=x;j++){ //控制删1的操作
            for(int k=0;k<=j;k++){  //控制位置
                if(j==num[i])   //特判一下
                    p[i][j]=0;
                else
                    p[i][j]=min(p[i][j],a[i][num[i]-k]-a[i][1+j-k]+1);  //还有1存在的正常情况
            }
        }
    }
    ll sum=0;
    for(int i=0;i<n;i++)
        sum+=p[i][0];      //将一开始一个1都不删的距离求和
    memset(dp,0,sizeof(dp));
    for(int i=0;i<n;i++)   //i控制组数                                        分组背包
    for(int j=k;j>=0;j--)  //j控制质量
    for(int h=0;h<=min(k,num[i]);h++) //h控制每组的物品数，h也是物品的质量，想一下就懂了
        if(j>=h)     //一开始没写，数组可能会越界，写上就对了。。。
        dp[j]=max(dp[j-h]+(p[i][0]-p[i][h]),dp[j]);    
//    for(int i=0;i<n;i++)
//    {
//        for(int j=0;j<=k;j++)
//        {
//            cout<<p[i][j]<<" ";
//        }
//        cout<<endl;
//    }
//    for(int i=0;i<=k;i++)
//    {
//        cout<<dp[i]<<endl;
//    }
//    cout<<sum<<endl;
    cout<<sum-dp[k]<<endl; //游戏结束
}
//2 7 2
//0100101
//1001101

 

 

 

 

就这样，这题就是处理数据不好想。。。

就这样吧。溜了。。。