HDU 4920.Matrix multiplication-矩阵乘法
Matrix multiplication
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 5236 Accepted Submission(s): 2009
bobo hates big integers. So you are only asked to find the result modulo 3.
The first line contains n (1≤n≤800). Each of the following n lines contain n integers -- the description of the matrix A. The j-th integer in the i-th line equals Aij. The next n lines describe the matrix B in similar format (0≤Aij,Bij≤109).
Print n lines. Each of them contain n integers -- the matrix A×B in similar format.
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<cstdlib> 6 #include<string.h> 7 #include<set> 8 #include<vector> 9 #include<queue> 10 #include<stack> 11 #include<map> 12 #include<cmath> 13 using namespace std; 14 15 int a[805][805],b[805][805],c[805][805]; 16 17 int main(){ 18 int n; 19 while(~scanf("%d",&n)){ 20 for(int i=0;i<n;i++) 21 for(int j=0;j<n;j++){ 22 scanf("%d",&a[i][j]); 23 a[i][j]%=3; 24 c[i][j]=0; 25 } 26 for(int i=0;i<n;i++) 27 for(int j=0;j<n;j++){ 28 scanf("%d",&b[i][j]); 29 b[i][j]%=3; 30 } 31 for(int i=0;i<n;i++) 32 for(int j=0;j<n;j++){ 33 if(!a[i][j])continue;//判断优化 34 for(int k=0;k<n;k++) 35 c[i][k]=c[i][k]+a[i][j]*b[j][k]; 36 } 37 for(int i=0;i<n;i++){ 38 for(int j=0;j<n;j++) 39 if(j==n-1)printf("%d\n",c[i][j]%3); 40 else printf("%d ",c[i][j]%3); 41 } 42 } 43 return 0; 44 }
看其他题解
这个题有两种解法,一种是先对矩阵进行%3,
然后在3次方循环里判断如果元素如果是0,则continue不进行乘积的累加的结果。能起到优化的作用。
还有一种就是对矩阵进行某一个进行转置后,再进行两个矩阵的乘积累加。也能起到优化。
代码:
1 #include<iostream> 2 #include<cstring> 3 #include<cmath> 4 #include<cstdio> 5 #include<algorithm> 6 using namespace std; 7 int a[805][805],b[805][805],c[805][805]; 8 9 int main(){ 10 int n; 11 while(~scanf("%d",&n)){ 12 for(int i=0;i<n;i++) 13 for(int j=0;j<n;j++){ 14 scanf("%d",&a[i][j]); 15 a[i][j]%=3; 16 c[i][j]=0; 17 } 18 for(int i=0;i<n;i++) 19 for(int j=0;j<n;j++){ 20 scanf("%d",&b[i][j]); 21 b[i][j]%=3; 22 } 23 for(int i=0;i<n;i++) 24 for(int j=0;j<n;j++) 25 swap(b[i][j],b[j][i]);//转置优化 26 for(int i=0;i<n;i++) 27 for(int j=0;j<n;j++){ 28 //if(!a[i][j])continue; 29 for(int k=0;k<n;k++) 30 c[i][k]=c[i][k]+a[i][j]*b[j][k]; 31 } 32 for(int i=0;i<n;i++){ 33 for(int j=0;j<n;j++) 34 if(j==n-1)printf("%d\n",c[i][j]%3); 35 else printf("%d ",c[i][j]%3); 36 } 37 } 38 return 0; 39 }
用转置的话,也可以继续用3次方循环里判断元素是否为0,continue来优化。
直接判断的优化,时间跑1279MS,用转置不用判断是1653MS,用转置也用判断是1482MS,emnnnn。。。
1 for(int i=0;i<n;i++) 2 for(int j=0;j<n;j++){ 3 for(int k=0;k<n;k++) 4 c[i][k]=c[i][k]+a[i][j]*b[j][k]; 5 }
如果是按这种循环写,不管有没有在3次方循环里判断元素是否为0,或者不管有没有转置,都不会超时!!!
然后就是还发现了一个问题,如果三层循环里面写的是c[i][j]的循环会超时的。
1 for(int i=0;i<n;i++) 2 for(int j=0;j<n;j++){ 3 for(int k=0;k<n;k++) 4 c[i][j]=c[i][j]+a[i][k]*b[k][j]; 5 }
这个题简直有毒啊。
不管是直接判断优化还是转置优化,还是转置+判断优化,都是超时。
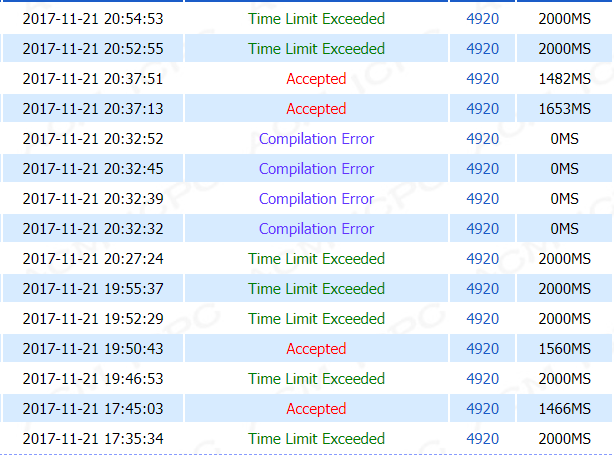
在经过这么多次智障操作之后(之后又交了一发,一共23次),并且在记录了循环的次数之后!!!
我发现。。。
1 int num=0; 2 for(int i=0;i<n;i++) 3 for(int j=0;j<n;j++){ 4 //if(!a[i][j])continue; 5 for(int k=0;k<n;k++){ 6 c[i][k]=c[i][k]+a[i][j]*b[j][k]; 7 num++; 8 } 9 }
在都不经过优化的情况下,num的次数都是一样的,两个循环的次数都是一样的。
为什么一个可以过,一个就超时呢???(所有的都测过了_(:з」∠)_ )
未解之谜啊啊啊啊啊啊啊啊啊啊啊啊啊啊_(:з」∠)_
玩不了玩不了。。。
由于C与C++的二维数组是以行为主序存储的。
因此矩阵a的行数据元素是连续存储的,而矩阵b的列数据元素是不连续存储的(N*1的矩阵除外),
为了在矩阵相乘时对矩阵b也连续读取数据,根据局部性原理对矩阵b进行转置。
然而并没有什么用,在不转置的情况下,c[i][k]的是两个按行的,c[i][j]是一个按行的。c[i][k]比c[i][j]快我可以理解。但是!!!
转置之后,c[i][k]是两个按列的,c[i][j]是一个按行的,按道理应该是c[i][j]的快啊,但是为什么还是c[i][k]]快啊。
啊啊啊啊啊啊啊,玩不了玩不了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号