2024年10月29日,在读一篇长序列预测&时空预测的综述的博客,记录一下自己需要的内容。
原博客链接:「万字长文」长序列预测 & 时空预测,你是否被这些问题困扰过?一文带你探索多元时间序列预测的研究进展!
论文:Exploring Progress in Multivariate Time Series Forecasting: Comprehensive Benchmarking and Heterogeneity Analysis
GitHub:https://github.com/GestaltCogTeam/BasicTS
TKDE 2023的综述论文。
以下为具体内容:
1. 以长序列预测为例,相关工作通常在归一化之后的数据上计算MAE、MSE,其误差非常小,只有零点几,但是把预测结果反归一化回原来的尺度上,并计算MAPE、WAPE等更直观的相对指标的时候,误差能达到百分之几十,差距非常大。
因此更合理的选择是,在报告上述指标的同时,计算MAPE、WAPE等相对误差指标,甚至同时计算反归一化之后的MAE和MSE,可以更直观地从数值中理解预测结果的好坏。
2. 模型数据处理阶段对原始时间序列数据进行归一化,采用Min-Max归一化和Z-Score归一化,每种方法对预测性能的影响不同。训练流程阶段,许多研究使用了带掩码的MAE损失函数进行模型训练,这种方法排除了异常值,避免了异常值对正常值预测的不利影响。相反,一些研究采用了简单的MAE作为优化函数,通常会导致较差的结果。此外,训练技巧的加入,如梯度剪裁和课程学习,也会显著影响性能。然而,这些配置却经常不会在论文中提及。
3. 多变量时间序列(MTS)数据集的异质性:

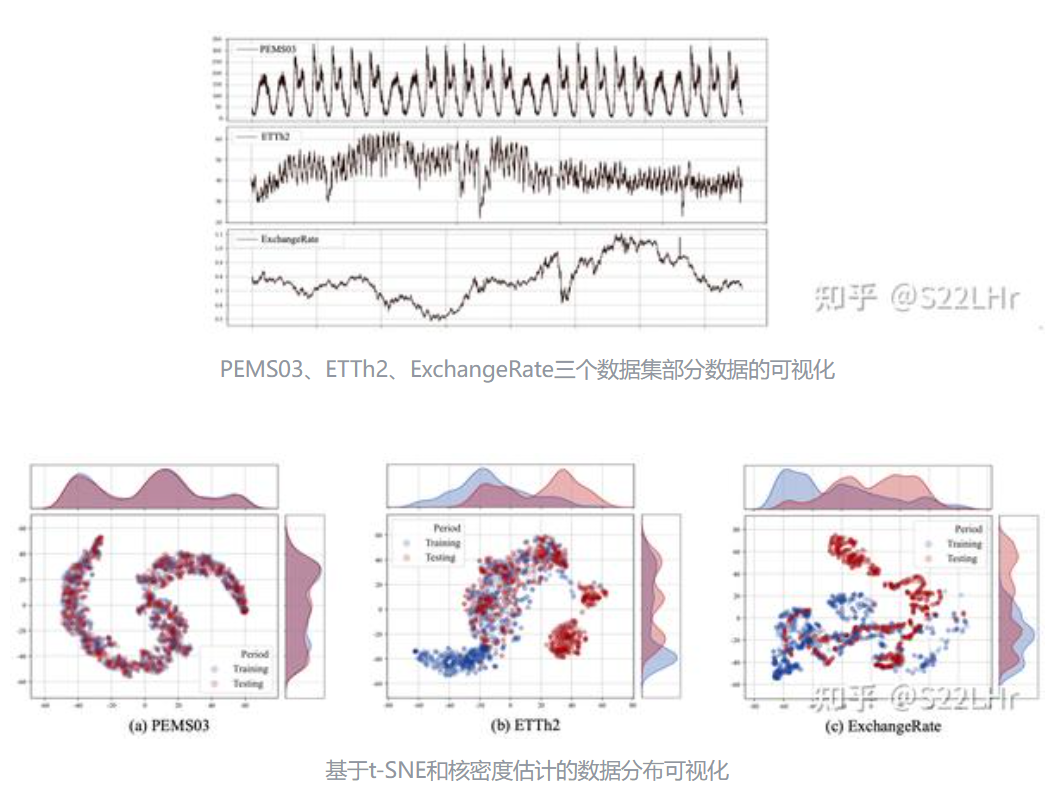
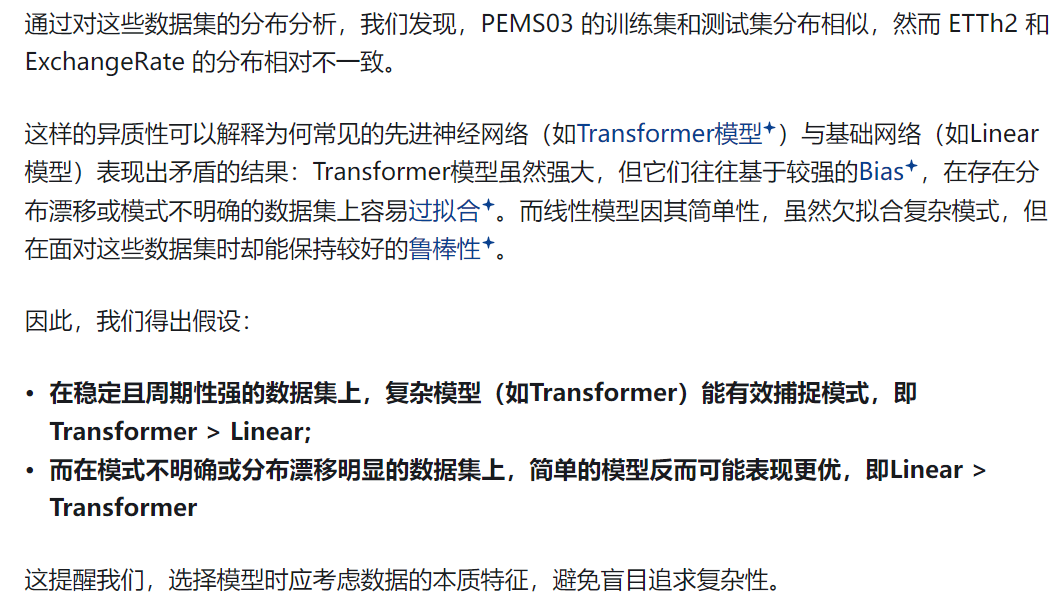
4. 相比时间维度,空间依赖关系更难以理解和量化,提出了空间不可区分性这个概念,揭示空间依赖的核心问题。空间不可区分性意味着在某个时刻,历史数据相似但未来数据不同,普通的回归模型(如MLP或更复杂的Transformer)无法通过相似的历史数据准确预测出不同的未来——即不可区分。
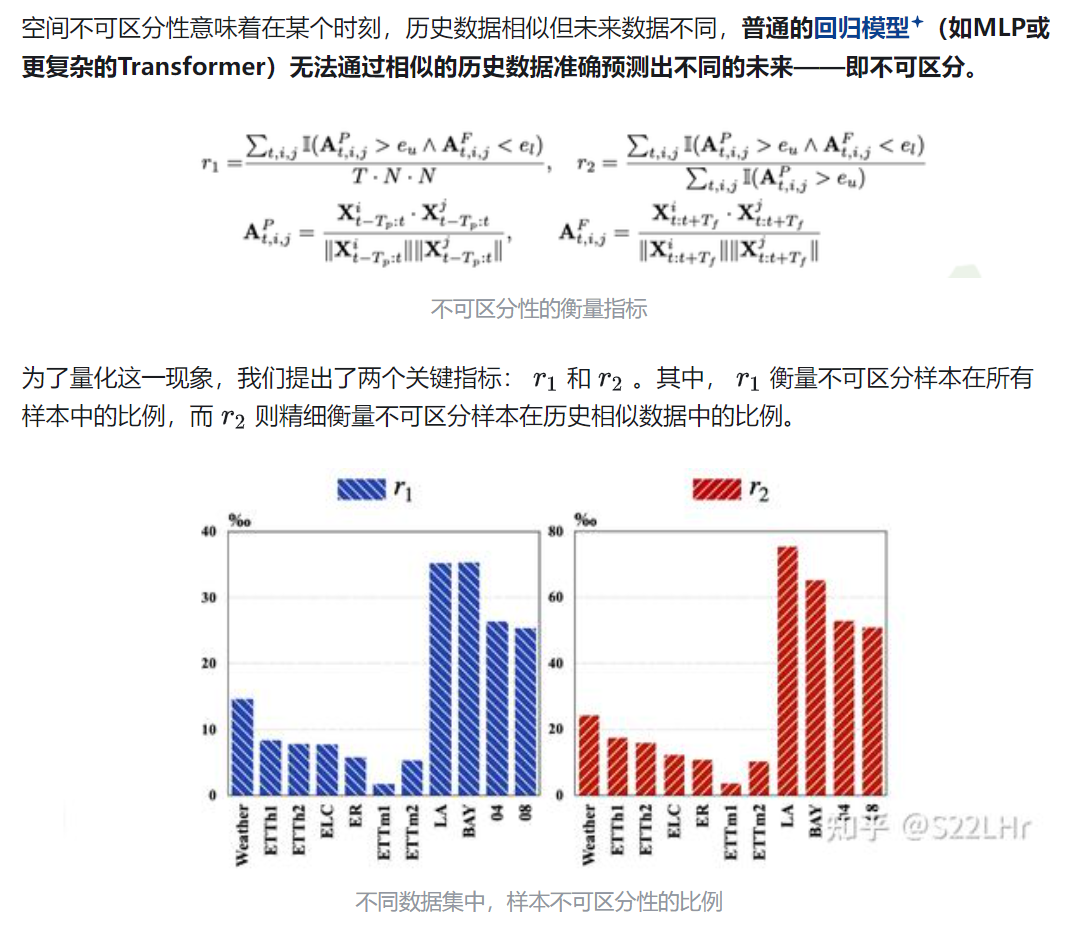

5.
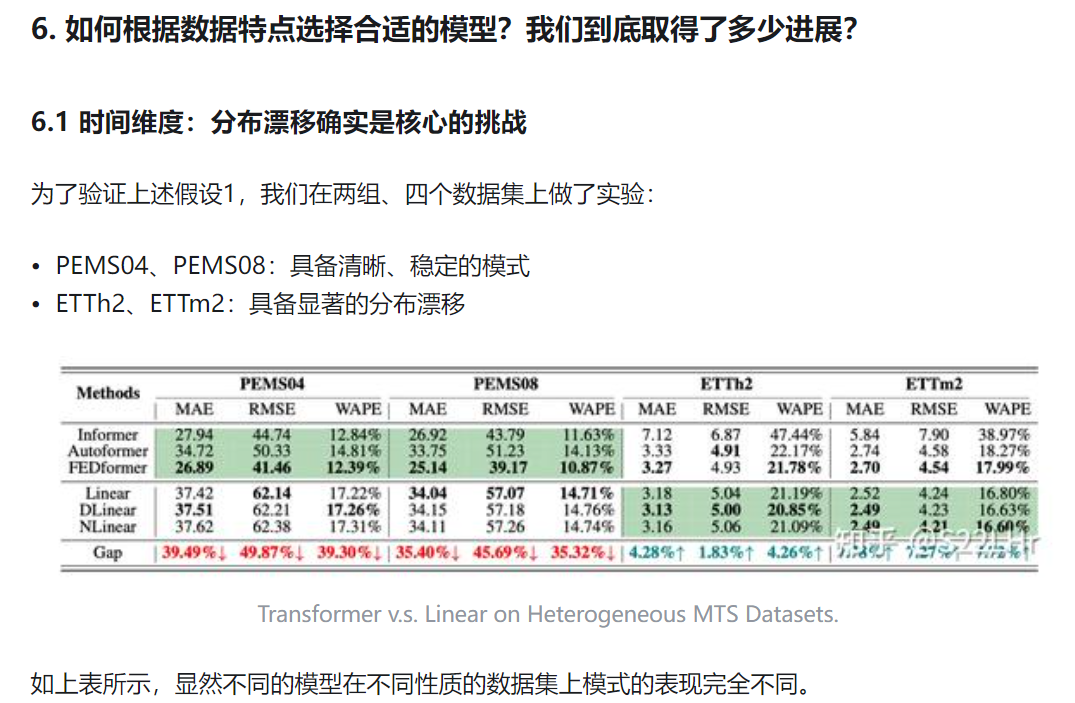
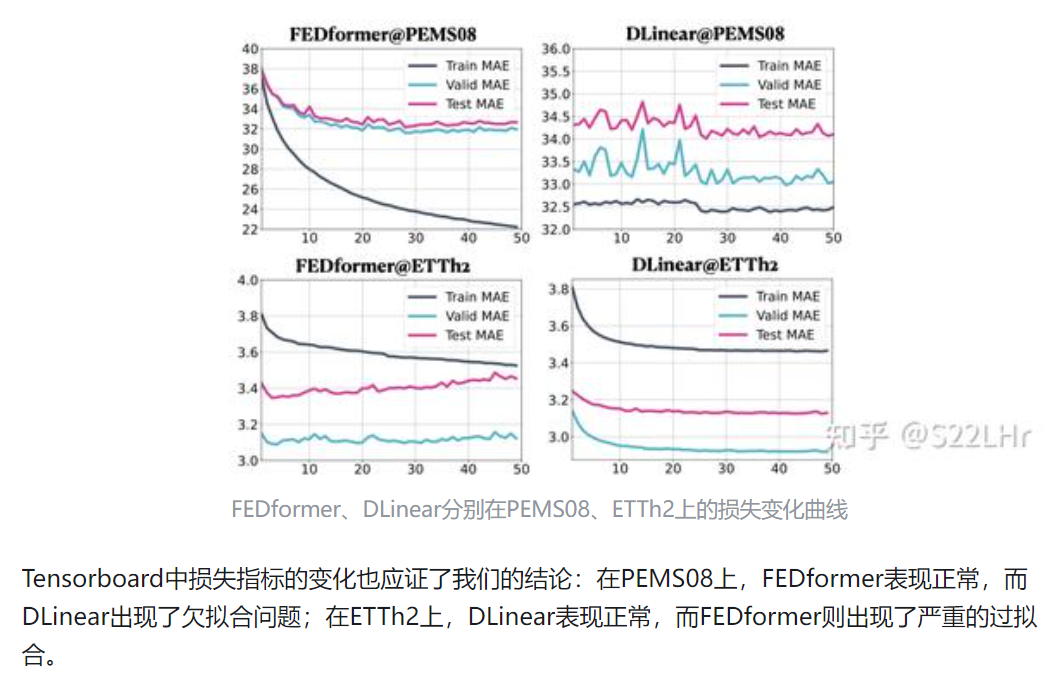
6.
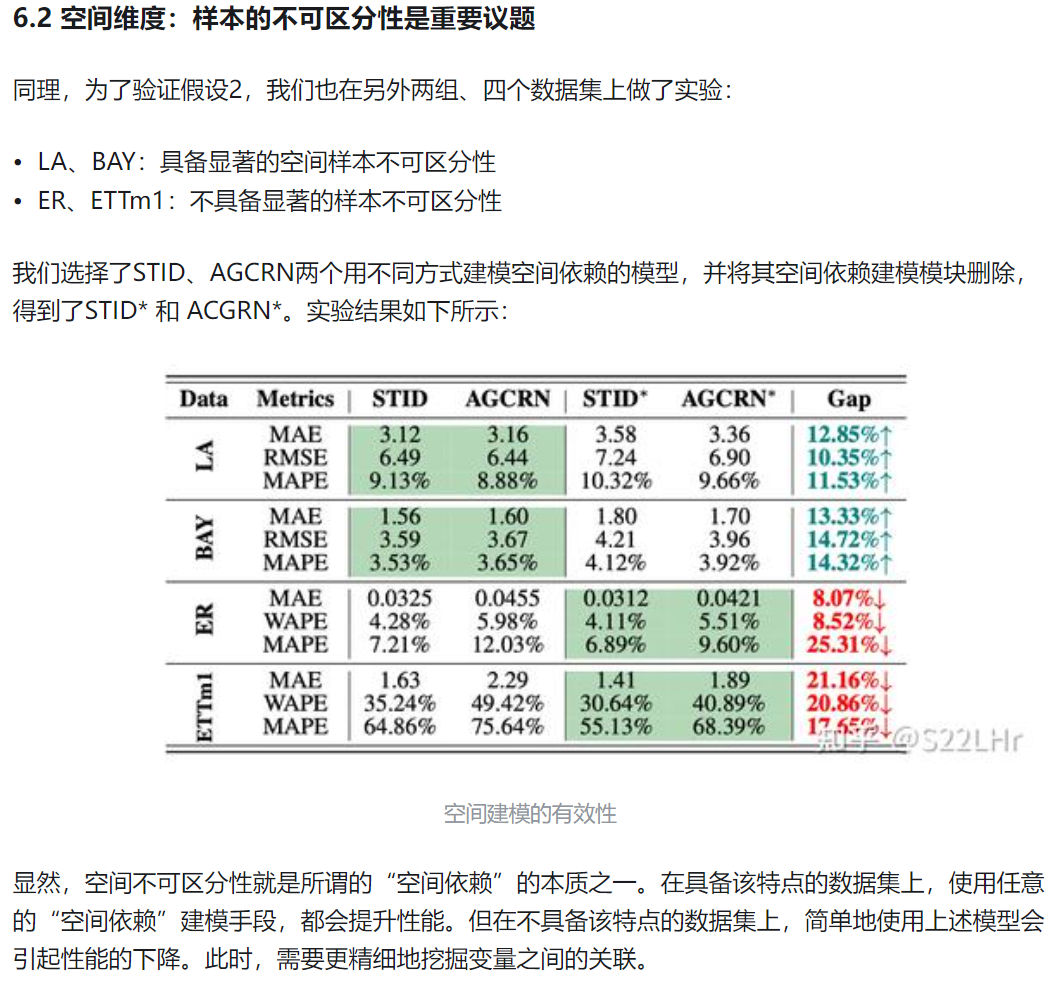
7.

8.


以下为个人(个人与GPT沟通)的一些理解和观点(可能不正确,瞎扯):
1.
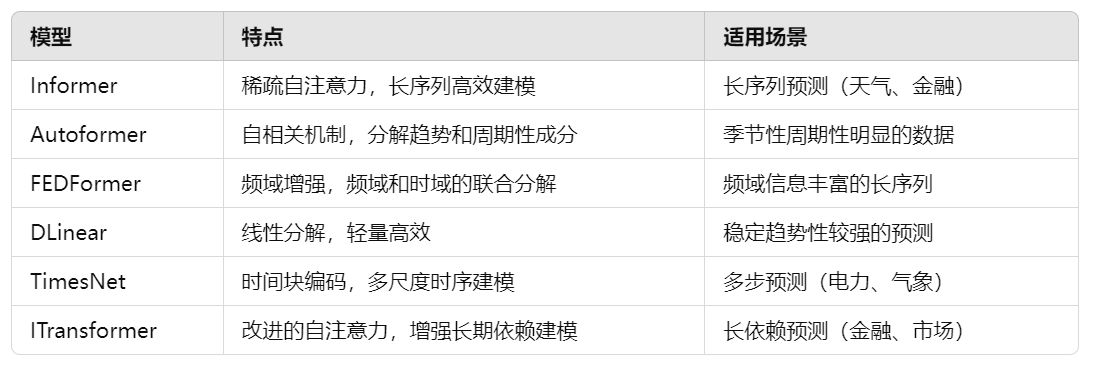
2. 时序数据的分布漂移
分布漂移(Distribution Shift)是指时间序列数据的统计分布随时间发生变化的现象。在时序数据分析中,分布漂移是一个重要的挑战,因为它会导致模型对未来数据的预测不准确,甚至完全失效。分布漂移常见于金融市场、气象、交通流量等应用中,在这些领域中,数据的特征往往随时间而改变。
1. 分布漂移的类型
分布漂移可分为不同类型,主要包括以下几类:
a. 协变量漂移(Covariate Shift)
协变量漂移是指特征变量的分布发生了变化,而目标变量的分布没有发生变化。例如在股票市场中,宏观经济指标的分布可能会随时间改变,但投资回报率的关系可能保持不变。在这种情况下,模型可能因为特征分布的改变而预测不准确。
b. 概念漂移(Concept Drift)
概念漂移是指目标变量的分布随时间变化,导致特征和目标之间的关系改变。例如在客户行为预测中,消费者的偏好随季节变化,模型需要调整才能捕捉新的关系。这种漂移可能是逐渐发生的(渐变漂移),也可能是突然的(突变漂移)。
c. 标签漂移(Label Shift)
标签漂移指的是目标变量的边际分布发生了变化,而特征分布保持不变。标签漂移在时序数据中较少见,但在某些异常检测或分类任务中会发生。例如在疾病监测中,特定疾病的流行率可能随季节变化而变化。
2. 分布漂移的成因
- 环境变化:例如季节变化、政策调整会影响数据的生成过程。
- 用户行为改变:用户偏好、需求等随时间发生变化,导致数据分布漂移。
- 系统更新或升级:在工业和生产环境中,数据生成设备的更新、检测设备的精度提高等也会引起分布漂移。
3. 分布漂移对时序模型的影响
分布漂移对时序模型的影响可能体现在以下几个方面:
- 预测精度下降:模型在训练集上的表现无法延续到测试集,因为数据分布的变化导致模型在新的数据上表现不佳。
- 模型稳定性降低:模型需要频繁更新才能适应新数据,增加了维护成本。
- 增加训练难度:分布漂移可能会导致模型在训练过程中出现较大的偏差,影响模型的收敛性。
4. 应对分布漂移的方法
应对分布漂移的方法主要有以下几种:
a. 模型重训练(Retraining)
定期收集新数据并对模型进行重训练,是应对分布漂移最直接的方法。通过更新模型参数,使得模型更好地适应当前的数据分布。然而,重训练的频率需要根据漂移的频率和幅度来平衡模型的维护成本。
b. 自适应模型(Adaptive Models)
自适应模型能够在线更新参数,以动态地调整模型对漂移的适应。例如使用在线学习方法(如自适应神经网络、贝叶斯更新)逐步调整模型。
c. 漂移检测方法
使用漂移检测算法可以识别分布漂移的发生。例如:
- 监控统计量:监控特征和目标变量的统计量(如均值、方差),识别分布的变化。
- 漂移检测算法:如Kullback-Leibler(KL)散度、Kolmogorov-Smirnov(KS)测试、Page-Hinkley检测等,检测新数据和历史数据之间的分布差异。
d. 领域自适应方法(Domain Adaptation)
如果有先验知识,模型可以通过领域自适应方法对新的分布进行调整。例如使用迁移学习,在目标领域的数据较少时,可以借助源领域的数据来进行微调。
5. 实际应用中的分布漂移实例
- 金融市场:金融市场中,经济事件、政策变化都会引起数据分布的改变,因此股票和期货预测模型需经常更新。
- 电力负荷预测:随着季节变化和能源政策的调整,电力负荷的分布会发生变化,导致原有的预测模型失效。
- 医疗诊断:随着新病原体的出现和季节变化,疾病流行情况会发生变化,因此诊断模型也需随时间调整。
总结
分布漂移是时间序列数据中不可忽视的现象,尤其在需要高精度预测的领域中,识别并适应分布漂移是确保模型准确性和稳定性的关键。
3. 异质性
(现在30日的22:00,没写完,明天继续吧.)
(现在10月31日8:59,继续.)
异质性在机器学习中的影响
异质性对数据分析和机器学习带来了一些挑战和机遇:
- 提高模型的适应性:需要设计更加灵活的模型,能够处理不同特征分布的子群体或个体。
- 数据聚类:异质性数据可以通过聚类或分组来建模,将异质性转换为不同群体或类别的分布。
- 个性化建模:在推荐系统、个性化广告等应用中,利用异质性可以为不同个体量身定制模型和方案。
- 领域自适应:在迁移学习和领域自适应中,异质性会导致源领域和目标领域的分布差异,需进行领域对齐或自适应处理。
应对异质性的常用方法
- 分群或分层分析:将数据分为多个组,分别进行分析。例如在市场分析中,可以按用户偏好进行分组。
- 多任务学习:在多任务学习中,模型通过共享部分参数,同时考虑各任务的异质性,从而提高建模效果。
- 领域自适应技术:在源和目标域之间存在异质性时,领域自适应(如对抗性训练)可以缩小它们的分布差异。
- 个性化模型:在个体异质性较强的场景下,可以使用个性化的模型或推荐系统,以更好地适应每个用户的特点。
4.
1.归一化的概念
归一化是将数据映射到一个特定的范围(通常为 [0,1]或 [−1,1]),以减少特征之间的数量级差异,从而加速模型的训练收敛。常见的归一化方法有:
-
Min-Max 归一化:将数据缩放到特定范围 [0,1][0, 1][0,1] 或 [−1,1][-1, 1][−1,1]:
xnorm=(x−xmin)/(xmax−xmin)
-
标准化(Z-score Normalization):将数据调整为均值为0,方差为1的标准正态分布:
xnorm=(x−μ)/σ
其中,μ和 σ分别为均值和标准差。
-
对数归一化:取对数缩小数据范围,用于处理具有长尾分布的数据。
2. 反归一化的概念
反归一化是归一化的逆过程,用于将模型输出的预测值还原到原始数据的尺度。例如,在回归任务中,模型的预测值经过反归一化后可以映射回原始的物理或实际量纲(如温度、价格等)。反归一化的公式通常根据归一化方法确定:
-
对于 Min-Max 归一化:
xoriginal=xnorm×(xmax−xmin)+xmin
-
对于标准化:
xoriginal=xnorm×σ+μ
5. 注意事项
归一化虽然能带来显著的好处,但在应用中需要注意:
- 归一化与反归一化的保持一致性:归一化和反归一化使用的参数(如 μ、σ、xmin、xmax等)应保持一致,确保预测结果的反归一化准确。
- 训练集和测试集归一化:通常只使用训练集的统计特征来归一化训练集和测试集,以避免信息泄漏。
- 对不同分布的数据选择合适的方法:例如,长尾分布的数据适合对数归一化,而周期性变化的数据适合标准化。
道阻且长,行则将至,行而不辍,未来可期。














