STEP: 用于多变量时间序列预测的预训练增强时空图神经网络《Pre-training Enhanced Spatial-temporal Graph Neural Network for Multivariate Time Series Forecasting》(时间序列预测)

2023年12月27日，看一篇老师给的论文。

论文：Pre-training Enhanced Spatial-temporal Graph Neural Network for Multivariate Time Series Forecasting

或者是：Pre-training Enhanced Spatial-temporal Graph Neural Network for Multivariate Time Series Forecasting

GitHub：https://github.com/zezhishao/STEP

KDD 2022的论文。

 

摘要

多变量时间序列（MTS）预测在广泛的应用中发挥着重要作用。最近，时空图神经网络（STGNNs）日益成为流行的 MTS 预测方法。STGNNs 通过图神经网络和序列模型对 MTS 的空间和时间模式进行联合建模，大大提高了预测精度。但受限于模型的复杂性，大多数 STGNN 只考虑短期的 MTS 历史数据，如过去一小时内的数据。然而，时间序列的模式和它们之间的依赖关系（即时间和空间模式）需要基于长期历史 MTS 数据进行分析。为了解决这个问题，我们提出了一个新颖的框架，其中 STGNN 由一个可扩展的时间序列预训练模型（STEP）来增强。具体来说，我们设计了一个预训练模型，从长期历史时间序列（如过去两周）中有效地学习时间模式，并生成分段级表征。这些表征为 STGNN 的短期时间序列输入提供了上下文信息，并有助于对时间序列之间的依赖关系进行建模。在三个公开的真实世界数据集上进行的实验表明，我们的框架能够显著增强下游 STGNN，而且我们的预训练模型能够恰当地捕捉时间模式。

1 引言

从交通、能源到经济，多变量时间序列数据在我们的生活中无处不在。它包含多个相互关联变量的时间序列。根据历史观测结果预测未来趋势对于帮助做出更好的决策具有重要价值。因此，几十年来，多变量时间序列预测一直是学术界和工业界经久不衰的研究课题。

事实上，多变量时间序列一般可以形式化为时空图数据 [36]。一方面，多变量时间序列具有复杂的时间模式，如多重周期性。另一方面，由于变量之间存在潜在的相互依赖关系，不同的时间序列会影响其他时间序列的演化过程，而这种相互依赖关系是非欧几里得的，可以用图结构进行合理建模。以交通流系统为例进行说明，每个传感器对应一个变量。图 1(a) 描述了部署在道路网络上的两个传感器生成的交通流时间序列。显然，有两种重复的时间模式，即每日周期和每周周期。早晚高峰每天都会出现，而工作日和周末则表现出不同的模式。此外，这两个时间序列的趋势非常相似，因为所选传感器20和301在交通网络中紧密相连。因此，准确的时间序列预测不仅取决于其时间维度的模式，还取决于其相互关联的时间序列。此外，值得注意的是，我们是在观察足够长的时间序列的基础上进行上述分析的。

为了做出准确的预测，时空图神经网络（STGNNs）最近引起了越来越多的关注。STGNNs 结合了图神经网络 (GNNs) [18] 和序列模型。前者用于处理时间序列之间的依赖关系，后者用于学习时间模式。得益于对空间和时间模式的联合建模，STGNNs 取得了最先进的性能。此外，最近越来越多的研究都在进一步探索图结构和 STGNNs 的联合学习，因为时间序列之间的依赖图是由先验知识手工绘制的，往往存在偏差和错误，在很多情况下甚至是缺失的。总之，时空图神经网络在许多实际应用中的多变量时间序列预测方面取得了重大进展。然而，天下没有免费的午餐。更强大的模型需要更复杂的结构。计算复杂度通常会随着输入时间序列长度的增加而线性或二次增加。再考虑到时间序列的数量（如数百个），STGNNs 要扩展到非常长期的历史时间序列并不容易。事实上，大多数模型都使用小窗口中的历史数据进行预测，例如，使用过去十二个时间步长（一小时）来预测未来十二个时间步长[20, 29, 35, 36, 41]。无法明确地从长期信息中学习会带来一些直观的问题。

首先，STGNN 模型对窗口之外的上下文信息视而不见。考虑到时间序列通常存在噪声，该模型可能难以区分不同背景下的短期时间序列。例如，当观察图 1(b) 所示长度为 12 的两个小窗口内的数据时，我们会发现不同背景下的两个时间序列是相似的。因此，模型很难根据有限的历史数据对它们不同的未来趋势做出准确预测。其次，短期信息对于依赖关系图的建模是不可靠的，而依赖关系图是由时间序列之间的相似性（或相关性）来表示的。如图 1（c）所示，当我们观察小窗口内的数据时，两个时间序列无论是在数量上还是在趋势上都不相似。相反，长期历史时间序列有利于抵抗噪声，从而获得更稳健、更准确的依赖关系。虽然长期历史信息是有益的，但如上所述，STGNNs 直接扩展到非常长期的历史时间序列的成本很高。此外，随着输入序列长度的增加，模型的优化也会出现问题。

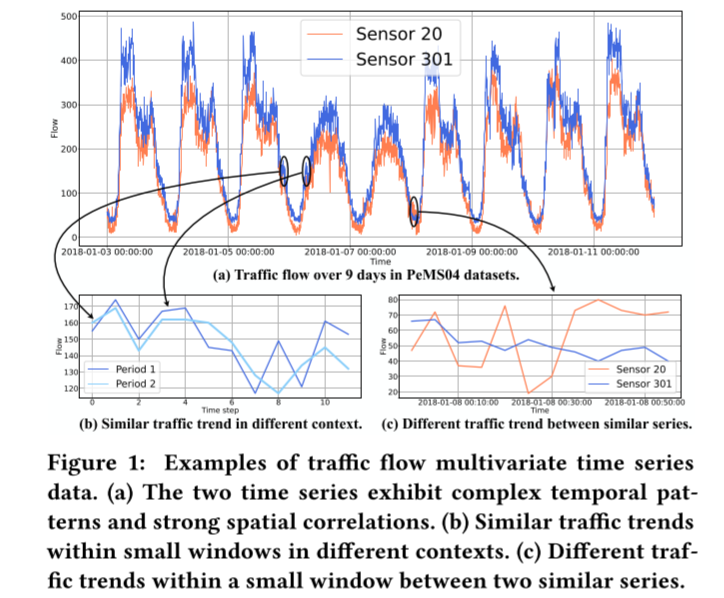
图 1：交通流多元时间序列数据示例。(a) 两个时间序列表现出复杂的时间模式和强烈的空间相关性。(b) 不同背景下小窗口内的相似交通趋势。(c) 两个相似序列之间小窗口内的不同交通趋势。

为了应对这些挑战，我们提出了一个新颖的框架，其中 STGNN 由一个可扩展的时间序列预训练模型（STEP）来增强。预训练模型旨在从非常长期的历史时间序列中有效地学习时间模式，并生成分段级表征，其中包含丰富的上下文信息，有利于应对第一个挑战。此外，这些分段（即短期时间序列）的学习表示能够结合整个长期历史时间序列的信息来计算时间序列之间的相关性(怎么整合的，好奇)，从而解决第二个挑战，即依赖图缺失的问题。具体来说，我们设计了一种基于 TransFormer 块[33]的高效时间序列无监督预训练模型（TSFormer），该模型通过掩码自动编码策略[13]进行训练。TSFormer 能有效捕捉数周以上的长期历史数据信息，并生成能正确反映时间序列复杂模式的分段级表示。其次，我们设计了基于 TSFormer 表示的图结构学习器，它可以学习离散依赖图，并利用基于 TSFormer 表示计算的𝑘NNN 图作为正则化，指导图结构和 STGNN 的联合训练。值得注意的是，STEP 是一个通用框架，几乎可以扩展到任意 STGNN。总之，其主要贡献如下：

• 我们提出了一种新颖的多元时间序列预测框架，通过预训练模型来增强 STGNN。具体来说，预训练模型生成包含上下文信息的分段级表征，以改进下游模型。
• 我们设计了一种基于 Transformer 块的高效无监督时间序列预训练模型，并通过掩码自动编码策略对其进行训练。此外，我们还设计了一种图结构学习器来学习依赖图。
• 在三个真实世界数据集上的实验结果表明，我们的方法能显著提高下游 STGNN 的性能，而且我们的预训练模型能恰当地捕捉时间模式。

2 前言

我们首先定义了多变量时间序列的概念，依赖图。然后，我们定义所要解决的预测问题。

定义 1. 多元时间序列。多元时间序列包含多个时间变量，例如来自多个传感器的观测数据。它可以表示为一个张量 X∈R𝑇×𝑁×𝐶 ，其中𝑇 是时间步数，𝑁 是变量（如传感器）的数量，𝐶 是通道的数量。此外，我们还将时间序列 𝑖 的数据表示为 S𝑖∈ R𝑇×𝐶 。

定义 2. 依赖图。每个变量不仅取决于其过去的值，还取决于其他变量。这种依赖关系由依赖图 G = (𝑉, 𝐸)来捕捉，其中 𝑉 是 |𝑉| = 𝑁 节点的集合，每个节点对应一个变量，如传感器。𝐸是|𝐸| = 𝑀边的集合。图也可表示为相邻矩阵 A∈R𝑁×𝑁 。

定义 3. 多元时间序列预测。多变量时间序列预测的目的是预测最接近未来时间步长的𝑇𝑓的值 Y∈R𝑇×𝑁×𝐶。

3 模型架构

如图 2 所示，STEP 有两个阶段：预训练阶段和预测阶段。在预训练阶段，我们设计了一个基于 TransFormer 块（TSFormer）的时间序列掩码自动编码模型，以高效地学习时间模式。TSFormer 能够从长期序列中学习，并提供包含丰富上下文信息的段级表示。在预测阶段，我们使用预训练编码器提供上下文信息，以增强下游 STGNN。此外，基于预训练模型的表征，我们进一步设计了离散稀疏图学习器，以处理预定义图缺失的情况。

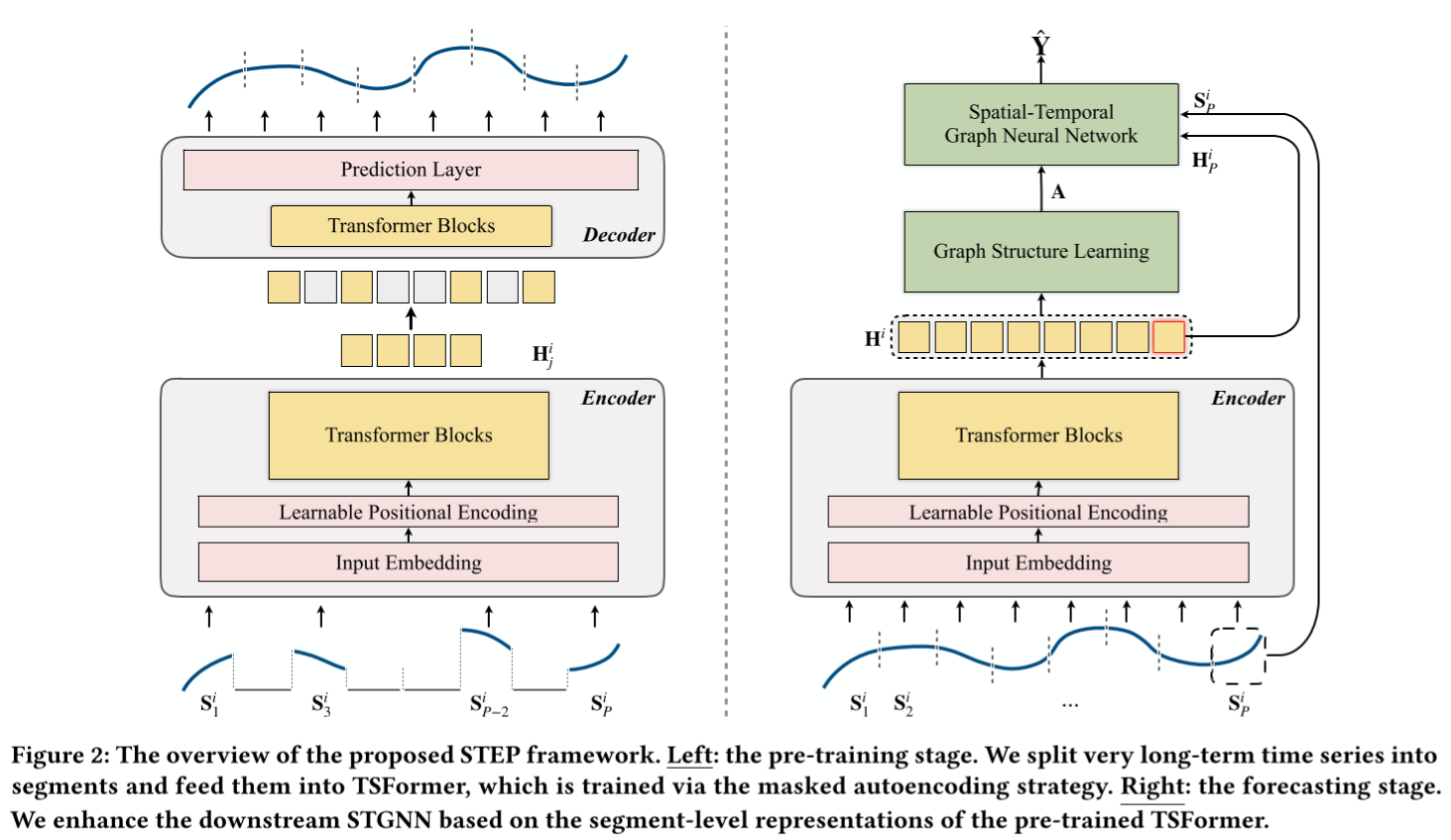
图 2：拟议的 STEP 框架概览。左图：预训练阶段。我们将非常长期的时间序列分割成片段，并将其输入 TSFormer，通过掩码自动编码策略对其进行训练。右图：预测阶段。
我们根据预训练 TSFormer 的分段级表示来增强下游 STGNN。

3.1 预训练阶段

在这一部分，我们的目标是为时间序列设计一个高效的无监督预训练模型。虽然预训练模型在自然语言处理领域取得了重大进展[3, 8, 27]，但在时间序列领域的进展却落后于它们。首先，我们想讨论一下时间序列与自然语言之间的区别，这将为 TSFormer 的设计提供灵感。我们试图从以下两个角度来区分它们：

(i) 时间序列信息密度较低。作为人类生成的信号，自然语言中的每个数据点（即句子中的一个词）都具有丰富的语义，适合作为模型输入的数据单元。相反，时间序列中孤立的数据点提供的语义信息较少。只有当我们观察到至少分段级的数据（如上升或下降）时，才会产生语义。另一方面，语言模型通常是通过预测每个句子中的几个缺失词来进行训练的。然而，时间序列中的屏蔽值往往可以通过简单的插值预测出来[39]，这使得预训练模型只关注低层次信息。为了解决这个问题，一种简单而有效的策略是，根据计算机视觉的最新发展[13]，对模型输入的很大部分进行屏蔽，以鼓励学习高层语义。它创建了一个具有挑战性的自监督任务，迫使模型获得对时间序列的整体理解。

(ii) 时间序列需要更长的序列来学习时间模式。在自然语言中，数百个长度的序列包含丰富的语义信息。因此，语言预训练模型通常会将输入序列剪切或填充为数百条 [3, 8, 27]。然而，虽然时间序列的语义比自然语言相对简单，但却需要更长的序列来学习。例如，交通系统每五秒记录一次数据，如果我们想学习每周的周期性，至少需要连续的 2016 个时间片。虽然以较低的频率采样是一种可行的解决方案，但它不可避免地会丢失信息。幸运的是，虽然较长的时间序列会增加模型的复杂性，但我们可以通过减少 Transformer 块的堆叠来缓解复杂性，并在预测阶段固定模型参数，以减少计算和内存开销。

受上述分析和最近的计算机视觉模型[9]，特别是掩码自动编码器（MAE）[13]的启发，我们提出了一种基于 Transformer 块的时间序列掩码自动编码模型（即 TSFormer）。TSFormer 基于给定的部分观测信号重建原始信号。我们采用非对称设计来大大减少计算量：编码器只对部分可见信号进行操作，而解码器则对全部信号使用轻量级网络。模型如图 2（左）所示，接下来我们将详细介绍每个组件。

Masking. 我们将来自节点 𝑖 的输入序列 S𝑖 分成长度为 𝑃 的非重叠片段（输入序列通过长度为 𝑃 ∗𝐿 的滑动窗口在原始时间序列上获取）。第 𝑗 个补丁可以表示为 S𝑖𝑗 ∈ R𝐶𝐿，其中 𝐶 是输入通道。我们假设𝐿 是 STGNNs 输入时间序列的常用长度。我们随机掩码了一个补丁子集，掩蔽率 𝑟 设为 75%，以创建一个具有挑战性的自监督任务。在此，我们强调，将补丁作为输入单元的策略有多重目的。首先，片段（如补丁）比单独的点更适合明确提供语义。其次，它有利于下游模型的使用，因为下游 STGNN 将单个片段作为输入。最后但并非最不重要的一点是，它大大减少了输入编码器的序列长度，而且高掩蔽率 𝑟 使编码器在预训练阶段更加高效。

Encoder. 我们的编码器是一系列带有输入嵌入层和位置编码层的 Transformer 模块[33]。编码器只对未掩码的补丁进行处理。由于时间序列的语义比语言更直观，我们使用了四层 Transformer 块，远小于计算机视觉 [9, 13] 和自然语言 [3, 8] 中基于 Transformer 的模型的深度。具体来说，输入嵌入层是一个线性投影，用于将未掩码的补丁转换到潜在空间：

其中，W∈R𝑑×（𝐶𝐿）和 b∈R𝑑 是可学习参数，U𝑖 (1) 𝑗∈R𝑑 是模型输入向量，𝑑 是隐藏维度。对于掩码补丁，我们使用一个共享的可学习掩码标记来指示是否存在待预测的缺失补丁。接下来，位置编码层用于添加序列信息。值得注意的是，虽然编码器中不使用掩码标记，但位置编码对所有补丁都有效。此外，与 MAE [13] 中使用的确定性正弦嵌入不同，我们使用的是可学习的位置嵌入。一方面，在这项工作中，在所有数据集上，可学习嵌入都明显优于正弦嵌入。另一方面，我们观察到，学习到的位置嵌入对学习时间序列的周期特征至关重要，这将在第 4.3 节中得到证明。最后，我们通过 Transformer 模块为所有未掩码的补丁𝑗获取潜在表示 H𝑖𝑗∈R𝑑。

Decoder. 解码器也是一系列 Transformer 块，用于将潜在表征重构回较低的语义层次，即数字信息。解码器对包括掩码标记在内的全套补丁进行解码。与 MAE[13]不同的是，我们在这里不再添加位置嵌入，因为在编码器中所有补丁都已经添加了位置信息。值得注意的是，解码器只在预训练阶段用于执行序列重建任务，可以独立于编码器进行设计(好的)。为了平衡效率和效果，我们只使用了单层 Transformer 块。最后，我们使用多层感知（MLP）进行预测，其输出维数等于每个补丁的长度。具体来说，给定补丁𝑗的潜在表示 H𝑖𝑗∈ R𝑑 后，解码器给出重建序列 ˆS𝑖𝑗∈ R𝐿𝐶。

重建目标。我们的损失函数计算原始序列 S𝑖𝑗 与重建序列 Sˆ𝑖𝑗 之间的平均绝对误差。请注意，我们只计算掩码补丁的损失，这与其他预训练模型[8, 13]是一致的。此外，所有这些操作都是针对所有时间序列 𝑖 并行计算的。

总之，TSFormer 的高效得益于较高的掩码率和较少的 Transformer 块。TSFormer 能够从非常长的序列（如数周）中学习，并且可以在单个 GPU 上进行训练。编码器会生成输入补丁（片段）的表示。此外，与 MAE [13] 的另一个值得注意的不同之处在于，我们更加关注补丁的表示。一方面，我们可以使用这些表示来验证数据中的周期性模式，这将在第 4.3 节中进行演示。更重要的是，它们可以方便地充当下游 STGNN 短期输入的上下文信息，这将在下一节中介绍。

3.2 预测阶段

对于给定的时间序列𝑖，TSFormer 将其历史信号 S𝑖∈ R𝑇𝑝×𝐶 的过去 𝑇𝑝 = 𝐿 × 𝑃 时间步数作为输入。我们将其划分为长度为 𝐿 的 𝑃 个非重叠补丁： S𝑖1, ... , S𝑖𝑃，其中 S𝑖𝑗∈R𝐿×𝐶。预训练的 TSFormer 编码器为每个 S𝑖𝑗 生成 H𝑖𝑗∈ R𝑑 的表示，其中 𝑑 是隐藏状态的维度。考虑到计算复杂度通常与输入时间序列的长度成线性或二次函数关系，STGNN 只能将最新的，即每个时间序列 𝑖 的最后一个补丁 S𝑖𝑃∈ R𝐿×𝐶 作为输入。例如，最典型的设置是 𝐿 = 12。在预测阶段，我们的目标是根据预训练 TSFormer 编码器的表示来增强 STGNN。

图结构学习。许多 STGNNs [20, 36, 41] 都依赖于预先定义的图来表示节点（即时间序列）之间的关系。然而，这种图在很多情况下是不可用或不完整的。一个直观的想法是训练一个矩阵 A∈ R𝑁×𝑁，其中 A𝑖 𝑗∈ [0, 1] 表示时间序列 𝑖 和 𝑗 之间的依赖关系。然而，由于图结构和 STGNNs 的学习是紧凑耦合的，而且图结构学习没有监督损失信息[21]，优化这样一个连续矩阵通常会导致一个复杂的双层优化问题[10](双层优化问题，gpt了)。此外，依赖关系 A𝑖𝑗 通常是通过时间序列之间的相似性来衡量的，这也是一项具有挑战性的任务。

幸运的是，我们可以基于预训练的 TSFormer 来缓解这些问题。受近期研究[10, 17, 29]的启发，我们的目标是学习离散稀疏图，其中 Θ𝑖𝑗 参数化了伯努利分布，离散依赖图 A 就是从伯努利分布中采样的。首先，我们引入图正则化，为基于 TSFormer 表示的图优化提供监督信息。具体来说，我们将 H𝑖 = H𝑖 1 ∥ H𝑖 2...H𝑖 𝑃-1 ∥ H𝑖 𝑃∈ R𝑃𝑑 作为时间序列 𝑖 的特征，其中 ∥ 表示连接操作。然后，我们计算所有节点间的𝑘NN 图 A𝑎。我们可以通过设置不同的 𝑘 来控制所学图的稀疏性。得益于 TSFormer 的能力，A𝑎 可以反映节点之间的依赖关系，有助于指导图结构的训练。然后，我们按如下方法计算 Θ𝑖𝑗：

其中，Θ𝑖𝑗 ∈ R2 是非标准化概率。第一个维度表示正概率，第二个维度表示负概率。G𝑖 是时间序列 𝑖 的全局特征，由卷积网络 G𝑖 =FC(vec(Conv(S𝑖𝑡𝑟𝑎𝑖𝑛))）得出， 其中，S𝑖𝑡𝑟𝑎𝑖𝑛 ∈ R𝐿𝑡𝑟𝑎𝑖𝑛 是训练数据集的整个序列𝑖，𝑡𝑟𝑎𝑖𝑛 是训练数据集的长度。在训练过程中，S𝑖𝑡𝑟𝑎𝑖𝑛 对所有样本都是静态的(这句话，嗯？)，这有助于提高训练过程的鲁棒性和准确性。对于不同的训练样本，特征 H𝑖 是动态的，以反映依赖图的动态变化[19]。因此，我们使用 Θ 和 𝑘NN 图 𝐴𝑎 之间的交叉熵作为图结构正则化：

其中，Θ ′𝑖𝑗 = softmax(Θ𝑖𝑗 )∈ R 是归一化概率。

离散图结构学习的最后一个问题是，从 Θ 到相邻矩阵 A 的采样操作是不可微的。因此，我们采用了 [15, 25] 提出的 Gumbel-Softmax 重参数化技巧：

其中，g ∈ R2 是一个 i.i.d. 样本向量，取自 Gumbel(0,1) 分布。𝜏 是软最大温度参数。当 𝜏 → 0 时，GumbelSoftmax 会收敛到独热样本（即离散）。

(现在是2024年2月26日，13:48，鸽了两个月了，我有罪，继续看吧。)

下游时空图神经网络。普通的下游 STGNN 将最后一个补丁和依赖图作为输入，而增强型 STGNN 还考虑了输入补丁的表示。由于 TSFormer 在提取长期依赖关系方面具有很强的能力，因此表示 H𝑖𝑃 包含丰富的上下文信息。STEP 框架几乎可以扩展到任何 STGNN，我们选择了一种具有代表性的方法作为我们的后端，即 Graph WaveNet [36]。Graph WaveNet 通过将图卷积与扩张随意卷积相结合，高效捕捉空间-时间依赖关系。它通过多层感知（MLP）的回归层，根据其输出的潜在隐藏表征 H𝑔𝑤 ∈ R𝑁×𝑑′ 进行预测。为简洁起见，我们省略其细节，感兴趣的读者可参阅论文[36]。将所有节点的 TSFormer 表示 H𝑖𝑃 表示为 H𝑃∈ R𝑁×𝑑：

其中，SP(-) 是语义投影器，用于将 H𝑖 (5) 𝑃 Transformer 到 H𝑔𝑤 的语义空间。我们用 MLP 来实现它。最后，我们通过回归层进行预测： Yˆ∈ R𝑇𝑓×𝑁×𝐶. 给定地面实况 Y∈R𝑇𝑓×𝑁×𝐶 后，我们使用平均绝对误差作为回归损失：

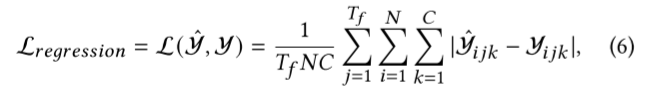
其中，𝑁 是节点数，𝑇𝑓 是预测步数，𝐶 是输出维度。下游 STGNN 和图结构以端到端的方式进行训练：

我们将图正则化项𝜆设置为在训练过程中逐渐衰减，以超越𝑘NN 图。值得注意的是，预训练的 TSFormer 编码器在预测阶段是固定的，以减少计算和内存开销。

4 实验

在本节中，我们将介绍在三个真实数据集上进行的实验，以证明所提出的 STEP 和 TSFormer 的有效性。此外，我们还进行了综合实验，以评估重要超参数和组件的影响。值得注意的是，我们对每个数据集都进行了预训练，因为这些数据集在时间序列长度、物理性质和时间模式方面都是异构的。我们的代码可在此资源库1中找到。

4.1 实验设置

数据集。根据之前的研究 [29, 35, 36]，我们在三个常用的多元时间序列数据集上进行了实验：

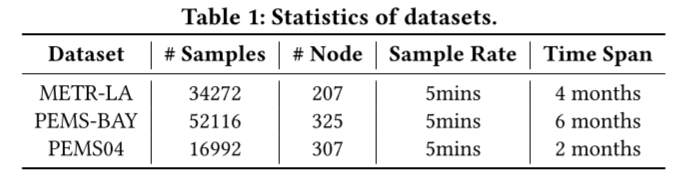
• METR-LA 是一个交通速度数据集，由洛杉矶县道路网络中的环路检测器收集[14]。它包含 207 个选定传感器在 2012 年 3 月至 6 月 4 个月期间的数据[20]。交通信息每 5 分钟记录一次，时间片总数为 34 272 个。
• PEMS-BAY 是一个交通速度数据集，收集自加州交通局（CalTrans）的性能测量系统（PeMS）[5]。它包含湾区 325 个传感器在 2017 年 1 月 1 日至 2017 年 5 月 31 日 6 个月期间的数据[20]。交通信息以每 5 分钟一次的速度记录，时间片总数为 52 116 个。
• PEMS04 是一个交通流数据集，也是从加州交通局 PeMS 系统中收集的[5]。它包含湾区 307 个传感器从 2018 年 1 月 1 日到 2018 年 2 月 28 日两个月期间的数据[11]。交通信息以每 5 分钟一次的速率记录，时间片总数为 16992 个。

统计信息汇总于表 1。为了公平比较，我们沿用了前人的数据集划分方法。对于 METR-LA 和 PEMS-BAY，我们使用约 70% 的数据进行训练，20% 的数据进行测试，剩余 10% 的数据进行验证[20, 36]。对于 PEMS04，我们使用约 60% 的数据进行训练，20% 的数据用于测试，剩余 20% 的数据用于验证 [11，12]。

基线。我们选择了大量具有官方公开代码的基线。历史平均法（HA）、VAR [23] 和 SVR [30] 是传统方法。FC-LSTM [32]、DCRNN [20]、Graph WaveNet [36]、ASTGCN [11] 和 STSGCN [31] 是典型的深度学习方法。GMAN[41]、MTGNN[35]和GTS[29]是近期最先进的作品。有关基线的更多详情，请参见附录 A.1。

指标。我们用多元时间序列预测中常用的三个指标来评估所有基线的性能，包括平均绝对误差（MAE）、均方根误差（RMSE）和平均绝对百分比误差（MAPE）。

实施。我们将补丁大小 𝐿 设为 12。我们将 METR-LA 和 PEMS-BAY 的片段数𝑃设为 168，PEMS04 的片段数𝑃设为 336，即 METR-LA 和 PEMS-BAY 使用一周的历史信息，PEMS04 使用两周的历史信息。我们的目标是预测未来 12 个时间步。掩码比率 𝑟 设为 75%。TSFormer 𝑑 潜在表示的隐藏维度设为 96。TSFormer 编码器使用 4 层 Transformer 块，解码器使用 1 层。Transformer 块中的注意力头数设置为 4。Graph WaveNet 的超参数设置为其论文 [36] 中的默认值。对于𝑘NN 图形 A𝑎，我们将𝑘设为 10。我们对所有实验结果进行显著性检验（p 值小于 0.05 的 t 检验）。

4.2 主要结果

如表 2 所示，我们的 STEP 框架在所有数据集的几乎所有时间跨度上都取得了最佳性能，这表明了我们框架的有效性。GTS 和 MTGNN 联合学习多个时间序列之间的图结构和时空图神经网络。GTS 扩展了 DCRNN，引入了邻域图作为正则化来提高图的质量，并将问题重新表述为单层优化问题。MTGNN 用混合跳转传播层 [1] 和扩张阈值层取代了图波网中的 GNN 和 Gated TCN，并提出学习潜在邻接矩阵以寻求进一步改进。然而，它们无法持续超越其他基线。请注意，GTS 的结果可能与原论文有一些差距，因为它计算评估指标的方式略有不同。一些细节可以在原论文[29]的附录中找到，类似问题也可以在其官方代码库2中找到。我们将评估过程与其他基线统一起来，运行 GTS 五次，并报告其最佳性能。GMAN 在长期预测方面表现更好，这得益于注意力机制在捕捉长期依赖性方面的强大能力。DCRNN 和 Graph WaveNet 是两种典型的时空图神经网络。即使与 ASTGCN 和 STSGCN 等许多较新的作品相比，它们的性能仍然非常可观。这可能得益于它们精炼合理的模型架构。FC-LSTM 作为一种经典的递归神经网络，由于只考虑了时间特征，忽略了时间序列之间的依赖关系，因此表现不佳。其他非深度学习方法 HA、VAR 和 SVR 的表现最差，因为它们对数据有很强的假设，如静态或线性假设。因此，它们无法捕捉现实世界数据集中强烈的非线性和动态时空相关性。

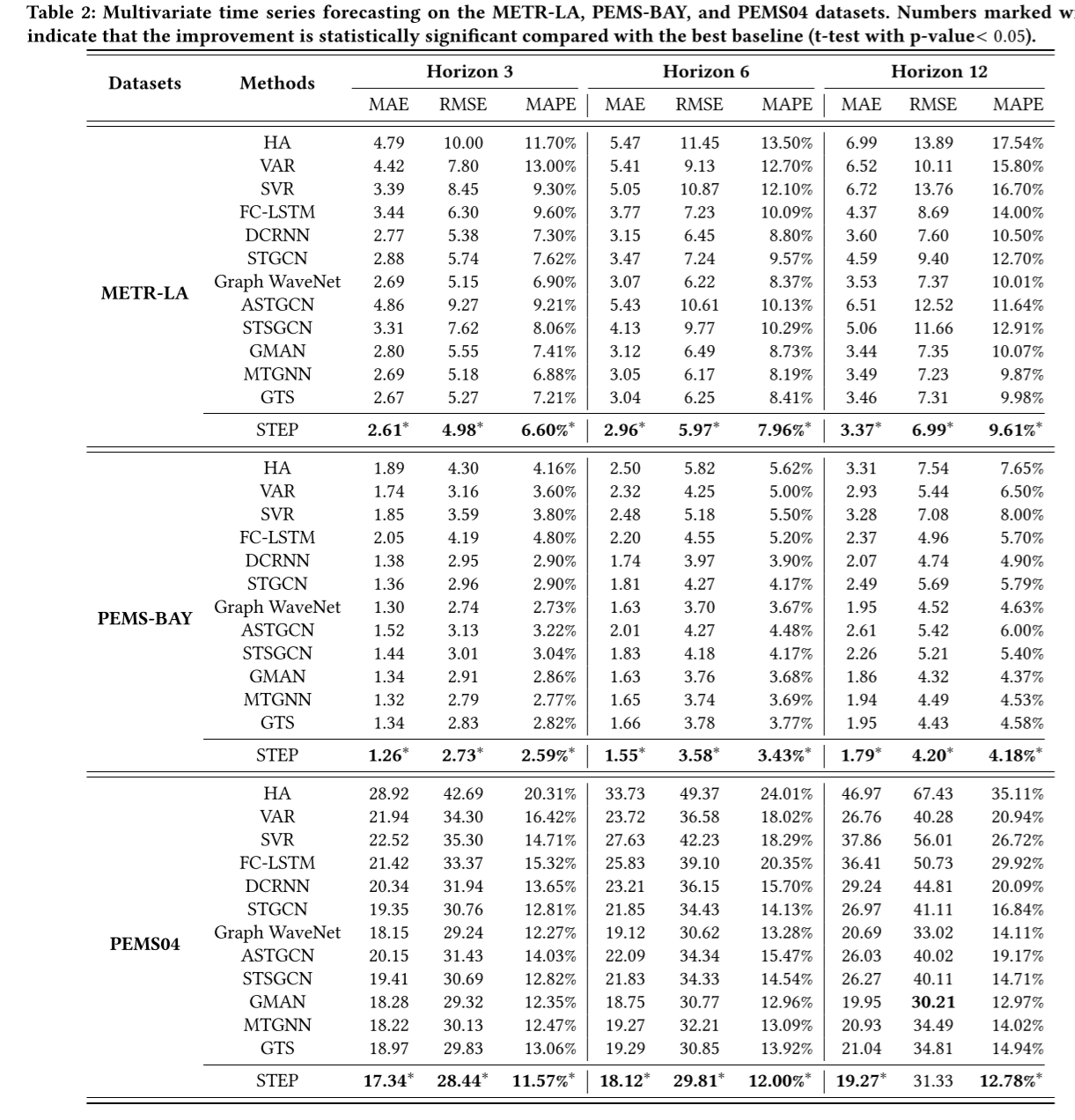
简而言之，STEP 充分利用了 TSFormer 从长期历史时间序列中提取的表征，为 Graph WaveNet 带来了稳定的性能提升。然而，尽管性能有了显著提高，我们却很难直观地理解 TSFormer 学到了什么，以及它如何帮助 STGNN。在下一小节中，我们将检查 TSFormer，并展示学习到的多周期性时间模式。

4.3 检验 TSFormer

我们在 PEMS04 数据集上进行了实验。具体来说，我们在 PEMS04 数据集中随机选择一个时间序列，然后从测试数据集中随机选择一个样本来分析 TSFormer。请注意，PEMS04 中的每个输入样本都有 336 个长度为 12 的片段，这意味着它涵盖了过去两周的数据。

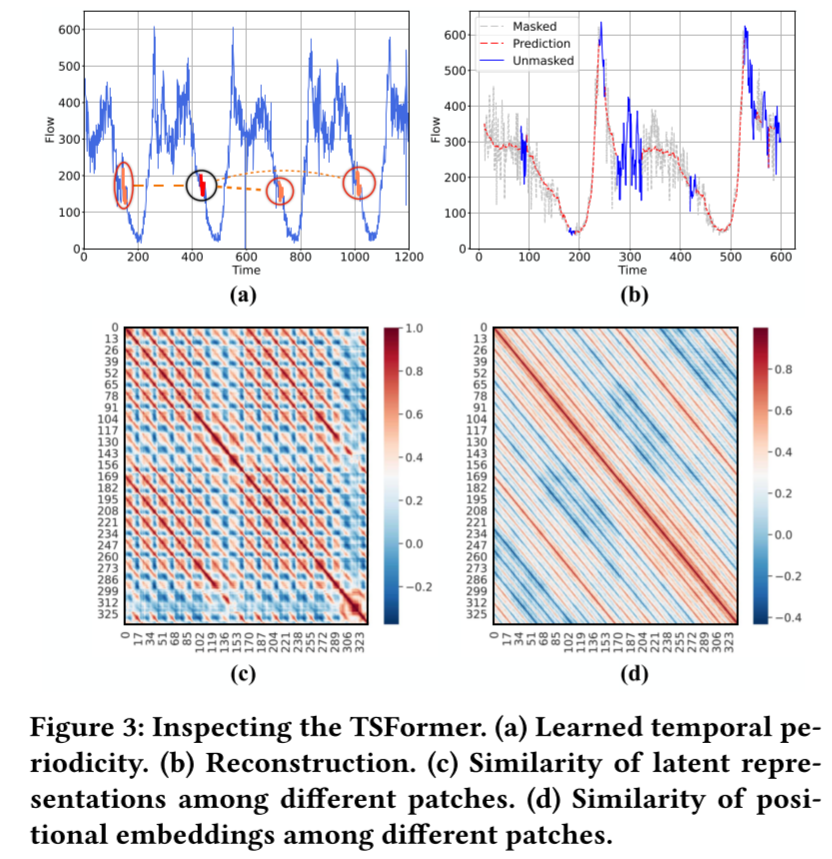
学习时间模式。我们希望它能生成有意义的表征，并能解决图 1（b）中的问题。因此，我们随机选取一个补丁，计算其与所有其他补丁的表示的余弦相似度，并选取最相似的 3 个补丁。结果如图 3(a)所示，黑色圆圈中为原始补丁，红色圆圈中为选出的最相似补丁。显然，TSFormer 有很强的识别相似补丁的能力。此外，为了获得更大的图像，我们还计算了所有补丁之间的成对相似度，并得到一个 336 × 336 的热图，其中第 𝑖 列和第𝑗 行中的元素表示补丁 𝑖 和补丁 𝑗 之间的余弦相似度。图 3(c) 中显示的结果呈现出明显的日周期和周周期。每个补丁都与一天中同一时间的补丁相似，最相似的补丁通常出现在一周中同一天的同一时间。这一观察结果符合人类的直觉。蓝色的列或行表示传感器此时瘫痪或有较大的噪声波动，这使得它与其他补丁不同。既然 TSFormer 已经学会了正确的补丁间关系，那么它能显著增强下游 STGNN 也就在情理之中了。

重建可视化。此外，我们还对 TSFormer 重建的结果进行了可视化，如图 3(b) 所示，其中灰色线条呈现的是掩码补丁，红色线条展示的是重建结果。结果表明，TSFormer 可以根据少量未掩码补丁（蓝线）有效地重建掩码补丁。

位置嵌入。TSFormer 和 MAE [13] 与最初的 Transformer [33] 的另一个重要区别是可学习的位置嵌入。因此，我们想探究一下 TSFormer 是否学习了合理的位置嵌入。我们计算了 336 个补丁的位置嵌入之间的余弦相似度，得到了 336 × 336 的热图，如图 3(d)所示。我们发现，TSFormer 的位置嵌入能更好地反映时间序列的多周期性。这是因为，编码器的表示需要依赖于输入补丁，而位置嵌入则不同，它可以完全自由地进行优化，受输入数据噪声的影响较小。我们推测，这种位置嵌入是 TSFormer 取得成功的关键因素，因为我们发现，如果用确定的正弦位置嵌入代替可学习的位置嵌入，TSFormer 就无法获得有意义的表示。

4.4 消融实验

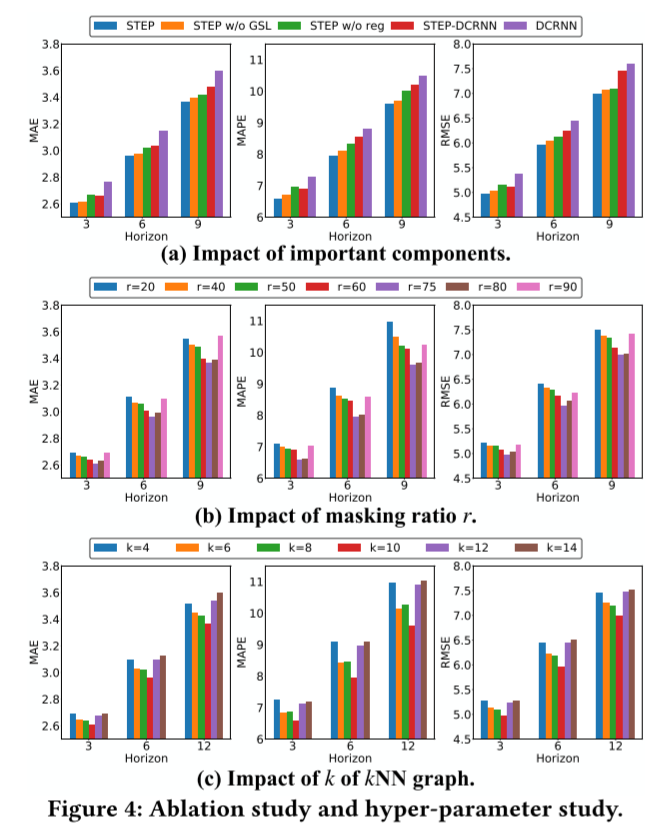
在这一部分，我们将进行实验来验证一些关键组件的影响。首先，我们设置 STEP w/o GSL 来测试不使用图结构学习模型的性能。其次，我们设置 STEP w/o reg，用 GTS[29]中基于原始时间序列 Sit𝑟𝑎𝑖𝑛 的余弦相似度计算的𝑘NNN 图替换由 TSFormer 表示法计算的𝑘NNN 图，以测试 TSFormer 长序列表示法的优越性。最后，我们还测试了更多下游 STGNN，以验证 STEP 的通用性。我们选择 DCRNN 作为另一个后端，即 STEP-DCRNN。此外，我们还对 DCRNN 的性能进行了比较。结果如图 4（a）所示。

从图中可以看出，STEP 的性能优于 STEP（不含 GSL），这表明我们的图结构学习模块始终发挥着积极作用。同时，无 GSL 的 STEP 仍然取得了令人满意的成绩，这表明段级表示法发挥了重要作用。STEP 的表现也优于 STEP w/o reg，这表明 TSFormer 的长序列表示在提高图质量方面更胜一筹。此外，如第 1 节所述，DCRNN 代表了一大类基于 seq2seq [32] 架构的 STGNN [21, 26, 29, 41]。我们根据公式（5）将 TSFormer 的表示融合到 seq2seq 编码器的潜在表示中。我们可以看到，STEP 显著提高了 DCRNN 的性能，这验证了 STEP 的通用性。

4.5 超参数研究

我们通过实验分析了图结构学习中两个超参数的影响：掩码比率𝑟和𝑘NN图的𝑘NN。我们展示了 METR-LA 数据集的结果。

图 4(b) 和图 4(c) 分别显示了 𝑟 和 𝑘 的效果。我们发现𝑟 和𝑘 都存在最佳值。对于掩码比 𝑟，当 𝑟 较小时，时间序列中的掩码值可以通过简单的平均或插值来预测。因此，这会产生琐碎的自监督学习任务，无法获得有用的表征。当 𝑟 较大时，模型会丢失过多信息，无法学习时间模式。对于图结构学习中𝑘NN 图的𝑘来说，𝑘的值过小会使学习到的图不完整，丢失依赖信息，因此性能较差。如果𝑘的值过大，则会引入冗余，影响图神经网络的信息聚合，导致性能不理想。

5 相关工作

5.1 时空图神经网络

人工智能[37]，尤其是深度学习技术在很大程度上提高了多变量时间序列预测的准确性。在这些技术中，时空图神经网络（STGNNs）是最有前途的方法，它结合了图神经网络（GNNs）[7, 18]和序列模型[6, 32]，对空间和时间依赖性进行联合建模。GraphWaveNet [36]、MTGNN [35]、STGCN [38] 和 StemGNN [4] 结合了图卷积网络和门控时序卷积网络及其变体。这些方法基于卷积运算，有利于并行计算。DCRNN [20]、ST-MetaNet [26]、AGCRN [2] 和 TGCN [40] 结合了扩散卷积网络和递归神经网络 [6, 32] 及其变体。它们遵循 seq2seq [32] 架构逐步进行预测。此外，注意力机制在 GMAN [41] 和 ASTGCN [11] 等许多方法中得到了广泛应用。虽然 STGNN 取得了重大进展，但 STGNN 的复杂性很高，因为它需要处理每一步的时间和空间依赖性。因此，STGNN 只能将短期历史时间序列作为输入，如过去 1 小时（在许多数据集中为 12 个时间步长）。最近，越来越多的工作[10, 17, 29]侧重于图结构和图神经网络的联合学习，以模拟节点之间的依赖关系。LDS [10] 将边缘建模为随机变量，其参数在双层学习框架中被视为超参数。随机变量参数化了邻接矩阵 A 的元素伯努利分布。GTS [29] 引入了邻接图作为正则化，以提高图的质量，并将问题重新表述为单级优化问题。值得注意的是，我们沿用了 GTS 的框架，但通过预训练模型对其进行了改进，因为 TSFormer 为计算时间序列的相关性提供了更好的潜在表示。

5.2 预训练模型

预训练模型用于从海量无标记数据中学习良好的表征，然后将这些表征用于其他下游任务。最近的研究表明，在预训练模型提取的表征的帮助下，许多自然语言处理任务的性能都有显著提高 [28]。突出的例子有 BERT [8] 和 GPT [3]，它们分别基于 Transformer 编码器和解码器。Transformer 架构比 LSTM 架构更强大、更高效 [27, 32]，已成为设计预训练模型的主流方法。最近，针对图像的 Transformer 因其强大的性能吸引了越来越多的关注。ViT [9] 提出将图像分割成补丁，并将这些补丁的线性嵌入序列作为 Transformer 的输入，显示出令人印象深刻的性能。然而，ViT 需要监督训练，这就需要大量的标注数据。相反，MAE [13] 采用基于掩码自动编码策略的自监督学习。MAE 使我们能够高效地训练大型模型，其效果优于监督预训练。虽然预训练模型在自然语言处理和计算机视觉领域取得了重大进展，但在时间序列领域的进展却落后于它们。本文提出了一种基于 Transformer 块的时间序列预训练模型（命名为 TSFormer），并提高了下游预测任务的性能。

6 总结

本文针对 STGNN 无法学习长期信息的问题，提出了一种新颖的 STEP 框架，用于多变量时间序列预测。可扩展的时间序列预训练模型 TSFormer 增强了下游 STGNN。TSFormer 能够从非常长期的历史时间序列中有效地学习时间模式，并生成分段级表示，为 STGNN 的短期输入提供丰富的上下文信息，并促进时间序列之间依赖关系的建模。在三个真实世界数据集上进行的广泛实验显示了 STEP 框架和所提出的 TSFormer 的优越性。

 

现在是16:55，看完了，附录也看了，感觉这篇对我的论文的思路有帮助，所以，加油吧，这学期好好做人，把以前拖延的慢慢补上来(看了一下草稿箱，有2020年7月份的博客还没写完，呜呜呜呜，拖延鬼，讨厌死了)。