城市时空预测的统一数据管理和综合性能评估 [实验、分析和基准]《Unified Data Management and Comprehensive Performance Evaluation for Urban Spatial-Temporal Prediction [Experiment, Analysis & Benchmark]》
2023年11月1日,还有两个月,2023年就要结束了,希望在结束之前我能有所收获和进步,冲呀,老咸鱼。
GitHub:https://github.com/LibCity/Bigscity-LibCity
arXiv上的论文。
这个统一的管理框架,我其实在暑假还是刚开学的时候就看过,小老板昨晚突然发给了我一篇论文,我一看,?我之前见到过。他说明天开例会讨论架构,行吧,那就仔细看看吧。
摘要
解决了访问和利用不同来源、不同格式存储的不同城市时空数据集,以及确定有效的模型结构和组件。
1.为城市时空大数据设计的统一存储格式“原子文件”,并在40个不同的数据集上验证了其有效性,简化了数据管理。
2.概述了城市时空预测模型的技术进步,指导稳健模型的发展
3.用不同的模型和数据集进行了广泛的实验,建立了绩效排行版,并确定了有前景的研究方向。
1 引言
城市时空预测在城市计算中发挥着至关重要的作用,可帮助智慧城市实现高效管理和决策。各种应用都受益于城市时空预测,包括拥堵控制 [15]、路线规划 [30]、车辆调度 [77] 和 POI 推荐 [69]。
城市时空数据与传统时间序列数据的根本区别在于,时空数据由多个空间实体的历史状态时间序列组成,这些实体之间存在相互影响。因此,时空预测问题可以表述为多变量时间序列预测问题 [6, 54],而不是单变量时间序列预测问题 [24]。有效模拟不同实体时间序列之间的空间关系是解决时空预测问题的关键。
图卷积网络(GCN)是捕捉城市时空数据中空间依赖性的热门选择。学习图结构已成为时空预测的主流方法,人们还探索了空间注意力机制,以捕捉变量之间的动态图结构。
在深度学习技术发展和大规模数据集可用性的推动下,城市时空预测领域正在经历快速发展。然而,仍有几个挑战需要解决: 首先,由于现有城市时空数据集的来源和格式各不相同,访问和利用这些数据集具有挑战性。这些数据集通常以不同的格式存储,如 NPZ、PKL、H5、CSV 等。这种异质性给用户有效利用和探索数据集造成了障碍,尤其是对该领域的新手而言。这阻碍了该领域的发展和标准化,也为有效的数据管理和利用带来了障碍。
其次,随着该领域深度学习模型的激增,确定有效的模型结构和设计变得越来越困难。深度学习模型在时空预测方面表现出了最先进的性能,导致该领域的研究论文激增。然而,随着模型变得越来越复杂和多样化,确定哪些技术是真正有效的,哪些方向具有未来研究的潜力,就变得非常具有挑战性。深度学习模型对实验参数和配置的敏感性进一步强调了探索有价值的研究方向和确定最有前途的方法的必要性。为了应对上述挑战,我们在本文中做出了以下贡献:
(1) 统一存储格式: 我们介绍了一种专为城市时空大数据设计的统一存储格式--"原子文件"。通过对 40 个不同数据集的验证,我们证明了这种格式在简化城市时空数据管理方面的有效性。这一贡献解决了以不同格式存储的各种数据集的访问和利用难题,实现了准确高效的城市预测,并增强了相关应用。
(2) 技术发展路线图: 我们全面概述了城市时空预测模型的技术进步。该路线图概述了利用深度学习对空间依赖性、时间依赖性和时空融合进行有效建模的技术。通过提供这一路线图,我们促进了先进、稳健的城市时空预测模型的开发,使研究人员能够充分利用深度学习在这一领域的潜力。
(3) 广泛的实验和性能评估:我们使用 18 个模型和 20 个数据集进行了广泛的实验,建立了性能排行榜,并对空间-时间预测领域的前人工作进行了比较。通过这些实验,我们获得了对模型性能的宝贵见解,并确定了未来有希望的研究方向。这项评估可以帮助研究人员和从业人员做出明智的决策,推动城市时空预测的进步。
通过介绍原子文件存储格式、提供技术路线图和进行综合实验,我们为有效管理城市时空数据、指导未来研究工作和促进准确高效的城市时空预测模型的开发做出了贡献。这些贡献旨在应对该领域面临的挑战,加快城市时空预测的进展,最终提高城市生活质量。
2 统一的时空数据管理
2.1时空数据单元
本节将分析城市时空数据的基本单位。
2.1.1 基本单元。时空数据的最基本单位是地理单元。根据空间分布的差异,基本地理单元数据分为三种类型:
(1) 基于点的数据: 这类数据主要包括城市兴趣点(POI)数据、GPS 采样点、城市交通传感器、交通摄像头和其他设备数据。我们可以用(𝑔𝑒𝑜𝑖, 𝒍𝑖, 𝒑𝑖 )来表示点数据,其中𝑔𝑒𝑜𝑖 是这个点的 ID,𝒍𝑖 是点𝑖 的位置、 是该点的 ID,𝒍𝑖 是该点的位置,如经纬度信息,𝒑𝑖 是该点的属性信息,如 POI 类别。
(2) 基于线的数据: 这类数据主要是路段数据。同样,我们可以用(𝑔𝑒𝑜𝑖, 𝒍𝑖, 𝒑𝑖 )来表示基于线路的数据,其中 𝑔𝑒𝑜𝑖 是路段的 ID,𝒍𝑖 是路段的位置、 通常包括起点和终点的经纬度,𝒑𝑖 是路段 𝑖 的属性,如平均速度。
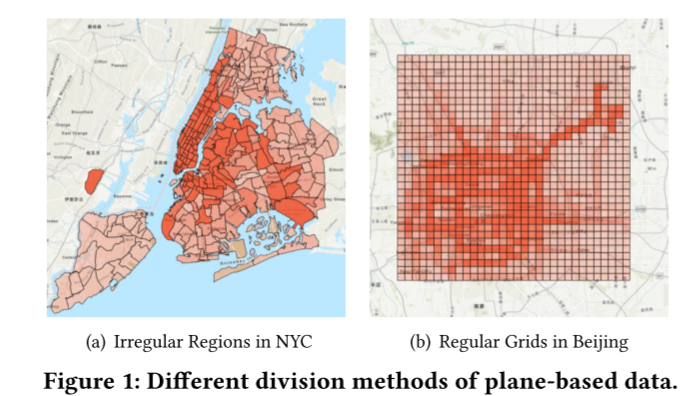
(3) 平面数据: 这类数据主要是行政区等城市区域数据。特别是通过城市区域网格划分获得的城市网格数据也属于平面数据。图 1 给出了划分城市区域的不同方法。同样,我们可以用(𝑔𝑒𝑜𝑖, 𝒍𝑖, 𝒑𝑖 )来表示基于平面的数据,其中 𝑔𝑒𝑜𝑖 是区域的 ID,𝒍𝑖 是该区域的位置、 通常包括区域边界位置的经纬度,𝒑𝑖 是区域 𝑖 的属性信息,如该区域的交通流入或流出量。
2.1.2 单位关系。单元关系数据描述了城市空间中地理单元之间的关系,如道路连通性和距离关系。鉴于这些关系呈现出不同的结构,我们通过以下方式进一步细化地理单元之间的相互联系:
(1) 图形关系数据: 图网络数据包括城市传感器图、POI 图、路网图、区域图等。一般来说,我们可以将这类图数据定义为 G = (V, E, 𝑭V, 𝑨),其中 V 是一组𝑁节点(𝑁 = |V|),E ⊆ V×V 是一组边、 𝑭V∈R𝑁×𝐷是一个𝐷维属性矩阵,𝑨∈R𝑁×𝑁是节点间的加权邻接矩阵。
(2) 网格关系数据: 常见的欧氏邻域数据是城市网格数据,可表示为 𝑭𝑽 ∈ R𝐼×𝐽×𝐷 ,其中城市被划分为 𝐼 × 𝐽 个网格,每个网格 𝑉(𝑖, 𝑗 ) 都有𝐷 个属性。每个网格都与欧几里得邻域中周围网格的分布相匹配。
(3) 图形 OD 关系数据: 这类数据主要关注出发地和目的地之间的关系,是一种粒度更细的关系数据。我们用 𝑭E∈ R𝑁×𝑁×𝐷 来表示 V 中每对节点之间的𝐷维 OD 数据(或者说每条边的𝐷维数据),其中每个条目 𝑭 (𝑖, 𝑗 ) E∈ R𝐷 代表𝑁维数据。表示从节点 𝑣𝑖 到节点 𝑗 的𝐷维属性。
(4) 网格 OD 关系数据: 具体而言,对于城市网格间的 OD 数据,可以用 𝑭E ∈ R𝐼×𝐽×𝐼×𝐽×𝐷 表示,每个条目𝑭 (𝑖1, 𝑗1 ),(𝑖2, 𝑗2 ) E 表示𝐷维属性,这些属性来自于E 表示从ᵃ𝑟𝑖𝑑(𝑖1, 𝑗1 ) 到ᵃ𝑟𝑖𝑑(𝑖2, 𝑗2 ) 的维属性。
让我们弄清楚图形关系数据和图形 OD 关系数据之间的区别。图关系数据涉及图网络 G 中图节点的属性,即 𝑭V ∈ R𝑁×𝐷,如每个节点的流量速度、 𝑭E ∈ R𝑁×𝑁×𝐷 ,表示从边的起点到终点的传输流。这通常用于模拟交通网络中起点-终点对之间的交通流。同样,对于网格关系数据,我们可以将其细化为每对网格之间的 OD 数据,其中边的属性代表网格之间的交通流。
2.1.3 单位动态。时空动态数据是指城市地理单元随时间变化的属性信息。通过在单元关系数据中加入时间维度的动态属性,我们可以获得复杂的时空数据。这类数据的例子包括城市交通流量、交通速度和乘客需求,它们都表现出动态的时空特征。为了说明这一点,让我们考虑一下图关系数据。当图形属性𝑭V ∈ R𝑁×𝐷 随时间变化时,我们可以用一个时空张量来表示𝑁节点在𝑇时间片上的𝑁维时空属性,记为𝑿 ∈ R𝑇×𝑁×𝐷 。为了全面了解不同的数据类型,请参考表 1,探索单元关系和单元动态之间的直观关系。
2.1.4 外部信息。外部数据是指提供与时空动态相关的额外背景的环境信息。这些数据源提供的辅助信息可以提高城市时空预测的准确性。外部数据的例子包括城市交通事故、重大事件和日历数据,其中包括一周中的哪一天、一天中的什么时间以及是否有节假日等因素。通过整合这些外部数据源,我们可以利用它们的宝贵见解来提高时空预测的精度。
2.2 原子文件
现有的开放源码时空数据集通常以各种格式存储。这种情况不可避免地给希望使用这些数据集的用户带来了挑战和负担。为了解决这个问题,我们在上一节讨论的时空数据单元、关系和动态分析的基础上,提出了 "原子文件 "的概念作为解决方案,为城市时空数据提供统一的存储和管理格式。这些原子文件代表了城市时空数据的最小信息单元。它们可分为四种类型: 地理单元数据、单元关系数据、时空动态数据和外部数据(可选)。
我们采用类似 CSV 文件的逗号分隔值格式来存储这四类原子文件。每个原子文件由多列数据组成。为了区分不同类型的原子文件,我们指定了特定的文件后缀。此外,我们还对原子文件每一行所包含的信息制定了具体的指导原则,如表 2 所示。精确定义如下 :
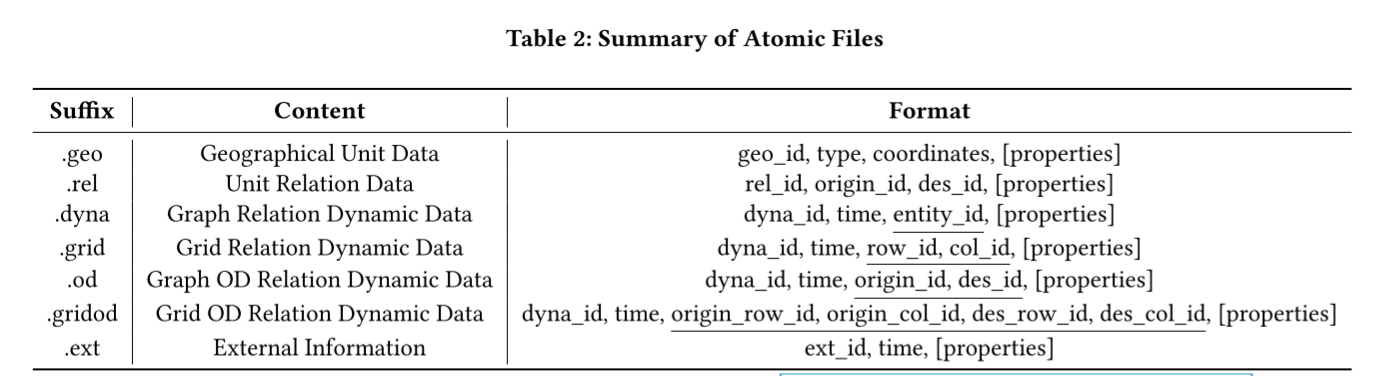
(1) ".geo "表存储地理单元数据,要求包括 geo_id(主键)、地理单元类型(点、线或多边形)和坐标信息(如经度和纬度)。其他附加属性应存储在上述三列之后,如兴趣点(POIs)类别或路段长度。
(2)".rel "表存储单位关系数据,应由 rel_id(主键)、origin_id 和 des_id 组成。origin_id 和 des_id 分别代表关系中起点实体和终点实体的 ID。这些 ID 源自".geo "表中的 geo_id 列(外键)。还可以选择包含其他属性来表示关系的权重。.rel "表中的每一行代表一条从起点到终点的有向边。
(3) 时空动态数据存储在".dyna "表中、 ".grid"、".od "和".gridod "表中,由于单元关系不同,这些表又分为四个子文件。这些表中的每一行都代表在特定时间收集到的地理实体(或实体关系)的属性。例如,dyna 表存储与图形关系数据相关的时空动态数据。它必须包括 dyna_id(主键)、时间、实体_id 和至少一个属性,如空气质量和交通流量。时间列表示数据收集的时间戳,实体_id 列表示数据收集的来源。这四类表的主要区别在于实体_id 列。在 dyna 表中,entity_id 源自 geo_id。在网格表中,为简单起见,实体_id 从网格中与地理坐标对应的行和列 ID 派生。在".od "表中,entity_id 代表 OD 关系实体的 origin_id 和 des_id。最后,在".gridod "表中,entity_id 对应于网格 OD 关系实体的行和列 ID。
(4) ".ext "表存储外部数据,必须包含 ext_id(主键)、时间和至少一个属性。
为便于理解,我们以图 2 中的洛杉矶交通速度数据集为例进行说明。该数据集由三个原子文件组成:geo、rel 和 dyna,因为它不包含任何相应的外部数据。值得注意的是,".rel "表中的 origin_id 列、des_id 列和".dyna "表中的 entity_id 列均源自".geo "表中的 geo_id 列。具体来说,".geo "表包含 207 个道路传感器的位置。.rel "表存储这些传感器之间的距离关系,通常用于构建图结构。最后,".dyna "表记录了这些传感器在 2012 年 3 月至 6 月期间以 5 分钟为间隔收集的平均交通速度信息。

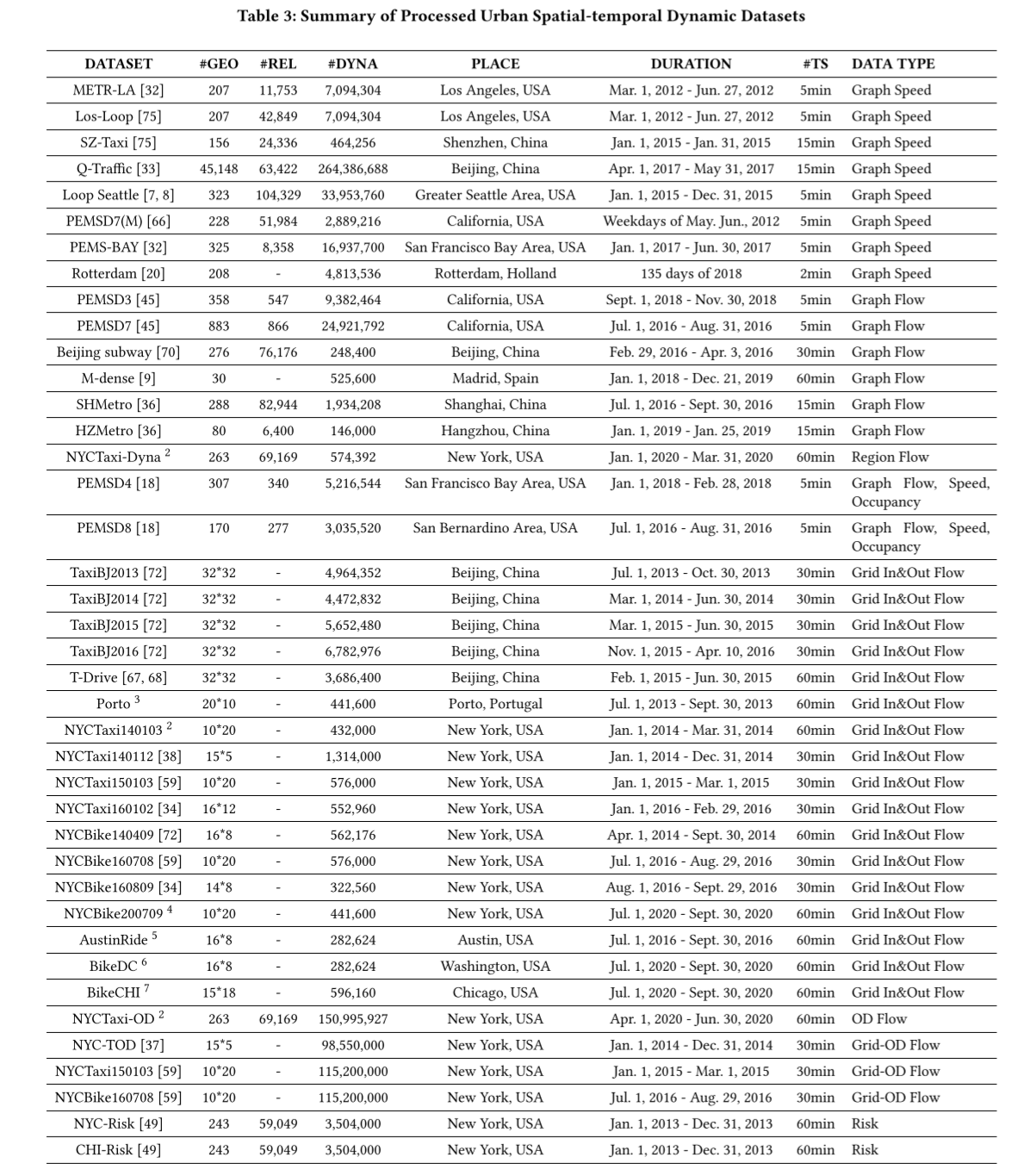
为了验证原子文件格式的有效性,我们收集了来自 17 个城市的 40 个时空动态数据集,并将其转换为原子文件格式,如表 3 所示。处理后的数据集以及相关的数据转换脚本可在 GitHub 1 上获取。我们坚信,采用统一的数据存储格式可以大大缓解与管理城市时空数据相关的挑战。这种标准化将使更多人能够利用城市时空数据,推动城市时空数据领域的快速发展。
(Sorry,看睡着了,继续。)
3 问题表述
略。
4 时空预测模型路线图
4.1 空间依赖性
根据地理学第一定律,"任何事物都与其他事物有关,但相互接近的事物关系更为密切",城市时空数据中存在空间依赖性。此外,由于城市结构区和功能区的划分,城市时空数据具有空间层次性。因此,由于功能的相似性,即使距离较远的地点也可能表现出很强的空间依赖性。数据的空间依赖性是时空预测任务与时间序列预测任务的核心区别。
(1) 卷积神经网络(CNN): CNN 被广泛用于网格关系数据建模,因为这些数据是欧氏数据。研究人员通常根据经纬度将城市划分为网格,这样就可以将时空属性数据视为图像。这样,CNN 就能从不同的网格中提取空间依赖关系 [34, 38, 50, 60]。例如,ST-ResNet [72] 利用深度残差 CNN 网络进行交通流量预测。
(2) 图神经网络(GNN): GNN 具有很强的图表示能力,因此被广泛用于图关系数据建模 [2-4、6、11、14、22、23、26、27、32、35、41、44、45、55、62、66、73-75]。在 GNN 中,图卷积神经网络(GCN)[10] 最常用于时空预测任务。图卷积模型的一个基本问题是构建图邻接矩阵,早期的研究通常使用静态邻接矩阵[32, 66]。然而,预定义的图邻接矩阵可能无法准确反映时空数据中的实际空间依赖关系。为了解决这个问题,有人提出了自适应图形生成模块 [2,56]。此外,一些研究侧重于学习动态空间依赖关系,以模拟数据随时间变化而产生的影响 [19、22、73]。为了模拟连续的空间依赖关系,基于图形 ODE 的模型被用于时空预测[13]。
(3) 空间注意机制: 空间注意力机制在地理实体间时变空间依赖关系建模中起着至关重要的作用[18, 19, 29, 38, 39, 57, 58, 64, 71, 76]。通过空间注意力,模型可以在不同的时间步骤为不同的位置分配自适应权重,从而自主学习时空数据中蕴含的动态空间依赖关系。例如,GMAN[76] 提出了空间和时间注意力机制,并设计了一种门控融合技术来融合空间和时间信息。ASTGNN[19]引入了一个动态图卷积模块和自注意机制,以捕捉动态图中的空间依赖关系。
4.2 时间依赖性
城市时空数据显示出时间依赖性,类似于时间序列数据,表现出紧密性、周期性和趋势等特征。例如,上午 8 点的交通拥堵会影响上午 9 点的交通状况,而在 24 小时周期的连续工作日中,高峰时段往往出现在相似的时间。此外,节假日和工作日也会对城市时空数据模式产生明显影响。
(1) 循环神经网络(RNN): RNNs 是一种专门用于处理连续数据的神经网络,因此非常适合捕捉时空数据中的时间依赖关系[2, 7, 14, 32, 38, 58, 60, 62, 75]。为了解决 RNN 无法模拟长期依赖关系的问题,我们引入了 LSTM [25] 和 GRU [5],作为原始 RNN 模型的变体。这些模型结合了一种门控机制,使它们能够捕捉长期依赖关系。Seq2Seq 模型[46]是一个流行的框架,它将 RNN 同时用作编码器和解码器,以实现多步时空预测。
(2) 时序卷积网络(TCN): TCNs旨在以并行方式处理顺序数据,而递归神经网络(RNN)由于依赖历史信息,不可能做到这一点。TCNs 本质上是用于时间序列预测领域的一维 CNN 模型。它们只考虑给定时间步之前的信息,被称为因果卷积。为了增加感受野,在因果卷积中使用了扩张卷积。多层扩张因果卷积(也称为 WaveNet [48])可以堆叠在一起,以实现感受野的指数增长。TCNs / 1D-CNN 已成为时空预测领域的常用基础设施[16-18, 39, 55, 56, 66]。
(3) 时间注意机制: 时间注意力机制通过在不同的时间步长为数据分配不同的权重,实现对时空数据中非线性时间依赖关系的自适应学习[1, 16, 18, 29, 34, 39, 57, 76]。这种机制有助于解决 RNN 模型在模拟长期依赖关系方面的局限性,尤其是在与 Seq2Seq 模型相结合时。最近,基于自我注意的 Transformer 模型在时间序列预测方面取得了可喜的成果,并被应用于城市时空预测。例如,PDFormer [29] 在城市交通流量预测中引入了时空自注意机制,并结合了交通状态传播的时间延迟特性。
4.3 时空依赖关系融合
为了捕捉数据中的时空依赖关系,通常将空间模型和时间模型组合成一个混合模型,如 CNN+RNN、GCN+RNN、GCN+TCN 等。以下是一些常用的时空模型融合方法:
(1) 序列结构: 序列结构将空间和时间神经网络以并行或串行配置的方式结合起来,形成一个时空块[7, 18, 43, 55- 57, 66, 75, 76]。例如,STGCN [66] 利用 2 个 TCN 和 1 个 GCN 创建一个时空块,并将它们串行堆叠起来,以捕捉数据中的时空依赖关系。TGCN [75] 采用一种递归方法,将 GCN 和 GRU 结合起来,在每个时间步通过 GCN 后,用 GRU 递归处理输入数据。PDFormer [29] 采用多个空间自注意头和时间自注意头来学习数据中的时空依赖关系。
(2) 耦合结构: 耦合结构将空间神经网络整合到时间神经网络的计算中,最常见的方法是将 GCN 与 RNN 结合起来 [2, 3, 32, 62]。在这种方法中,RNNs(包括 GRU 和 LSTM 模型等变体)计算中的全连接操作被 GCN 操作所取代。这样,模型就能将空间依赖关系纳入时间依赖关系的学习中。这种方法的一些例子包括 DCRNN [32]、CCRNN [62]、MRABGCN [3] 和 AGCRN [2],等等。
(3) 时空同步学习: 以往对数据时空依赖性建模的研究通常使用单独的组件来独立学习空间和时间依赖性。然而,时空同步学习方法可以同时直接捕捉数据中的局部时空依赖关系。为此,需要跨时间步构建空间-时间局部图结构,并使用 GCN 学习空间-时间依赖关系。STSGCN [45] 和 STFGCN [31] 就是这种方法的两个例子。
5 实验
5.1 数据集
5.2 模型
5.3 实验设置
5.4 性能比较
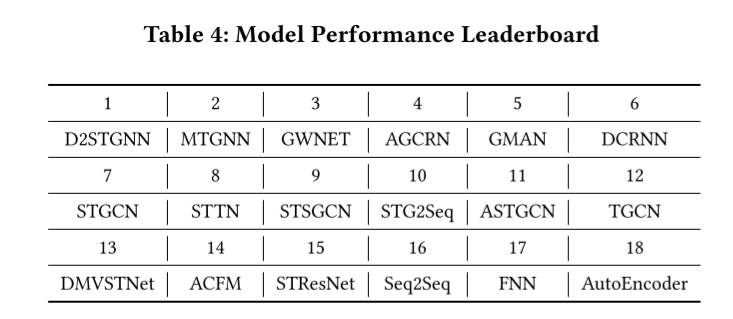
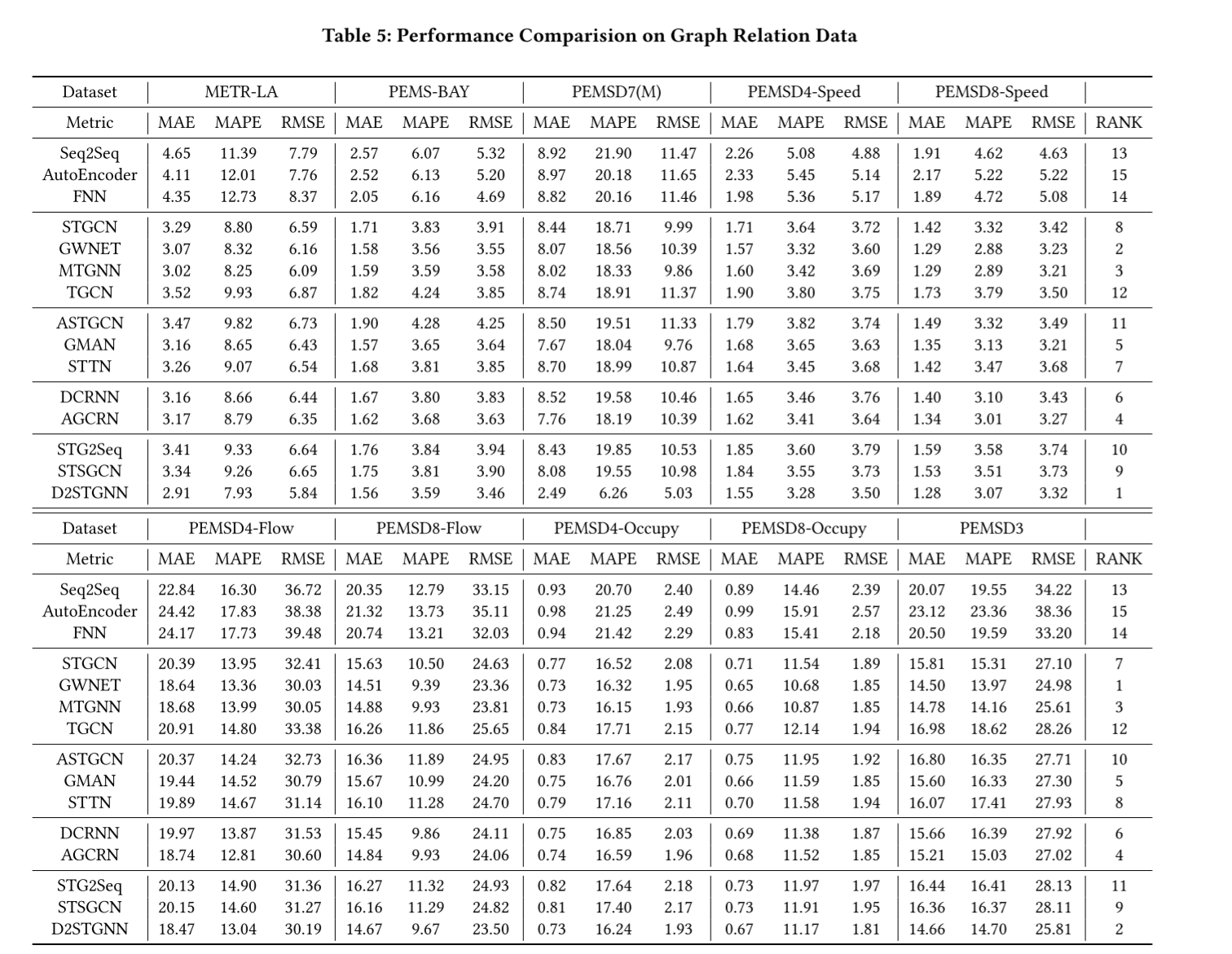
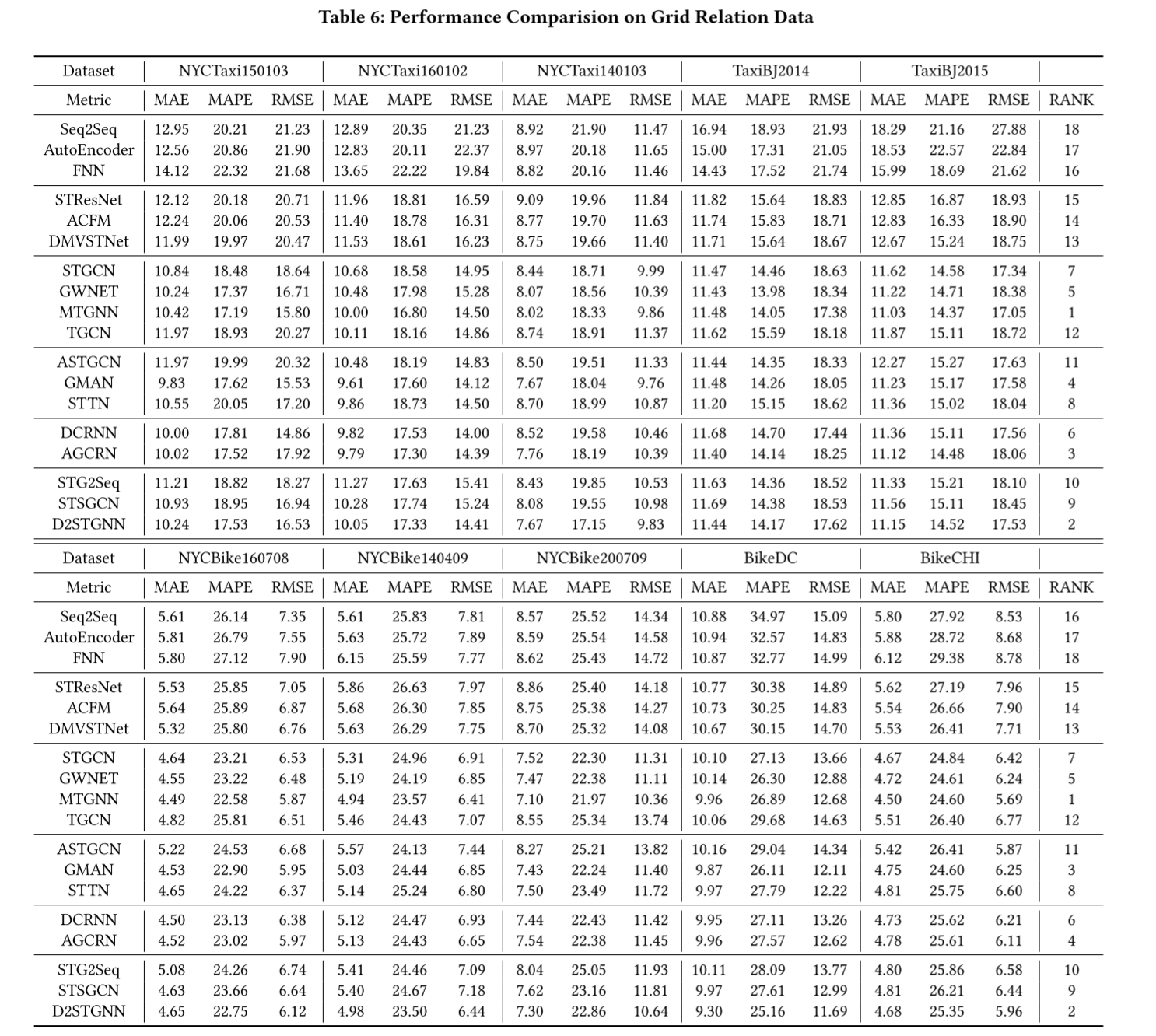
表 4 是所有模型在所有数据集上的性能排行榜。表 5 和表 6 分别列出了图形关系数据和网格关系数据的实验结果。从这些结果中,我们得出以下结论:
(1) 由于忽略了空间相关性,包括 Seq2Seq、AutoEncoder 和 FNN 在内的一般时间序列预测模型在城市时空数据上表现不佳。这表明,纳入空间相关性对提高预测精度至关重要。
(2) 基于空间-CNN 的序列结构模型,如 STResNet、ACFM 和 DMVSTNet,只适用于网格关系数据,因为 CNN 无法处理图形关系数据。虽然这些模型是为网格数据设计的,但它们的性能却比基于空间-GCN 的模型差。其中一个可能的原因是,这些模型的原始版本需要输入更遥远的历史数据信息,如一天前或一周前同一时段的数据。不过,在我们的实验中,我们删除了这些信息,以确保模型之间的公平比较。另一个原因可能是,如果构建了适当的图结构,图神经网络有能力从网格数据中捕捉空间相关性。这一优势可能有助于提高基于空间图神经网络的模型的性能。
(3) 在分析了所有表格的结果后,我们得出结论:D2STGNN 是表现最好的模型。D2STGNN 之所以能脱颖而出,是因为它利用了时空同步学习,并根据时空扩散信号和固有信号的独特性,系统地设计了扩散模块和固有模块。具体而言,每个时空信号都由扩散信号和固有信号组成,前者捕捉从其他传感器扩散的信息,后者捕捉独立于其他传感器的信息。D2STGNN 采用了一种残差分解机制,可有效分离时空信号。这样就能对时空数据的不同部分进行更精确的建模,从而提高预测精度。
(4) 接下来,MTGNN 和 GWNET 分别排名第二和第三。MTGNN 和 GWNET 这两个模型都属于将图卷积网络(GCN)与多层稀疏随性卷积(也称为 WaveNet)相结合的序列结构模型。它们还在图卷积组件中加入了自适应图结构学习模块,以解决 DCRNN 和 STGCN 中使用的固定图结构的局限性。此外,这些模型采用直接预测而非递归方法,这有助于减轻累积误差问题。MTGNN 和 GWNET 在不同的数据集上始终表现出强劲的性能。这凸显了将 GCN 与 WaveNetS 结合起来的潜力,是未来宏观时空预测领域一个很有前途的研究方向。最近的一些研究也采用了类似的结构,进一步加强了其有效性[22, 61]。
(5) 之后,排名第四的模型是 AGCRN。AGCRN 和 DCRNN 都采用了图卷积网络(GCN)与循环神经网络(RNN)相结合的耦合结构。AGCRN 引入了可学习的图结构,并采用直接预测而非递归预测,因此性能优于 DCRNN。另一方面,采用 GCN 和 RNN 相结合的顺序结构的模型(如 TGCN)性能略低。这表明,与顺序结构相比,耦合结构更适合集成 GCN 和 RNN。值得注意的是,综合排名前 4 位的模型都采用了直接预测法。直接预测方法是在学习到的隐藏状态上使用两个全连接层,直接进行多步预测,而不依赖于前几步的结果进行递归预测。这种方法有助于缓解累积误差问题,更适合城市时空预测等短期预测场景。
(6) 作为一种将空间注意力与其他成分相结合的序列结构模型,GMAN 总体排名第五。GMAN 利用时空注意力机制来学习数据中的时空相关性,因此性能良好。不过,该模型的复杂度较高,且消耗大量内存。另外两个基于注意力的模型,即 STTN 和 ASTGCN,性能比 GMAN 差,这可能是由于计算注意力的方式不同造成的。GMAN 采用了完全基于注意力机制的结构,并引入了多头注意力和群体注意力,而 STTN 和 ASTGCN 对注意力的实现较为简单。基于注意力的模型的主要局限是时间复杂度高。未来的研究可以侧重于降低模型的复杂性,并在性能和效率之间取得平衡。
(7) 最后,值得注意的是,其他采用时空同步学习的模型,如 STG2Seq 和 STSGCN,表现出略低的性能。这可能是由于它们只关注短程时空相关性,而忽略了长程相关性。另一方面,MTGNN 和 GWNET 等模型利用多层 WaveNet 架构,旨在捕捉长程时间相关性。此外,最近的研究也强调了长程空间依赖性在时空预测中的重要性[28, 29]。这些研究结果进一步强调了在空间-时间建模和预测任务中同时考虑短程和长程相关性的重要性。
5.5 模型效率研究
表 7 分别显示了图形关系数据和网格关系数据每个 epoch 的训练和推理时间。由于篇幅有限,这里只提供了 12 个数据集的结果。不过,值得注意的是,其他数据集的效率表现通常与表 7 所示数据集类似,如 PEMSD4-Flow、PEMSD4-Occupy 和 PEMSD4-Speed。在整个实验过程中,我们使用了一致的批量大小 16,以防止 GPU 内存消耗超过单卡容量。基于这些结果,我们可以得出以下结论:
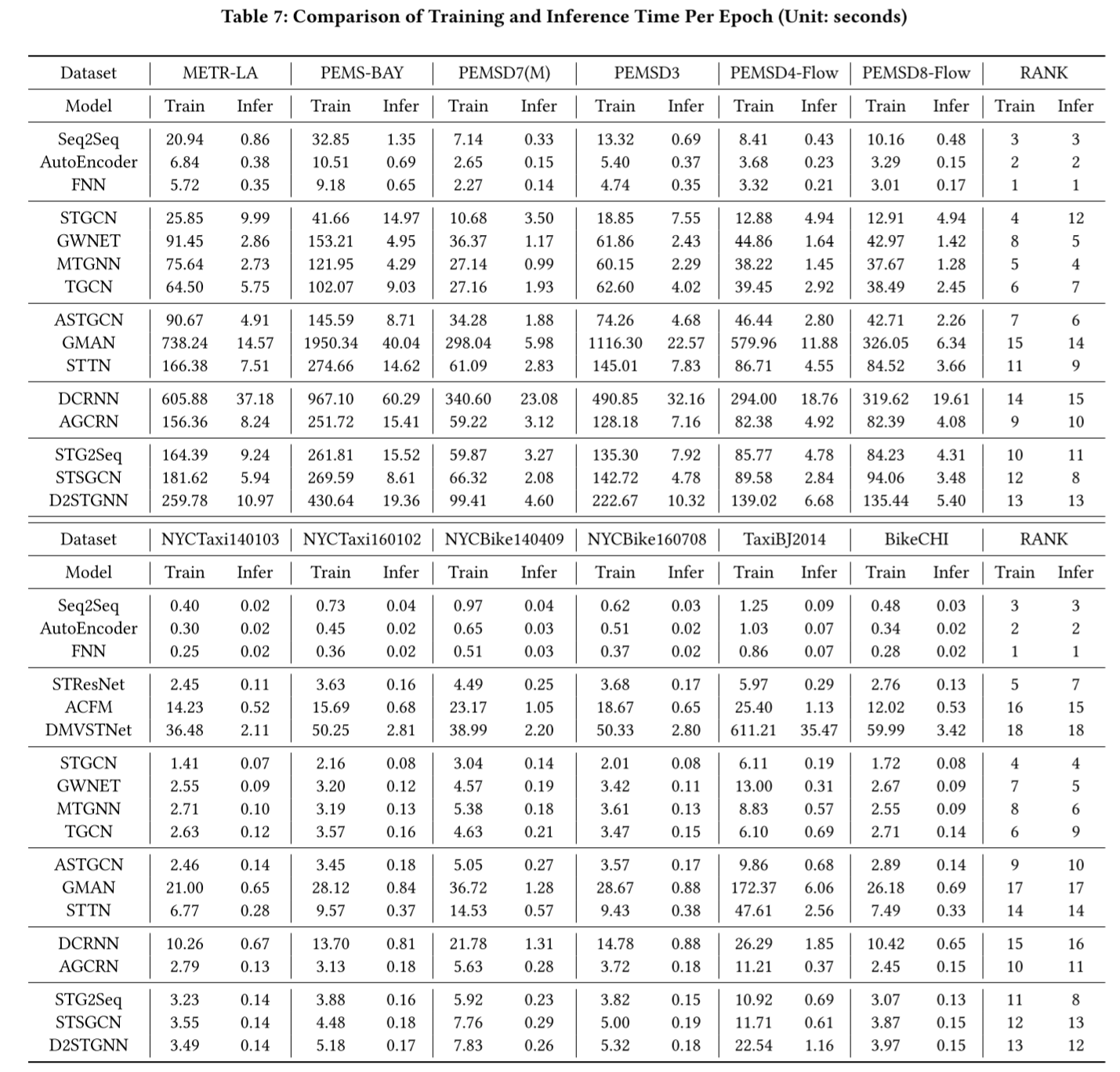
(1) 不考虑空间实体之间空间依赖关系的一般时间序列预测模型的训练和推理时间明显快于其他模型。
(2) 在三种基于空间网络的序列结构模型中,STResNet 以其相对较高的计算效率脱颖而出。这主要归功于它使用了基于卷积的残差网络,与 ACFM 和 DMVSTNet 等包含 RNN 和注意力机制的模型相比,其计算效率较高。
(3) 在其他序列结构模型方面,与 GMAN 和 STTN 等基于空间注意力的模型相比,STGCN、GWNET、MTGNN 和 TGCN 等基于空间 GCN 的模型表现出更高的计算效率,尤其是在处理 TaxiBJ2014(1024 个节点)等大型图时。这主要是因为基于空间注意力的模型需要计算每个空间实体与所有其他空间实体之间的注意力,导致计算成本较高。相比之下,基于空间GCN 的模型通常只关注每个空间实体在特定距离或跳数范围内相邻空间实体的空间依赖关系。因此,它们的计算成本要低得多。这些基于空间注意力的模型优先考虑性能而非计算效率。虽然它们的计算效率可能较低,但它们的目标是提供卓越的模型性能。
(4) 与 DCRNN 和 AGCRNN 等耦合结构模型相比,STGCN、GWNET 和 MTGNN 等顺序结构模型的训练和推理时间一般较短。这主要是由于在序列模型中使用了时序卷积网络(TCN),与耦合结构模型中使用的循环神经网络(RNN)相比,TCN 的计算速度通常更快。
(5) 在进行多步预测时,与 GWNET、MTGNN、TGCN 和 ASTGCN 等直接预测模型相比,DCRNN 和 GMAN 等递归预测模型的训练和推理时间要长得多。递归预测模型通常采用编码器-解码器架构,并根据之前的预测结果生成预测结果,因此不适合并行计算,从而增加了计算复杂度。然而,直接预测模型可以一次性预测多个步骤的结果,从而加快了训练和推理时间。
(6) STG2Seq、STSGCN 和 D2STGNN 等时空同步建模模型的效率相对较低,这可以归因于其中包含了较为复杂的时空联合学习模块。只有一些大型模型的效率低于它们,如 DCRNN 和 GMAN,但这两种模型主要受限于循环预测范式。虽然 D2STGNN 是性能最高的模型,但其效率与排名第二和第三的MTGNN 和 GWNET 相差甚远。在为特定应用选择模型时,关键是要考虑应用场景的要求,同时兼顾效率和性能,从而做出适当的决定。
5.6 预测结果和性能差异分析
我们根据表 4 从每个类别中选出性能最好的模型,并在图 3(1) 和图 3(2) 中分别显示了它们对不同时间和不同日期的 METR-LA 和 PEMSD8-Speed 数据集的预测结果。对于每个数据集,我们绘制了四个子图:(a)和(b)分别显示了一天中不同时间和一周中不同日期的平均车速趋势;(c)和(d)分别显示了工作日和周末不同时间模型预测值与地面实况之间的平均绝对百分比误差(MAPE)。
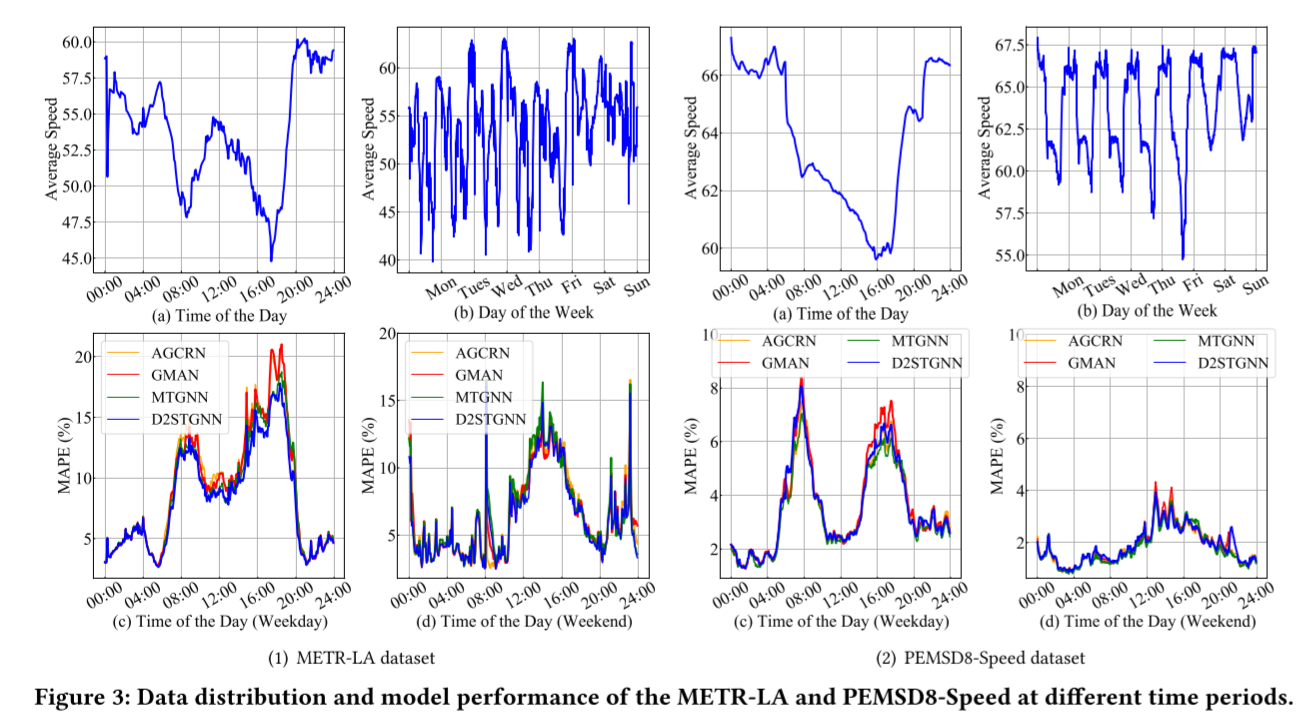
从子图 (a) 和 (b) 中,我们可以观察到真实数据中的高峰期和周期性。高峰期通常集中在 8:00 和 17:00 左右,而数据在工作日和周末分别呈现周期性模式。此外,与工作日相比,周末的车速分布更为集中,方差更小。相应地,根据(c)和(d)分图,模型在工作日和周末的表现有显著差异。模型在周末的表现更好,这可能是因为周末的数据分布更集中。然而,在工作日,所选模型在非高峰期的性能相对接近,而在高峰期则存在明显的性能差距。造成这四种模型之间性能差距的主要原因是它们在高峰期的性能。
如图(a)和(b)所示,高峰期的交通状况往往变化更复杂、更迅速,更有可能出现交通拥堵或交通事故等极端情况。因此,预测高峰期的交通状况比预测其他时段的交通状况更具挑战性。然而,在实际应用中,人们更关心的恰恰是高峰期的准确交通预测。这些数据还表明,提高模型的整体性能有赖于提高其在高峰期的预测准确性。这些观察结果为研究人员今后设计和开发更好的交通模型提供了方向,重点是捕捉高峰期交通状况的波动。
6 结论
6.1 局限性和未来工作
必须承认本研究的局限性。本文主要关注城市时空预测领域中交通领域的交通预测,而较少关注其他相关领域,如空气质量预测、气候预测和犯罪频率预测。之所以做出这样的选择,是因为交通预测是城市时空预测中最关键、发展最快的领域之一。不过,有必要强调的是,所提出的 "原子文件 "格式并不局限于交通数据。它可以应用于各种其他类型的城市时空数据,包括温度、风速、犯罪事件等。
探索其他领域的时空预测任务(如气象学)是未来工作的一个潜在途径。扩大研究范围,涵盖更广泛的预测任务,将有助于更全面地了解城市时空动态,促进各领域的技术进步。未来的工作将包括探索更多的时空预测领域,扩大这项工作的实用性,并进一步加强我们对不同背景下时空动态的理解。
6.2 结论
总之,这项工作解决了城市时空预测领域面临的挑战,为数据管理和预测技术做出了重要贡献。通过引入统一的存储格式 "原子文件",我们简化了对多样化城市时空数据集的访问和利用,提高了数据管理效率。对预测模型技术进展的全面概述为研究人员开发稳健的模型提供了宝贵的见解和指导。此外,利用各种模型和数据集进行的大量实验建立了性能基准,并确定了有前途的研究方向。
展望未来,本研究成果和方法为城市时空预测的未来研究铺平了道路。研究人员和从业人员可以利用统一的存储格式、技术路线图和模型性能基准来探索新途径、开发创新模型,并为该领域的进步做出贡献。最终,这些努力将带来更有效的城市时空数据管理、更强的预测能力以及更好的城市规划和发展。
现在是20:24,搞完了( ̄ェ ̄;)。





