狼抓兔子——平面图转对偶图

 P4001 [BJOI2006]狼抓兔子

题目描述

现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到，但抓兔子还是比较在行的，而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：

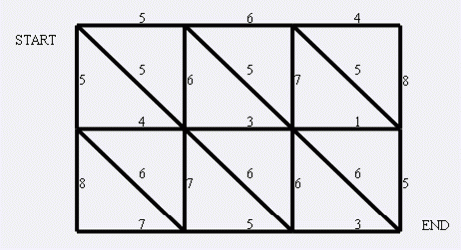
左上角点为(1,1),右下角点为(N,M)(上图中N=3,M=4).有以下三种类型的道路

1:(x,y)<==>(x+1,y)

2:(x,y)<==>(x,y+1)

3:(x,y)<==>(x+1,y+1)

道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的. 左上角和右下角为兔子的两个窝，开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下角(N,M)的窝中去，狼王开始伏击这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为K，狼王需要安排同样数量的K只狼，才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦。

输入输出格式

输入格式：

 

第一行为N,M.表示网格的大小，N,M均小于等于1000.

接下来分三部分

第一部分共N行，每行M-1个数，表示横向道路的权值.

第二部分共N-1行，每行M个数，表示纵向道路的权值.

第三部分共N-1行，每行M-1个数，表示斜向道路的权值.

 

输出格式：

 

输出一个整数，表示参与伏击的狼的最小数量.

 

输入输出样例

输入样例#1： 

3 4
5 6 4
4 3 1
7 5 3
5 6 7 8
8 7 6 5
5 5 5
6 6 6

输出样例#1： 

14
做这个题，第一反应肯定是网络流求最小割，但是一看数据范围就会发现，网络流会爆炸的，所以我们就通过对偶图把问题转换为求最短路
下面是代码（%%%dzy)

// luogu-judger-enable-o2
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define maxn 2000010
#define INF 1000000000
using namespace std;

int n, m, a[1010][1010], b[1010][1010], c[1010][1010], id[1010][1010][2], s, t, cnt;

inline int read(){
    int x = 0; char c = getchar();
    while(c < '0' || c > '9') c = getchar();
    while(c >= '0' && c <= '9'){x = x * 10 + c - '0'; c = getchar();}
    return x;
}
//10^5以上要用快读，不然会炸 
struct Edge{
    int to, next, w;
}e[3 * maxn]; int sz, head[maxn];
inline void add_edge(int u, int v, int w){
    e[sz].to = v; e[sz].w = w;
    e[sz].next = head[u]; head[u] = sz++;
    e[sz].to = u; e[sz].w = w;
    e[sz].next = head[v]; head[v] = sz++;
}//因为是无向图，所以同时存两条边 

int dis[maxn];
deque<int> Q; bool vis[maxn];
void spfa(){
    memset(dis, 10, sizeof dis); vis[s] = 1; Q.push_back(s); dis[s] = 0;
    while(!Q.empty()){
        int u = Q.front(); Q.pop_front(); vis[u] = 0;
        for(int i = head[u]; ~i; i = e[i].next){
            int v = e[i].to, w = e[i].w;
            if(dis[v] > dis[u] + w){
                dis[v] = dis[u] + w;
                if(vis[v]) continue; vis[v] = 1;
                if(Q.empty() || dis[v] <= dis[Q.front()]) Q.push_front(v);
                else Q.push_back(v);
            }
        }
    }
    cout << dis[t];
}

int main(){ memset(head, -1, sizeof head);
    n = read(); m = read(); s = 2 * (n - 1) * (m - 1) + 1, t = s + 1;
    if(n == 1 || m == 1){
        if(n < m) swap(n, m); 
        int ans = INF;
        for(int i = 1; i < n; ++i) 
        ans = min(ans, read()); 
        cout << ans; return 0;
        //如果只有一行的话，我特判一下输出最小值即可 
    }
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j < m; ++j)
            a[i][j] = read();
    for(int i = 1; i < n; ++i)
        for(int j = 1; j <= m; ++j)
            b[i][j] = read();
    for(int i = 1; i < n; ++i)
        for(int j = 1; j < m; ++j){
            c[i][j] = read();
            id[i][j][0] = ++cnt;
            id[i][j][1] = ++cnt;
            //用id[i][j][0]表示正方形里上面的点 ，id[i][j][1]表示下面的点，每一个方格属于哪两个点要写明白 
        }
        
    //把每一个值都存起来，在连边的时候就可以离线做了
     
    for(int i = 1; i < n; ++i)
        for(int j = 1; j < m; ++j)
            add_edge(id[i][j][1], id[i][j][0], c[i][j]);
            //斜着的边可以直接连 
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j < m; ++j){
            if(i == 1) add_edge(id[i][j][0], t, a[i][j]);
            else if(i == n) add_edge(s, id[i - 1][j][1], a[i][j]);
            else add_edge(id[i][j][0], id[i - 1][j][1], a[i][j]);
        }
    //横向的边要进行特判，第一行的上点与起点相连，最后一行的下点与终点相连 
    
    for(int i = 1; i < n; ++i)
        for(int j = 1; j <= m; ++j){
            if(j == 1) add_edge(s, id[i][j][1], b[i][j]);
            else if(j == m) add_edge(id[i][j - 1][0], t, b[i][j]);
            else add_edge(id[i][j][1], id[i][j - 1][0], b[i][j]);
        }
    //竖向的边也是要特判，同理可得    
    
    spfa();
    //spfa跑最短路即可
    //最好还是用dijkstra写 ，因为稠密图用spfa跑还是非常容易炸的，但是现在bzoj和luogu都能A，所以我就不改dijkstra了 
    return 0;
}