【CSAPP笔记】2. 整型运算

现在想补补推荐这本书的理由。

Most books on systems—computer architecture, compilers, operating systems, and networking—are written as if the reader were going to design and implement such a system. We call this the “builder's persepective.” We believe that students should first learn about systems in terms of how they affect the behavior and performance of their programs—a “programmer's perspective.”

For programmers, what really matters is how the finite word sizes used to represent integer and floating point data determines what values can be represented and the behavior of different operations.

在上一篇笔记中，在浏览CSAPP课程网站时，有一段话让我印象深刻。本书的标题中有A Programmer's Perspective，那么，何为A Programmer's Perspective？作者认为，大多数的、涉及方方面面的计算机书籍，组成原理、编译器、操作系统、网络……等等，很多都是以“建设者”的角度（builder's perspective）来写成一本书的。这些书的作者认为他要面向的读者，买这本书来看的目的是真的要搭建/配置/写出来一个完整的Network/OS/complier等等。

就以信息在计算机的表示来举例，数字逻辑、数字电路等书籍会切切实实教它的读者怎么样去实现一个有效率的计算电路。这本书的特色就是：从程序员的角度出发的，程序员更想需要知道的是：机器是如何以有限的字长来表示无符号和有符号整型，以及浮点数的编码规则。

The material in this book has direct value for programmers. Students find that it explains many of the mysterious problems they've already encountered, that it helps them write and debug code more efficiently, and that their programs are more reliable and efficient.

为什么两个数加起来会变成一个负数？作为学生的我们，肯定会遇到这个问题。但是在课堂上，老师往往只会抛出两个字“溢出”。我们知道“溢出”了，但我们不知道何为“溢出”，为何“溢出”，“溢出”到底是“怎样溢出”的。知其然，还要知其所以然。这些看似神秘的问题，在这本书里都有很好的解答，会让你有豁然开朗之感。理解了底层原理，能帮助你更高效的debug，写出更可靠的程序。

The material in this book is unique. Much of it is not presented in any other book or taught in previous courses. Instead, a traditional coverage of systems requires programmers to figure out on their own how the characteristics of the systems they study in builder-centric courses can be exploited to improve their programs. The book provides a solid foundation for builder-centric courses. We believe that more advanced systems courses should present systems from a builder's perspective. Students will be much better oriented to the needs and constraints of these systems by first studying them from a programmer's perspective.

都说中国计算机教材饱受诟病，当然的确也肯定有那么些真材实料，但饱受诟病的原因就是很多书都是抄外国的，再加上一点自己的东西。要么就是直接国内互相抄。有点再为了让“中国人看得懂”，翻译的就烂了，甚至添油加醋，出现错误的都有。我就特别佩服这种敢直接说“我们的材料都是独一无二”的这种精神。这本书是美国CMU（卡内基梅隆大学，Carnegie Mellon University）的一门课程——ICS，Intro to Computer Systems（计算机系统导论）的教材，本书的作者在CMU坐镇亲自授课。这门课也成为了CMU的“镇校神课”。这本“以程序员角度”来写的书，CSAPP，能够为我们以后学习以建设者思想为中心的更高级的课程打下坚实的理论基础。

2017-04-12 update：到目前为止看了这本书两个月，进度差不多是一半，觉得这本书知识点结构清晰，有逻辑有条理，叙述又准确，又有翔实的补充资料，题目也是精心编排的，PPT做的又好，还有lab可以做，确保能让读者真正的学到东西。反观大学的计算机组成原理课的教材，要条理没条理要逻辑没逻辑，填鸭式地强行灌输知识点，PPT质量惨不忍睹，例题和课后题一看就是应试。拿IEEE浮点规则来说，根本没几个同学学懂了这个编码规则，但实际上它是很beautiful的，但被垃圾教材教成了什么样子...不知道这种全方位被碾压的东西为何还存在于大学课堂上，简直是根本没道理的事情。课这么烂，还不如少上几节课。

整数运算

两数相加会得出一个负数？！

表达式 x < y 和表达式 x - y < 0 有可能产生不同的结果？！

这些其实是因为计算机运算的有限性而导致的。理解这些计算的细微之处能够让我们编写更加可靠的代码。

无符号加法

考虑两个无符号整数x和y，如果都是w位无符号数字（以下的w都代表w位无符号数），那么满足 0 ≤ x, y ≤ 2^w - 1 。如果计算x和y的和，那么得到的结果可能需要w+1位。如果出现了需要w+1位的情况，那么就是加法上溢了。

说的更明白一点，对于我们最熟悉的十进制，三位数加三位数的结果最多用四位数表示就够了（999+999=1998）此时x，y是十进制下的加数，0 ≤ x, y ≤ 10^3 - 1，结果可能需要4位。

如果说，为了不出现上溢，那我扩宽机器支持的数字位数行不行？如果为了让两个 w 位数加起来不溢出，那么我们需要 w + 1 位，因此就可以存储 w + 1 位的数。而两个 w + 1 的数相加，有需要 w + 2 个位来保证不会上溢……依次类推，这种“膨胀”意味着，如果我们想这么做的话，那么我们只能对字长不加任何限制。例如Lisp，事实上就支持无限精度运算（当然要在机器的存储器限制之内）。更常见的是，编程语言支持固定精度的运算，所以说，如果超出机器能表示的范围，那么运算结果就是溢出了。

可以把无符号加法 x + y 视为一种模运算形式，等价于加法运算后的结果模上2的w次方。可以这么理解，因为如果溢出，是相当于进位，也就是比w位多一位，那么那一位就会被抛弃。模2的w次方这个动作，就好似“丢掉”了这个第 w + 1 位的进位数字。例如一个4位数字（中括号是其二进制位表示） x = 9 [1001] 和 y = 12 [1100]，加法运算结果是21 [10101]。丢弃最高位的结果是[0101]也就是十进制5，可以把5认为是21 mod 16 = 5。

简单的说，如果现在有一台支持4位的无符号数加法运算的“计算器”摆在你面前，那么大于2^w也就是16的结果都是溢出的。

C语言程序中，不会把溢出作为错误而发送信号。考虑一个函数，判断两个无符号数相加会不会产生溢出，那么它应该是下面这个样子的：

int uadd_ok(unsigned x, unsigned y)
{
    unsigned result = x + y;
    return (s>=x);
}

补码加法

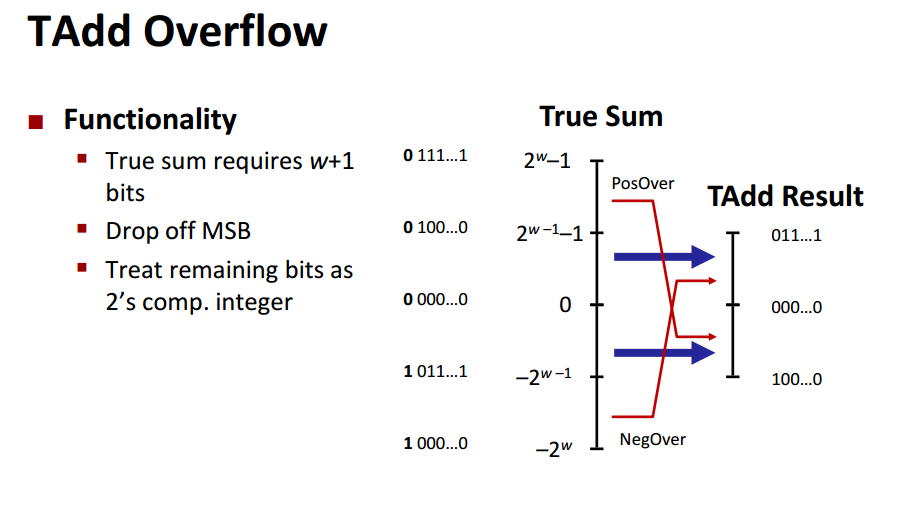
如果能够理解无符号加法的溢出，那么也就很好理解补码加法时，如果太大的结果也是会溢出的。只不过如果是正溢出的话，结果会变成一个很小很小的负数。这个现象的关键还是在于补码的编码机制。其实就正溢的情况来看，补码正溢和无符号正溢有些许不同。无符号正溢会导致现有w位放不下运算结果而溢出，而补码正溢时，是因为加法导致运算进位的1成了符号位，而符号位的权是负权。

简而言之，如果加法运算之后的结果仍然落在无符号、补码所能够表示的范围之内，那么就不会溢出，否则会溢出。溢出后结果的具体情况根据不同的编码规则来。

正溢出(positive overflow)和负溢出(negative overflow)。正溢出就是数值太大把原来为 0 的符号位修改成了 1，反而成了负数；负溢出是数值太小，把原来为 1 的符号位修改成了 0，反而成了正数。

减法、非

减法其实就是做“加一个数的相反数”，所以说还是可以归结到加法上去，然而能够顺带解决“相反数”的问题。

在初中时，相反数的定义是x + （-x） = 0，所以-x是x的相反数。对于一个无符号整数x，那么一定存在另外一个无符号整数，会让他们的相加结果为无符号0。这个结果就是2的w次方减去x。他俩的相加结果为2的w次方，需要w + 1位表示—— w + 1位是1，剩下的全为0。w + 1位会被抛弃，那么结果就是0。

补码的非有一条比较神奇的技巧。求补码的非的一种方法是——对每一位求补，在对结果加1。也可以说取反加一，也就是说如果用C语言编码，可以对任意整数值x，计算-x和~x+1两个表达式的值，他们是绝对相等的。是不是很神奇？

例如字长为4的情况，有符号整数5，那么补码表示法为[0101]，每一位取补后是[1010]，加一为[1011]，刚好是-5的补码表示法。

乘法，与移位运算的联系

两个w位的数，加起来的数可能需要w + 1位，乘起来是可能需要2w位的（具体例子像上面加法那样举一个就很明白了）。对于无符号和补码的乘法来说，乘法运算的位级表示都是一样的。但依然结果是被截断为机器最长的能够表示的位数。

这里比较有的说的是，在大多数机器上，乘法指令运算速度是比较慢的（需要10个或者更多的时钟周期）。然而其他整数运算（加减法、位运算）只需要一个时间周期。所以编译器会采取的一个重要优化就是通过位运算和加减法的组合来尝试代替乘除法运算。

我们知道“把一个数左移n位相当于乘上2的n次方”。那么，如果一个程序包含表达式 x * 14，编译器会重写为(x<<3) + (x<<2) + (x<<1) 。无论x是无符号还是补码，甚至乘法导致了溢出，直接计算x乘以14和通过位运算和加法的组合计算，两个计算都会得到同样的结果（根据运算的属性可以证明这一点）。

这是编译器会做的事情。如果我们要写 x * 14，那么就直接这么写。

除以2的幂

在大多数机器上，整数除法比乘法更慢——通常需要30个或者更多的时间周期。如果能够用右移来实现的话，那是再好不过了。不幸的是，这种方法不能推广到除以任何常数K，这点于乘法不同。乘以任何常数都可以转化成加法和左移的结合，然而不能用右移（除以2的幂）来表示除以任意常数K。

左移只有一种，就是在右边是补0。而右移有两种，就是算术右移和逻辑右移

逻辑右移，右移后在左端补0。算术右移，右移后在左端补最高有效位的值。

如果采取算术右移的话，负数除以2的幂会让左端补的是1，那么保持了负数的符号。

除法就会导致除不尽，移位会导致结果永远是向下舍入，有的时候会导致和我们的期望不一致。下面给出16位表示的-12340进行算术右移的结果。

k	算术右移k位后的位表示（相当于除以2的k次方）	结果（十进制，没有加偏移量）	实际的结果	我们期望的舍入结果
0	1100111111001100	-12340	-12340.0	-12340
1	1110011111100110	-6170	-6170.0	-6170
4	1111110011111100	-772	-771.25	-771
8	1111111111001111	-49	-48.203125	-48

我们知道，整型5除以整型2的结果是2，实质上是结果2.5“取地板”，也就是向下舍入。然而对于负数除以2的幂，我们会希望“取天花板”，也就是向上舍入。对于这个问题，我们可以在移位之前添加偏置值（biasing），通过这种方式修正不合适的舍入。对于x / y，偏移量为y - 1，也就是说有对x / y 向上舍入的结果对（x + y - 1）/y 向下舍入相同。

思考和总结

对于整数运算

正如上文提到，计算机执行整数运算实际上是一种模运算形式。表示数字的有限字长限制了数值的取值范围，所以结果可能溢出。无论是无符号、补码，在进行加减乘除移位的时候，都有完全一样或者非常类似的位级行为。

某些规定可能会产生令人意想不到的结果，而这些可能是难以察觉的bug的源头。特别地，我们看到unsigned数据类型，它们的概念很简单，但不恰当的运用它们可能导致即使是资深人士都意想不到的行为。

何时使用无符号整型呢？

如果对无符号整型的内容不是很理解，请不要使用无符号整型！

2017-04-02 update：添加一些题目。

在32位机器上运行如下代码。假设我们对有符号值使用补码运算，对有符号值使用的是算术右移，对有符号值使用的是逻辑右移。变量的初始化声明如下：

int x = ArbitraryValue();
int y = ArbitraryValue();

unsigned ux = x;
unsigned uy = y; //ux,uy 是x,y 的无符号型

对于下面的C语言表达式，请说明 1）对于所有的 x 和 y 值，表达式恒为真。或者 2）给出使表达式为假的 x 和 y 的值。

(x > 0) || (x - 1 < 0)
(x & 7) != 7 || (x << 29) < 0
(x * x) >= 0
x < 0 || -x >= 0
x > 0 || -x >= 0
x + y == ux + uy
x * ~y + ux * uy == -x

解答or提示：

若 x = TMin ，x - 1 = TMax。
7 的二进制表示是 0111 ，如果 (x & 7) != 7 这个表达式为假，那么 x 的第二位必须是 1。左移29位之后，这个1变成了符号位。
假。可能溢出
真。
TMin的逆元是TMin。当 x = TMin 时， -x 也等于 TMin。
真。补码和无符号加法有相同的位级行为。
~y = -y - 1（一个有符号数的相反数是各位取反后加一）。uy * ux 等于 x * y。因此：左边 = x * （-y - 1）+ x * y = x = 右边。

Chang Zhao

吾尝终日而思矣，不如须臾之所学也；吾尝跂而望矣，不如登高之博见也。