算法分析与设计C++ 第四章:动态规划 (附4:过河卒)
基本概念
动态规划是运筹学的一个分支,是求解决策过程(decision process)最优化的数学方法。
动态规划基本思想
动态规划算法通常用于求解具有某种最优性质的问题。
基本思想是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
步骤
- 找出最优解的性质,并刻画其结构特征
- 递归地定义最优值(写出动态规划方程);
- 以自底向上的方式计算出最优值;
- 根据计算最优值时得到的信息,构造一个最优解。
步骤1~3是动态规划算法的基本步骤。
在只需要求出最优值的情形,步骤4可以省略;
若需要求出问题的一个最优解,则必须执行步骤4。
备忘录算法
备忘录方法是动态规划算法的变形。
与动态规划算法一样,备忘录方法用一个表格保存已解决的子问题的答案,再碰到该子问题时,只要简单地查看该子问题的解答,而不必重新求解。
备忘录方法的控制结构与直接递归方法的控制结构相同,区别仅在于备忘录方法为每个解过的子问题建立了备忘录以备需要时查看,避免了相同子问题的重复求解(减少了递归调用的次数,提高运行效率)。
过河卒
总时间限制: 1000ms 内存限制: 128000kB
描述
棋盘上A点有一个过河卒,需要走到目标B点。卒行走的规则:可以向下、或者向右。同时在棋盘上的某一点有一个对方的马(如C点),该马所在的点和所有跳跃一步可达的点称为对方马的控制点,如图3-1中的C点和P1,……,P8,卒不能通过对方马的控制点。棋盘用坐标表示,A点(0,0)、B点(n, m) (n,m为不超过20的整数),同样马的位置坐标是需要给出的,C≠A且C≠B。现在要求你计算出卒从A点能够到达B点的路径的条数。
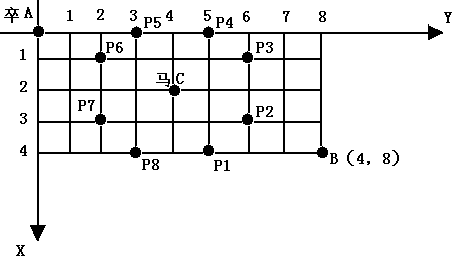
输入
B点的坐标(n,m)以及对方马的坐标(X,Y)
输出
从A点能够到达B点的路径的条数。
样例输入
6 6 3 2
样例输出
17
来源
noip普及组2002
#include<iostream>
using namespace std;
long long fun(long long n,long long m, long long x, long long y){
long long a[21][21];
int dx[9] = {0, 2, 2, 1, 1, -2, -2, -1, -1};
int dy[9] = {0, 1, -1, 2, -2, 1, -1, 2, -2};
bool g1[21][21];
fill(g1[0],g1[0]+21*21,true);
for (int i=0; i<=8; i++){
int xx=x+dx[i],yy=y+dy[i];
if (xx>=0 && xx<=n && yy>=0 && yy<=m){
g1[xx][yy]=false;
}
}
// for(int g=0; g<=n; g++)
// {
// for(int h=0; h<=m; h++)
// {
// cout<<g1[g][h]<<" ";
// }
// cout<<endl;
// }
fill(a[0],a[0]+21*21,0);
a[0][0]=1LL;
for(int g=0; g<=n; g++)
{
for(int h=0;h<=m;h++)
{
if(g1[g][h]){
if(g==0&&h>=1){
a[0][h]=a[g][h-1];
}
if(h==0&&g>=1){
a[g][0]=a[g-1][h];
}
if(g>=1&&h>=1){
a[g][h] = a[g-1][h]+a[g][h-1];
}
}
}
}
// cout<<endl;
// for(int g=0; g<=n; g++)
// {
// for(int h=0;h<=m;h++)
// {
// cout<<"("<<g<<","<<h<<"):"<<a[g][h]<<" ";
// }
// cout<<endl;
// }
return a[n][m];
}
int main(){
long long n,m,x,y;
cin>>n>>m>>x>>y;
cout<<fun(n,m,x,y)<<endl;
return 0;
}
踩坑日志
数据类型需要long long, 赋初值 需要加LL
矩阵连乘
#include<iostream>
#include<cstring>
using namespace std;
#define NUM 51
int main(){
int n = 6;
int m[n+1][n+1];
int s[n + 1][n + 1];
memset(m, 0, sizeof(m));
memset(s, 0, sizeof(s));
int p[7] = {50, 10, 40, 30, 5, 20, 15};
for (int i = 1; i <= n; i++)
{
m[i][i] = 0;
}
cout << endl;
for (int r = 2; r <= n; r++)
{
int j=r;
for (int i = 1; i <= n - r + 1; i++)
{
m[i][j] = m[i][i]+m[i+1][j]+p[i-1]*p[i]*p[j];
s[i][j] = i;
for (int k = i; k < j; k++){
int t = m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if (t < m[i][j]) {
m[i][j] = t;
s[i][j] = k;
}
}
j++;
}
cout << endl;
}
for (int i = 1; i <= n; i++){
for (int j = 1; j <= n; j++){
cout << m[i][j] << " ";
}
cout << endl;
}
for (int i = 1; i <= n; i++){
for (int j = 1; j <= n; j++){
cout << s[i][j] << " ";
}
cout << endl;
}
return 0;
}
递归实现矩阵连乘
#include<iostream>
#include<cstring>
using namespace std;
int s[100][100];
int p[100];
int m[100][100];
int Recurve(int i, int j)
{
int n;
if(i==j){
return 0;
}
m[i][j] = Recurve(i, i) + Recurve(i+1, j) + p[i - 1] * p[i] * p[j];
s[i][j] = i;
for (int k = i+1; k < j;k++){
n = Recurve(i, k) + Recurve(k+1, j) + p[i - 1] * p[k] * p[j];
if(n<m[i][j]){
m[i][j] = n;
s[i][j] = k;
}
}
return m[i][j];
}
// int Recurve(int i, int j){
// if (i == j){
// return 0;
// }
// int u = Recurve(i, i)+Recurve(i+1,j)+p[i-1]*p[i]*p[j];
// s[i][j] = i;
// for (int k = i+1; k<j; k++) {
// int t = Recurve(i, k) + Recurve(k+1,j)+p[i-1]*p[k]*p[j];
// if (t<u)
// {
// u = t; s[i][j] = k;
// }
// }
// m[i][j] = u;
// return u;
// }
int main(){
int n = 6;
memset(m, 0, sizeof(m));
memset(s, 0, sizeof(s));
for (int i = 0; i <= n; i++){
cin >> p[i];
}
cout << Recurve(1, n) <<endl;
cout << m[1][n] <<endl;
for (int i = 1; i <= n;i++){
for (int j = 1; j <= n;j++){
cout << m[i][j] << " ";
}
cout << endl;
}
for (int i = 1; i <= n;i++){
for (int j = 1; j <= n;j++){
cout << s[i][j] << " ";
}
cout << endl;
}
return 0;
}
背包问题

0-1背包
#include<iostream>
using namespace std;
#define NUM 2001
int f[NUM];
int c[NUM];
int w[NUM];
int n;
int m;
int main(){
cin >> m >> n; // 容量m 物品件数n
for (int i = 1; i <= n; i++){
cin >> w[i] >> c[i];
}
for (int i = 1; i <= n; i++){
for (int v = m; v >= w[i];v--){
if(f[v]<f[v-w[i]]+c[i]){
f[v] = f[v - w[i]] + c[i];
}
}
}
for (int i = 1; i <= m;i++){
cout << f[i] << " ";
}
return 0;
}
完全背包
#include<iostream>
using namespace std;
#define NUM 2001
int f[NUM];
int c[NUM];
int w[NUM];
int n;
int m;
int main(){
cin >> m >> n; // 容量m 物品件数n
for (int i = 1; i <= n; i++){
cin >> w[i] >> c[i];
}
for (int i = 1; i <= n; i++){
for (int v = w[i]; v <= m;v++){
if(f[v]<f[v-w[i]]+c[i]){
f[v] = f[v - w[i]] + c[i];
}
}
}
for (int i = 1; i <= m; i++)
{
cout << f[i] << " ";
}
return 0;
}

