CF15E Triangles

传送门

题目大意

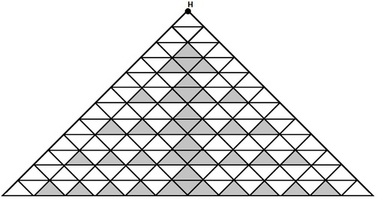
给出一个 \(n\)，求高度为 \(n\) 的，规律如下的三角形上，从顶点向下绕一圈回来，不包含黑色三角形的简单路径数，对 \(10^9+9\) 取模。

Solution

神仙思维计数，好评。

首先可以发现，这个图形是轴对称的，所以我们只考虑一半，但是这个一半比较难定义，因为最顶上有一个小三角形不能分开。于是我们把路径分成三种：

1. 特殊的绕最顶上三角形的那条路径；
2. 从左边下去绕回来到达最顶上的黑色三角形的顶端；
3. 从右边下去绕回来到达最顶上的黑色三角形的顶端；

发现第一条单独算掉，后面两条的答案是一样的，并且可以两两组合成为一条完整的路径。不妨设左右下去回来的路径方案数为 \(ans\)，那么最终的答案就是 \(ans^2\times 2+2\)，两两组合方案为 \(ans^2\)，考虑方向再乘个 \(2\)，然后加上一条特殊路径。

然后我们刨掉一半后来思考这个问题。首先我必然是沿着最左边的那一条线向下，然后中间一条过渡过来，不妨称这条边为过渡边，然后贴着高低不平的黑色大三角的外缘上来。我们方案数主要由过渡边的选择和向黑色大三角内延伸多少。可以发现过渡边是唯一的，而黑色三角形内延伸进去的方案数是固定的，因此可以很方便地求出总方案数。

具体地，我们主要考虑每一个凹进去的黑色边，会产生多少方案。容易得到，原图中 \(4\sim 6\) 行凹进去那一块的方案数是 \(5\)，然后再向下两行的方案数是 \(13\)，怎么算的？可以把里面的当成是上一行的东西，那么考虑最外层的，在 \(5\) 种方案中能到达里面的有 \(3\) 种，加上剩下的两种。这样可以递推求出每个凹形对方案的贡献。然后考虑过渡边。我们发现每条过渡边的方案数就是它上方的凹形方案乘积。反过来，每个凹形只对下面的过渡边产生贡献。并且我们发现，\(4\) 个一组的过渡边的方案数是一样的，所以可以合起来，就轻易求出了最终的 \(ans\)。

然后直接算答案就可以了。

Code

// Problem: CF15E Triangles
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF15E
// Memory Limit: 62.5 MB
// Time Limit: 1000 ms
// Author: ZCETHAN
// Time: 2021-11-08 16:38:04

#include<bits/stdc++.h>
#define ll long long
#define inf (1<<30)
#define INF (1ll<<60)
using namespace std;
const int MAXN=1e6+10;
const ll MOD=1e9+9;
ll dp[MAXN];
int main()
{
	int n;
	scanf("%d",&n);
	dp[1]=1;
	for(int i=2;i<=n/2;i++)
		dp[i]=(dp[i-1]*2%MOD+3)%MOD;//推算每个凹形的方案
	for(int i=2;i<=n/2;i++)
		dp[i]=dp[i]*dp[i-1]%MOD;//前缀积表示每一组过渡边的方案数
	ll ans=2;
	for(int i=2;i<=n/2;i++)
		ans=(ans+dp[i-1]*4%MOD)%MOD;//4 个一组加起来
	printf("%lld\n",(ans*ans%MOD*2%MOD+2)%MOD);//直接算答案
	return 0;
}