学习笔记——Kruskal 重构树

引入

大家都知道 \(Kruskal\) 求最小生成树吧，这个算法就是建立在前面说的算法的基础上的一个奇妙的想法。
有这么一个问题，给你一张图，每条边都有权值，然后规定一堆东西后问：满足条件的路径中，所经过边权最大值最小是多少。

初步想法

二分，一定是最先想到的，我们接下来就以标题中的那题为例讲讲这个算法。

我们很容易想到二分最大边权，然后验证。但是每次验证都跑 \(dfs\) 肯定得炸。
那么怎么办呢。

来看看重构树算法的实现吧。

实现

首先，根据 \(Kruskal\) 的贪心思路，如果我从 \(x\) 节点出发，有较小的边可以走，肯定是不会走较大的边的，换句话说，就是一定是在图的最小生成树上走最优。

所以无疑，算法第一步：将边按权排序，求出最小生成树。

然后在求的过程中，就是本算法的构造了。对于我当前枚举的边所连接的两个点(或者点集)，用一个虚拟节点建在上方作为这两个点的父节点，然后将这个父节点的权值赋为边的权值。

也许不是很清楚，那么来看看题目中样例这个图：
(注意本题是把编号当成边权的)

和 \(Kruskal\) 一样，先取出 \(Edge(2,3)\)，然后建立一个父子关系，加入到同一集合里。已经有 \(5\) 个点了，所以他们的父节点就记为 \(6\)，权值为 \(1\)。

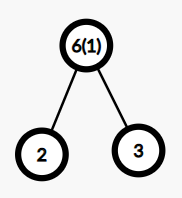
然后是 \(Edge(4,5)\)，进行同样的操作。

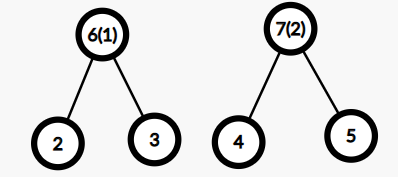
然后是 \(Edge(2,1)\)，但是此时 \(2\) 已经属于一个点集了，所以实质上是把 \(1\) 和 \(2\) 所在的点集连起来，所以应该是连结 \((1,6)\)。

然后查到 \(Edge(1,3)\)，但是在前面的并查集中可以查到，\(1\) 和 \(3\) 已经在同一集合里了，所以跳过。
所以最后一条边是 \(Edge(1,4)\)，实质是把 \(8,7\) 连起来。
其他的都会跳过，因为已经合并好了。

然后就可以在这棵树上做一些奇奇怪怪的操作了，因为它有一个美妙的性质：每一条树枝上，边权是单调的，那么可以倍增来快速找到最大的不超过某个值的最小位置是哪里了。

比如本题，就可以二分答案，然后对于 \(x\) 和 \(y\)，分别向上跳到点权是大于我二分的值为止，然后向下子树中叶节点个数一加就是我经过点的个数，和 \(z\) 比一下，就可以实现这个二分了。
\(\color{Red}{Ps:}\) 一定一定一定要注意倍增不要写错以及，如果 \(xy\) 跳到一起去了，只能算一个。

相信理解起来不难吧。上代码。

Code

#include<bits/stdc++.h>
#define ll long long
#define inf 1<<30
using namespace std;
const int MAXN=2e5+10;
vector<int> vec[MAXN];
void add(int fa,int u,int v){
	vec[fa].push_back(u);
	vec[fa].push_back(v);
}
int cnt,son[MAXN],f[MAXN][20],v[MAXN];
void dfs(int x,int fa){
	f[x][0]=fa;
	for(int i=1;i<20;i++) f[x][i]=f[f[x][i-1]][i-1];
	if(vec[x].size()==0){son[x]=1;return;}
	son[x]=0;
	for(int i=0;i<vec[x].size();i++){
		int s=vec[x][i];
		if(s==fa) continue;
		dfs(s,x);son[x]+=son[s];
	}
}//预处理倍增和子树中叶节点的个数
int check(int p,int x,int y){
	for(int i=19;i>=0;i--){
		if(v[f[x][i]]<=p) x=f[x][i];
		if(v[f[y][i]]<=p) y=f[y][i];
	}
	if(x==y) return son[x];
	else return son[x]+son[y];
}//验算，得到经过节点个数
int ff[MAXN];
int find(int x){return ff[x]==x?x:ff[x]=find(ff[x]);}
int main()
{
	int n,m,x,y,z;
	scanf("%d%d",&n,&m);cnt=n;
	for(int i=1;i<=2*n;i++) v[i]=0,ff[i]=i;
	v[0]=inf;//防止跳到根的外面去
	for(int i=1;i<=m;i++){
		scanf("%d%d",&x,&y);
		int fx=find(x),fy=find(y);
		if(cnt<n*2-1&&fx!=fy){
			cnt++;
			v[cnt]=i;
			ff[fy]=cnt;
			ff[fx]=cnt;//这里其实和裸的Kruskal很像的，但是由于有新建的节点所以更优美了
			add(cnt,fx,fy);
		}//本题的特殊性，否则需要按权排序后再做
	}
	dfs(cnt,0);int Q;
	for(scanf("%d",&Q);Q--;){
		scanf("%d%d%d",&x,&y,&z);
		int ans=m,l=0,r=m;
		while(l<=r){
			int mid=l+r>>1;
			if(check(mid,x,y)<z) l=mid+1,ans=l;
			else r=mid-1;
		}
		printf("%d\n",ans);
	}
}

END

很多人用可持久化并查集和整体二分过了这题……