学习笔记——虚树
模板题引入
先来看一道模板题，CF 上的。
这题的意思是给定一棵有 \(n\) 个节点的树，树上有一些关键点（\(key\)）。接下来有 \(q\) 组询问，每次给出 \(k_i\) 个 \(key\)，要求删去一些点，使得这些 \(key\) 不相连。要求删去的最少的点数。
模板题解析
第一眼看到这题，先想到的肯定是树形 \(dp\)。毕竟是在树上嘛。但是接下来看了一眼范围 \(1\le n\le 100000\)，而且 \(1\le q\le 100000\)。如果对于每个 \(q\) 都跑一次完整的树，那么显然，\(O(n\times q)\) 一算就会 \(TLE\)。
那么我们可以先不考虑这个，先想怎么 \(dp\)。很简单，运用贪心，分类。
如果当前节点是关键点，那么查询它是否有子儿子是关键点，如果有，那么显然连向这个子节点的链上需要被截断，否则就不用。
如果不是关键点，那么如果子树中有关键点并且多于 \(2\) 个，那么显然，把当前节点删掉会最优，如果只有一个，那么留到后面和其他子树中的关键点分割更优。
因此，设当前节点是 \(x\)，它的儿子是 \(son\)，定义 \(dp[i]\) 表示以 \(i\) 为根的子树，使得所有的 \(key\) 都不连通的最小删点个数，\(siz[i]\) 表示以 \(i\) 为根的子树里 \(key\) 的个数。则有：
\(if(x\;is\;key)\)
\(\qquad dp[x]+=dp[son];\)
\(\qquad\qquad if(siz[son]) ans[x]++;\)
\(else\)
\(\qquad ans[x]+=ans[son];\)
\(\qquad siz[x]+=siz[son];\)
\(\qquad\cdots\)
\(\qquad if(siz[x]>1)\)
\(\qquad\qquad siz[x]=0;\)
\(\qquad\qquad ans[x]++;\)
无解很简单，只有当两个 \(key\) 相连的时候是无解的。
虚树
接下来我们考虑一开始提出的问题。
读题几遍后发现：
因此如果我们只考虑 \(key\)，那么是十分快的，只有\(O(k)\)。所以我们随便建了一棵树，并写了几个 \(key\)。
那么显然，结果只和 \(key\) 有关，因此我们可以将其压缩，只保留红色节点即可。
但是马上发现，只留下蓝色和红色的，会发现不够啊，如果只有红色的节点，无法使得节点之间的父子关系显示出来，无法很好地 \(dp\)。因此下面这个绿色的点也需要保留，以表示绿色下面的是其儿子，从而传递。
多写几棵树，就可以发现，其实只要把 \(key\) 和几个 \(key\) 的 \(LCA\) 保留，就可以维护树的形状，又能简化树，使得 \(dp\) 的复杂度大大降低。
此时就变成了删边使得每个 \(key\) 都不相连。(判断无解只要在简化之前做就可以了，这样每个 \(key\) 之间都会有点可以删，就可以变成删边)
像这样建出来的只保留 \(key\) 的树，称之为虚树。
虚树通常是树形 \(dp\) 时常用的优化操作。上面这棵树简化后是这样的：
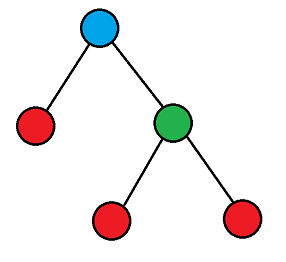
看，是不是简单了很多呢？
建虚树
首先需要建出实树，然后算出 \(dfs\) 序的编号，然后求 \(LCA\)，将 \(LCA\) 也加入到虚树里即可。那么 \(LCA\) 选用倍增的方式求，要求出每个节点的 \(deep\)。当然也可以不用倍增，只要能求出来就好。
建实树，\(fa\) 是倍增用的。(别问怎么又是这个 \(QAQ\))
void QAQ(int x,int f,int depth)
{
ldfn[x]=++cnt;//顺搜的dfn
dep[x]=depth;//深度
fa[x][0]=f;//x节点向上跳2^0步就是它的父节点
for(int i=1;i<20;i++)
fa[x][i]=fa[fa[x][i-1]][i-1];
for(int i=0;i<rea[x].size();i++)//遍历实树
if(rea[x][i]!=f)
QAQ(rea[x][i],x,depth+1);
rdfn[x]=cnt;//回溯的dfn，后文会讲为什么要存回溯的
}
求 \(LCA\)，倍增的板子。
int LCA(int x,int y)
{
if(dep[x]<dep[y]) swap(x,y);
int delta=dep[x]-dep[y];
for(int i=0;i<20&δi++)
if(delta&(1<<i))
x=fa[x][i];
if(x==y) return x;
for(int i=19;i>=0;i--)
if(fa[x][i]!=fa[y][i]){
x=fa[x][i];
y=fa[y][i];
}
return fa[x][0];
}//?不会有人还不知道倍增吧，不会吧不会吧。
接下来就是比较困难的建虚树。首先我们要理解其原理。
先把元素按 \(ldfn\) 排序。维护一个树链，对于一个待插入的元素，在当前的树链上找，找到第一个这个元素的祖先，就把这个元素插入到这个祖先的子树里去即可。
原理非常简单，但是怎么实现呢？首先观察一个元素的祖先唯一满足什么条件。不妨对于上面的树，我们算一下 \(ldfn\) 和 \(rdfn\)，以数对 \((ldfn,rdfn)\) 的形式列出来，然后找规律。
注意，回溯的时候编号不加一。
我们可以发现，对于一条树链，一个节点 \(a\) 如果是节点 \(b\) 的祖先，那么必定是 \(rdfn[a]\ge ldfn[b]\)，反之也成立。原因很简单，因为枚举到当前节点的时候，它的祖先节点的 \(rdfn\) 还没有算，要等到这棵子树遍历完后再赋值，那么肯定是比当前节点大的。[1]
接下来就是怎么维护树链了。只要维护一个从底到顶深度不断增加的单调栈即可。每次将当前元素与栈顶元素比较，如果不满足栈顶元素是当前元素的祖先，那么弹出当前栈顶元素直到满足为止，然后将当前元素压入栈，再维护一条新的链。由于元素已经排序，所以肯定是从左到右建立所有的链。
接下来考虑一个问题，\(LCA\)如果每对元素都求的话，复杂度还是很高。因此我们要考虑简化。探索后发现，只要求相邻两个元素的 \(LCA\)，由于是按 \(ldfn\) 排序了的元素，这样的 \(LCA\) 肯定覆盖了所有需要的节点，因此只要扫一遍然后怼出 \(LCA\) 即可。
接下来手动模拟一次，以上面的树为例：
接下来看弹出。
看，是不是一样建出来了！看官可以自行造几组样例，按上面的表述去建一建虚树。
接下来给出代码：
bool cmp(int x,int y)
{
return ldfn[x]<ldfn[y];
}//按dfn排序
void build()
{
sort(d+1,d+1+m,cmp);
int keynum=m;
for(int i=1;i<keynum;i++)
d[++m]=LCA(d[i],d[i+1]);//求相邻两个的LCA
sort(d+1,d+1+m,cmp);
m=unique(d+1,d+1+m)-d-1;
//去重，unique对一个已经排序的数组可以实现去重，
//多出来的扔到了数组的后面，并返回数组大小的地址
int top=0;
stk[++top]=d[1];
for(int i=2;i<=m;i++){
while(top&&rdfn[stk[top]]<ldfn[d[i]])
top--;//如果不是祖先，则弹出元素
if(top) vir[stk[top]].push_back(d[i]);//加入到其祖先的子树里
stk[++top]=d[i];//维护新的链
}
}
这样，我们就可以很好地解决复杂度过大的问题了。
给出模板题的标程：带注释
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN=1e5+100;
int cnt,m;
int ldfn[MAXN],rdfn[MAXN],fa[MAXN][20],dep[MAXN],stk[MAXN],d[MAXN],vis[MAXN];
vector<int> rea[MAXN],vir[MAXN];
int ans[MAXN],siz[MAXN];
void QAQ(int x,int f,int depth)
{
ldfn[x]=++cnt;
dep[x]=depth;
fa[x][0]=f;
for(int i=1;i<20;i++)
fa[x][i]=fa[fa[x][i-1]][i-1];
for(int i=0;i<rea[x].size();i++)
if(rea[x][i]!=f)
QAQ(rea[x][i],x,depth+1);
rdfn[x]=cnt;
}
int LCA(int x,int y)
{
if(dep[x]<dep[y]) swap(x,y);
int delta=dep[x]-dep[y];
for(int i=0;i<20&δi++)
if(delta&(1<<i))
x=fa[x][i];
if(x==y) return x;
for(int i=19;i>=0;i--)
if(fa[x][i]!=fa[y][i]){
x=fa[x][i];
y=fa[y][i];
}
return fa[x][0];
}
bool cmp(int x,int y)
{
return ldfn[x]<ldfn[y];
}
void build()
{
sort(d+1,d+1+m,cmp);
int keynum=m;
for(int i=1;i<keynum;i++)
d[++m]=LCA(d[i],d[i+1]);
sort(d+1,d+1+m,cmp);
m=unique(d+1,d+1+m)-d-1;
int top=0;
stk[++top]=d[1];
for(int i=2;i<=m;i++){
while(top&&rdfn[stk[top]]<ldfn[d[i]])
top--;
if(top) vir[stk[top]].push_back(d[i]);
stk[++top]=d[i];
}
}
void dfs(int x)
{
ans[x]=0;
if(vis[x]){
siz[x]=1;
for(int i=0;i<vir[x].size();i++){
int son=vir[x][i];
dfs(son);
ans[x]+=ans[son];
if(siz[son]) ans[x]++;
}
}
else{
siz[x]=0;
for(int i=0;i<vir[x].size();i++){
int son=vir[x][i];
dfs(son);
ans[x]+=ans[son];
siz[x]+=siz[son];
}
if(siz[x]>1){
siz[x]=0;
ans[x]++;
}
}
}
int main()
{
int n,q,u,v;
while(~scanf("%d",&n)){
for(int i=0;i<=n;i++)
rea[i].clear();
for(int i=1;i<n;i++){
scanf("%d%d",&u,&v);
rea[u].push_back(v);
rea[v].push_back(u);
}
cnt=0;
QAQ(1,0,0);
scanf("%d",&q);
while(q--){
scanf("%d",&m);
for(int i=1;i<=m;i++){
scanf("%d",&d[i]);
vis[d[i]]=1;
}
int fl=1;
for(int i=1;i<=m;i++)
if(vis[fa[d[i]][0]]){
fl=0;break;
}
if(!fl) puts("-1");
else{
build();dfs(d[1]);
printf("%d\n",ans[d[1]]);
}
for(int i=1;i<=m;i++)
vis[d[i]]=0,vir[d[i]].clear();
}
}
}
例题一枚
非常经典的，虚树必刷的消耗战，洛谷上的链接。
其实就是上面题的简化版，要求所有的 \(key\) 都不与 \(1\) 连通。同样的先摆好 \(dp\)，再想建虚树。直接看代码注释吧。
#include<bits/stdc++.h>
#define ll long long
#define inf 1ll<<60
using namespace std;
const int MAXN=250010;
struct node{
ll to,w;
node(){}
node(ll _to,ll _w){
to=_to,w=_w;
}
};//注意实树里要存边权值
ll m,cnt,ldfn[MAXN],rdfn[MAXN],dep[MAXN],fa[MAXN][20],d[MAXN<<1];
ll stk[MAXN],dp[MAXN],w[MAXN];
//dp[i]表示i的子树割断的最小花费
bool vis[MAXN];
vector<node> rea[MAXN];
vector<ll> vir[MAXN];
void QAQ(ll x,ll f,ll depth)
{
ldfn[x]=++cnt;
dep[x]=depth;
fa[x][0]=f;
for(ll i=1;i<20;i++)
fa[x][i]=fa[fa[x][i-1]][i-1];
for(ll i=0;i<rea[x].size();i++)
if(rea[x][i].to!=f){
w[rea[x][i].to]=min(w[x],rea[x][i].w);
//由于只要隔断1，因此维护每个节点到1的最短边割断即可
QAQ(rea[x][i].to,x,depth+1);
}
rdfn[x]=cnt;
}
ll LCA(ll x,ll y)
{
if(dep[x]<dep[y]) swap(x,y);
ll delta=dep[x]-dep[y];
for(ll i=0;i<20&δi++)
if(delta&(1<<i))
x=fa[x][i];
if(x==y) return x;
for(ll i=19;i>=0;i--)
if(fa[x][i]!=fa[y][i]){
x=fa[x][i];
y=fa[y][i];
}
return fa[x][0];
}
bool cmp(ll x,ll y){return ldfn[x]<ldfn[y];}
void build()
{
sort(d+1,d+1+m,cmp);
ll keynum=m;
for(ll i=1;i<keynum;i++)
d[++m]=LCA(d[i],d[i+1]);
d[++m]=1;
sort(d+1,d+1+m,cmp);
m=unique(d+1,d+1+m)-d-1;
ll top=0;
stk[++top]=d[1];
for(ll i=2;i<=m;i++){
while(top&&rdfn[stk[top]]<ldfn[d[i]])
top--;
if(top) vir[d[i]].push_back(stk[top]),
vir[stk[top]].push_back(d[i]);
stk[++top]=d[i];
}
}//板子
void dfs(ll x,ll fa)
{
if(vir[x].size()<=0&&vis[x]){
dp[x]=inf;//叶节点并且不是key，则不用考虑，因此为inf
return;
}
for(ll i=0;i<vir[x].size();i++){
ll son=vir[x][i];
if(son==fa) continue;
dfs(son,x);
if(vis[son]) dp[x]+=w[son];//如果儿子是key，那么显然要把这个儿子割断
else dp[x]+=min(w[son],dp[son]);//否则可以考虑割断儿子的其他子树会更小
}
}
int main()
{
ll n,u,v,t,q;
scanf("%lld",&n);
for(ll i=1;i<n;i++){
scanf("%lld%lld%lld",&u,&v,&t);
rea[u].push_back(node(v,t));
rea[v].push_back(node(u,t));
}
cnt=0;w[1]=inf;
QAQ(1,0,0);
// for(int i=1;i<=n;i++) cerr<<w[i]<<' ';
scanf("%lld",&q);
while(q--){
scanf("%lld",&m);
for(ll i=1;i<=m;i++) scanf("%lld",&d[i]),vis[d[i]]=1;
build();
dfs(d[1],-1);
printf("%lld\n",dp[1]);
for(ll i=1;i<=m;i++) dp[d[i]]=0,vis[d[i]]=0,vir[d[i]].clear();
//精准扶贫，防TLE
}
}
其实消耗战才是模板题，只是因为它有关权值，所以把它放到应用。
总结
虚树和矩阵快速幂一样，是优化型的算法。使用虚树的条件：
- 有关键点，且关键点的数量少。
- 有必要。显然，如果裸的 \(dp\) 可以跑，为什么要敲个虚树的板子呢？
以此记录虚树的学习。
这里可以回答上面注释里的问题了，由于只维护 \(ldfn\) 会产生混淆，比如上面的 \((8,8)\) 就会放到 \((7,7)\) 的下面而不是 \((6,8)\) 的儿子。 ↩︎
