【BZOJ4800】[CEOI2015 Day2]世界冰球锦标赛 (折半搜索)
[CEOI2015 Day2]世界冰球锦标赛
题目描述
译自 CEOI2015 Day2 T1「Ice Hockey World Championship」
今年的世界冰球锦标赛在捷克举行。\(Bobek\) 已经抵达布拉格,他不是任何团队的粉丝,也没有时间观念。他只是单纯的想去看几场比赛。如果他有足够的钱,他会去看所有的比赛。不幸的是,他的财产十分有限,他决定把所有财产都用来买门票。
给出 \(Bobek\) 的预算和每场比赛的票价,试求:如果总票价不超过预算,他有多少种观赛方案。如果存在以其中一种方案观看某场比赛而另一种方案不观看,则认为这两种方案不同。
输入输出格式
输入格式:
第一行,两个正整数 \(N\) 和 \(M(1 \leq N \leq 40,1 \leq M \leq 10^{18})\),表示比赛的个数和 \(Bobek\) 那家徒四壁的财产。
第二行,\(N\) 个以空格分隔的正整数,均不超过 \(10^{16}\),代表每场比赛门票的价格。
输出格式:
输出一行,表示方案的个数。由于 \(N\) 十分大,注意:答案 \(\le 2^{40}\)。
输入输出样例
输入样例#1:
5 1000
100 1500 500 500 1000
输出样例#1:
8
说明
样例解释
八种方案分别是:
- 一场都不看,溜了溜了
- 价格 \(100\) 的比赛
- 第一场价格 \(500\) 的比赛
- 第二场价格 \(500\) 的比赛
- 价格 \(100\) 的比赛和第一场价格 \(500\) 的比赛
- 价格 \(100\) 的比赛和第二场价格 \(500\) 的比赛
- 两场价格 \(500\) 的比赛
- 价格 \(1000\) 的比赛
有十组数据,每通过一组数据你可以获得 \(10\) 分。各组数据的数据范围如下表所示:
| 数据组号 | 1-2 | 3-4 | 5-7 | 8-10 |
|---|---|---|---|---|
| $N \leq $ | \(10\) | \(20\) | \(40\) | \(40\) |
| \(M \leq\) | \(10^6\) | \(10^{18}\) | \(10^6\) | \(10^{18}\) |
题解
首先看数据范围
-
1-4组数据\(N\leq20\),爆搜就可以解决。
inline void dfs(R ll dep,R ll sum){ if(sum>m)return; if(dep==n+1){ ans++; return; } dfs(dep+1,sum+a[dep]); dfs(dep+1,sum); } int main(){ read(n);read(m); for(R int i=1;i<=n;i++)read(a[i]); if(n<=20){ dfs(1,0); printf("%lld\n",ans); } return 0; } -
5-7组数据\(M\leq10^6\),裸的背包啊。
int main(){ read(n);read(m); for(R int i=1;i<=n;i++)read(a[i]); if(m<=1e6){ f[0]=1; for(R int i=1;i<=n;i++) for(R int j=m;j>=a[i];j--) f[j]+=f[j-a[i]]; for(R int i=0;i<=m;i++)ans+=f[i]; printf("%lld\n",ans); } return 0; } -
现在你已经能拿到70分了(但在洛谷上是47分)
下面引出主角——折半搜索(meet in the middle思想)
因为\(N\leq40\) \(O(2^{40})\)的爆搜一定会\(TLE\),所以我们将\(N\)分成两份
搜索\(1\)到\(n/2\)和\(n/2+1\)到\(n\),让复杂度降到\(O(2^{n/2+1})\)。
画一个图(网上找的不错的图)理解一下为什么能降低复杂度

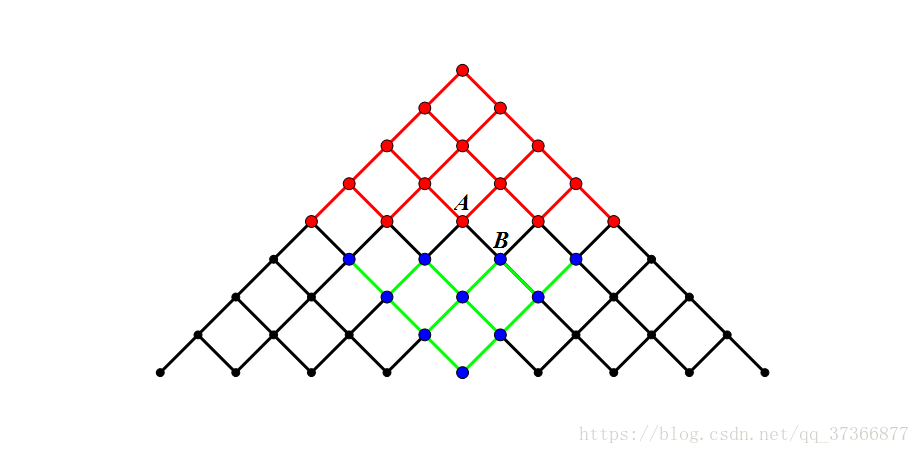
inline void dfs(R int l,R int r,R ll sum,R ll a[],R ll &cnt){
if(sum>m)return;
if(l>r){
a[++cnt]=sum;
return;
}
dfs(l+1,r,sum+w[l],a,cnt);//选
dfs(l+1,r,sum,a,cnt);//不选
}
将前一半的搜索状态存入a数组,后一半存入b数组。
mid=n/2;
dfs(1,mid,0,suma,cnta);
dfs(mid+1,n,0,sumb,cntb);
一般\(meet\) \(in\) \(the\) \(middle\)的难点主要在于最后答案的组合统计。
我们可以现将a或b数组sort,让其有序。
然后通过枚举另一个数组中的状态,来实现统计答案。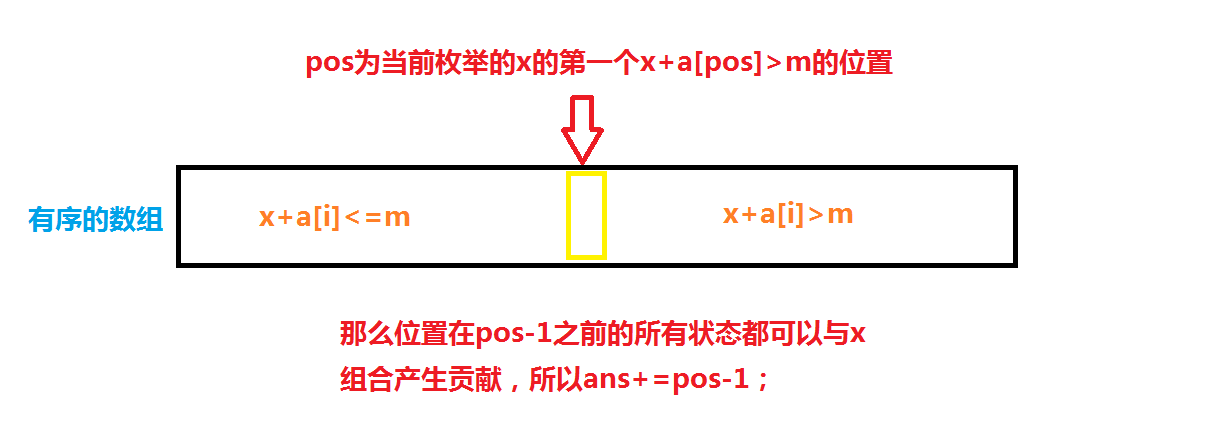
上述找\(pos\)的过程可以通过upper_bound()完成。
sort(suma+1,suma+1+cnta);//使一个数组有序
for(R int i=1;i<=cntb;i++)
ans+=upper_bound(suma+1,suma+1+cnta,m-sumb[i])-suma-1;//统计ans
下面是高清完整code:
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cctype>
#define ll long long
#define R register
#define N 55
using namespace std;
template<typename T>inline void read(T &a){
char c=getchar();T x=0,f=1;
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
a=f*x;
}
ll n,m,w[N],mid,suma[1<<21],sumb[1<<21],cnta,cntb,ans;
inline void dfs(R int l,R int r,R ll sum,R ll a[],R ll &cnt){
if(sum>m)return;
if(l>r){
a[++cnt]=sum;
return;
}
dfs(l+1,r,sum+w[l],a,cnt);
dfs(l+1,r,sum,a,cnt);
}
int main(){
read(n);read(m);
for(R int i=1;i<=n;i++)read(w[i]);
mid=n>>1;
dfs(1,mid,0,suma,cnta);
dfs(mid+1,n,0,sumb,cntb);
sort(suma+1,suma+1+cnta);
for(R int i=1;i<=cntb;i++)
ans+=upper_bound(suma+1,suma+1+cnta,m-sumb[i])-suma-1;
printf("%lld\n",ans);
return 0;
}


