【NOIP 2009】最优贸易
描述
C 国有 n 个大城市和 m 条道路,每条道路连接这 n 个城市中的某两个城市。任意两个
城市之间最多只有一条道路直接相连。这 m 条道路中有一部分为单向通行的道路,一部分
为双向通行的道路,双向通行的道路在统计条数时也计为 1 条。
C 国幅员辽阔,各地的资源分布情况各不相同,这就导致了同一种商品在不同城市的价
格不一定相同。但是,同一种商品在同一个城市的买入价和卖出价始终是相同的。
商人阿龙来到 C 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息
之后,便决定在旅游的同时,利用商品在不同城市中的差价赚回一点旅费。设 C 国 n 个城
市的标号从 1~ n,阿龙决定从 1 号城市出发,并最终在 n 号城市结束自己的旅行。在旅游的
过程中,任何城市可以重复经过多次,但不要求经过所有 n 个城市。阿龙通过这样的贸易方
式赚取旅费:他会选择一个经过的城市买入他最喜欢的商品——水晶球,并在之后经过的另
一个城市卖出这个水晶球,用赚取的差价当做旅费。由于阿龙主要是来 C 国旅游,他决定
这个贸易只进行最多一次,当然,在赚不到差价的情况下他就无需进行贸易。
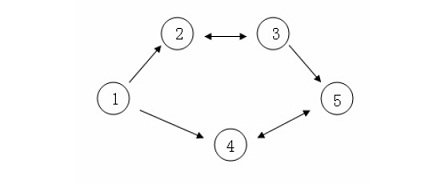
假设 C 国有 5 个大城市,城市的编号和道路连接情况如下图,单向箭头表示这条道路
为单向通行,双向箭头表示这条道路为双向通行。
假设 1~n 号城市的水晶球价格分别为 4,3,5,6,1。
阿龙可以选择如下一条线路:1->2->3->5,并在 2 号城市以 3 的价格买入水晶球,在 3
号城市以 5的价格卖出水晶球,赚取的旅费数为 2。
阿龙也可以选择如下一条线路 1->4->5->4->5,并在第 1 次到达 5 号城市时以 1 的价格
买入水晶球,在第 2 次到达 4 号城市时以 6 的价格卖出水晶球,赚取的旅费数为 5。
现在给出 n个城市的水晶球价格,m条道路的信息(每条道路所连接的两个城市的编号
以及该条道路的通行情况) 。请你告诉阿龙,他最多能赚取多少旅费。
格式
输入格式
第一行包含 2 个正整数 n 和 m,中间用一个空格隔开,分别表示城市的数目和道路的
数目。
第二行 n 个正整数,每两个整数之间用一个空格隔开,按标号顺序分别表示这 n 个城
市的商品价格。
接下来 m行, 每行有 3 个正整数, x, y, z, 每两个整数之间用一个空格隔开。 如果 z=1,
表示这条道路是城市 x到城市 y之间的单向道路;如果 z=2,表示这条道路为城市 x 和城市
y之间的双向道路。
输出格式
输出共1 行, 包含 1 个整数, 表示最多能赚取的旅费。 如果没有进行贸易,
则输出 0。
样例1
样例输入1
5 5
4 3 5 6 1
1 2 1
1 4 1
2 3 2
3 5 1
4 5 2 样例输出1
5限制
每个测试点1s
输入数据保证 1 号城市可以到达n 号城市。
对于 10%的数据,1≤n≤6。
对于 30%的数据,1≤n≤100。
对于 50%的数据,不存在一条旅游路线,可以从一个城市出发,再回到这个城市。
对于 100%的数据,1≤n≤100000,1≤m≤500000,1≤x,y≤n,1≤z≤2,1≤各城市
水晶球价格≤100。
题解
此题好多人都用最短路写的,但我觉得用搜索就足以了(虽然本质差不多)。
建图:
此题需要建一个正向图(e1)和一个反向图(e2);
下面讲解为什么。
BFS:
正向图从1点开始搜并更新buy[](取min),反向图从n点开始搜sell[](取max);
从n点跑反向图是因为此题要求一定要先买后卖;
buy[i]表示到i点最小买入;sell[i]表示到i点最大卖出;
queue<int> q; void bfs1(int u){ memset(buy,0x3f,sizeof(buy)); memset(vis,0,sizeof(vis)); q.push(u); while(!q.empty()){ int x=q.front();q.pop(); if(vis[x])continue;vis[x]=1; for(int i=h1[x];i;i=e1[i].nex){ int xx=e1[i].to; buy[xx]=min(a[xx],buy[x]); q.push(xx); } } } void bfs2(int u){ memset(sell,-0x3f,sizeof(sell)); memset(vis,0,sizeof(vis)); q.push(u); while(!q.empty()){ int x=q.front();q.pop(); if(vis[x])continue;vis[x]=1; for(int i=h2[x];i;i=e2[i].nex){ int xx=e2[i].to; sell[xx]=max(a[xx],sell[x]); q.push(xx); } } }
code:
代码应该不算长
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cctype> 5 #include<queue> 6 #define ll long long 7 using namespace std; 8 const int N=1100000; 9 int read() 10 { 11 int X=0,w=0; char ch=0; 12 while(!isdigit(ch)) {w|=ch=='-';ch=getchar();} 13 while(isdigit(ch)) X=(X<<3)+(X<<1)+(ch^48),ch=getchar(); 14 return w?-X:X; 15 } 16 int n,m,a[N],h1[N],h2[N],ans,tot,buy[N],sell[N]; 17 bool vis[N]; 18 struct node{ 19 int nex,to; 20 }e1[N],e2[N]; 21 void add(int u,int v){ 22 e1[++tot].nex=h1[u]; 23 e1[tot].to=v; 24 h1[u]=tot; 25 e2[tot].nex=h2[v]; 26 e2[tot].to=u; 27 h2[v]=tot; 28 } 29 queue<int> q; 30 void bfs1(int u){ 31 memset(buy,0x3f,sizeof(buy)); 32 memset(vis,0,sizeof(vis)); 33 q.push(u); 34 while(!q.empty()){ 35 int x=q.front();q.pop(); 36 if(vis[x])continue;vis[x]=1; 37 for(int i=h1[x];i;i=e1[i].nex){ 38 int xx=e1[i].to; 39 buy[xx]=min(a[xx],buy[x]); 40 q.push(xx); 41 } 42 } 43 } 44 void bfs2(int u){ 45 memset(sell,-0x3f,sizeof(sell)); 46 memset(vis,0,sizeof(vis)); 47 q.push(u); 48 while(!q.empty()){ 49 int x=q.front();q.pop(); 50 if(vis[x])continue;vis[x]=1; 51 for(int i=h2[x];i;i=e2[i].nex){ 52 int xx=e2[i].to; 53 sell[xx]=max(a[xx],sell[x]); 54 q.push(xx); 55 } 56 } 57 } 58 signed main() 59 { 60 scanf("%d%d",&n,&m); 61 for(int i=1;i<=n;i++)a[i]=read(); 62 for(int i=1;i<=m;i++){ 63 int x,y,z; 64 x=read();y=read();z=read(); 65 if(z==1)add(x,y); 66 if(z==2)add(x,y),add(y,x); 67 } 68 bfs1(1); 69 bfs2(n); 70 for(int i=1;i<=n;i++) 71 ans=max(sell[i]-buy[i],ans); 72 printf("%d",ans); 73 return 0; 74 }
-^-^--ZAGER--^-^-


 浙公网安备 33010602011771号
浙公网安备 33010602011771号