[JXOI2017] 颜色

思路

容易转化到枚举区间使得区间中的颜色都被全部选择

考虑优化
联想到数据结构处理点对贡献

考虑枚举右端点 \(r\) , 求有多少种 \(l\) 是满足条件的

首先对于 \(r\) 右边出现过的颜色, 区间中一定不能包含
令每个颜色最右边的出现位置为 \(mxp_i\) , 则有 \(\forall j \in [l, r] , r \geq mxp_{col_j} \ (1)\)

其次对于 \(l\) 左边出现过的颜色, 区间中一定不能包含
令每个颜色最左边的出现位置为 \(mnp_i\) , 则有 \(\forall j \in [l, r] , l \leq mnp_{col_j} \ (2)\)

这些约束条件怎么高效的处理成为了现在的问题

把 \(r\) 从右到左枚举, 容易发现的是随着 \(r\) 的移动, 我们动态处理
具体的, 每次到达一个颜色的 \(mxp_i\) 才将 \([1, mnp_i]\) 记录为可行

感觉已经完成了, 我们模拟一遍样例检查一下

观察发现显然是不能这样做的, 原因是你必须保证前面的其他颜色也符合要求

我们需要把 "每次到达一个颜色的 \(mxp_i\) 才将 \([1, mnp_i]\) 记录为可行" 变成在对于之前访问过的所有 \(mxp_i\) 中最广的 \([1, mnp_i]\)

这个显然可以堆上处理, 事实上我们可以单调栈优化, 这个很显然

---

妈妈生的, 复习

题意

给定颜色序列 $col$ , 求有多少区间 $[L, R]$ 满足
对于 $col_i \in [L, R]$ , $col$ 中所有的 $col_i$ 都在 $[L, R]$ 中

怎么统计?
不难发现对于一个颜色 \(i\) , 处理出其最远点对 \(\{p_{i, 1}, p_{i, 2}\}\)
那么每个合法区间要么包含, 要么与最远点对无交

形式化上面的约束,

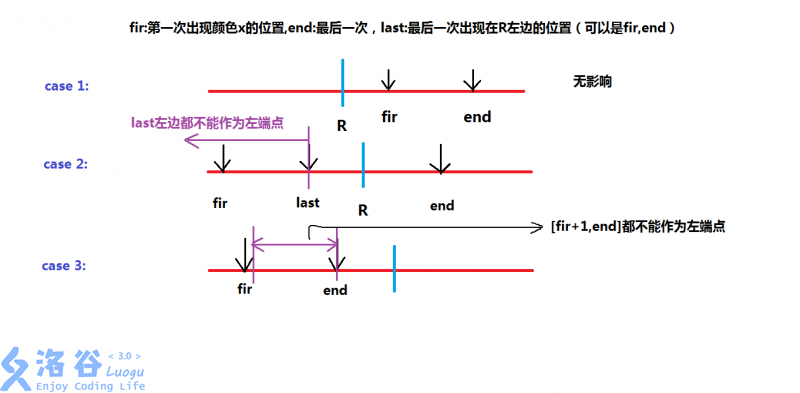
不难发现我们要找到

• 所有 \(p_{i, 2} > R\) 的颜色 \(i\) 中, \(last\) 最大的一个
• 所有 \(p_{i, 2} \leq R\) 的颜色 \(i\) 对应的 \(\{p_{i, 1}, p_{i, 2}\}\)

我们维护 \(\{last, p_{i, 2}\}\) 的单调栈, 找到一个 \(i\) 把 \(\{pos_i, p_{i, 2}\}\) 放进去, 可以维护第一个
第二个简单线段树处理即可

总结

点对贡献维护

区间问题往往可以转化成点对问题

常见 $\rm{trick}$ : 点对贡献维护, 类似扫描线的思路, 一维枚举一维数据结构处理

注意形式化约束条件有时可以简化问题

原来这个时候已经开始数据检验了吗, 那还是进步挺小的