PERIODNI

思路

哇, 看到这个就直接想到昨天学的经典应用 : 最大子矩形

好吧还是认真推一下

完蛋了是计数, 我们没救了

首先按照高度为优先级, 位置为键值建一颗小根笛卡尔树, 我们玩下样例找下性质

例如题目中给出的图片, 我们建成笛卡尔树就长这样

其中每个点由 \(\{键值, 优先级\}\) 组成

观察这颗笛卡尔树, 我们看看有什么性质

容易发现每个点如果要放上数字, 那么一定只能放一个, 因为题目中明确说明 "不得有任意两个数在同一行或者同一列"

好吧不太会做, 我们去看下 \(\rm{TJ}\)

\(\rm{Part \ 1}\) : 笛卡尔树分割多边形

这里有一个前置知识, 也就是在规范的四边形中, 这个问题应当如何求解

那么我们想办法把这些多边形拆开方便计算, \(\rm{belike}\) :

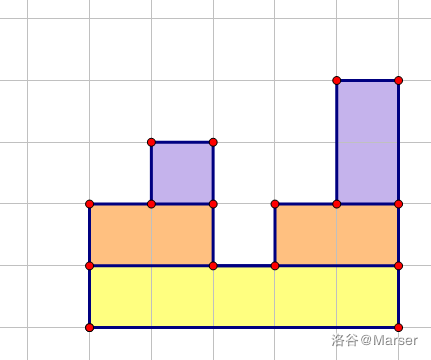
这样构成的若干个矩形正好满足笛卡尔树的性质:

\(\rm{tldraw}\) 好东西

你发现我们之前对 \(\{h_i\}\) 建树, 不刚好就长这样吗
具体的, 一定是 \(h_i\) 小的点更早被分割, 善哉, 完美符合要求
一个小问题是有可能有些情况会出现不能恰好分成二叉的情况, 但是你发现这种情况下可以将其二度化照样处理, \(\rm{belike}\) :

\[\Downarrow \]

在实现上, 你只需要把每次分割不全的部分合到一起丢下去下次在分开即可, 当然如果用笛卡尔树建那就不用管

注意对于笛卡尔树上的点, 我们都需要记录其长以及宽, 以下设为 \(L_i, H_i\)

时间复杂度 : \(\mathcal{O} (n)\)

\(\rm{Part \ 2}\) : 树上背包

有了以上的知识, 我们就可以把这个题转化成一个在树上做背包的计数类问题

具体怎么做? 先学一下树上背包

把 \(u\) 子树上的点看做一个组, 把 \(u\) 子树中所有点的最大取点和看做容量, 每个点看做物品, 体积为 \(1\) \(\cdots\)

其实个人认为不需要这么复杂, 树上依赖的背包问题, 仅仅只是把状态的一维定义成了当前的 "容量" , 也不用去刻意的套

令 \(f_{i, j}\) 表示 \(i\) 及 \(i\) 的子树中, 取了 \(j\) 个互不冲突的点的可能性, 记 \(i\) 的左儿子为 \(l\) , 右儿子为 \(r\)

显然的, 这相当于在笛卡尔树上进行树形 \(\rm{dp}\) , 由于其良好的二叉树性质, 还是很好处理的

找一个朴素的转移, 不难写出 (需要注意的是每个点互不相同, 题目没有明确表述)

\[f_{i, j} = \sum_{k = 0}^{j} \sum_{h = 0}^{j - h} f_{l, k} \cdot f_{r, h} \cdot {L_i - k - h \choose j - k - h} \cdot {H_i \choose j - k - h} \cdot {(j - k - h)}! \]

初始化每个叶子结点 \(i\) : \(f_{i, j} = {L_i \choose j} \cdot {H_i \choose j } \cdot j!\)

答案即为 \(f_{root, k}\)

你发现这样做是 \(\mathcal{O} (n k^3)\) 的, 考虑优化

我们预处理 \(\displaystyle g_{i, p} = \sum_{h + j = p} f_{l, j} \cdot f_{r, h}\) , 可以把上面的转移降到 \(\mathcal{O} (n k^2)\)

现在的柿子是

\[f_{i, j} = \sum_{p = 0}^{j} g_{i, p} \cdot {L_i - p \choose j - p} \cdot {h_i \choose j - p} \cdot (j - p)! \]

总时间复杂度 \(\mathcal{O} (nk^2)\)

实现

框架

首先根据 \(\{h_i\}\) 建树

关于如何记录 \(H, L\) :
你发现每一个点的 \(H\) 等于其高度减去其父亲高度
每一个点的 \(L\) 从其子节点递推过来即可

代码

#include <bits/stdc++.h>
const int MOD = 1e9 + 7;
#define int __int128
const int MAXN = 520; // 641
const int INF = 1e20;
const int MAXVAL = 1e6 + 20;
const int VAL = 1e6 + 15;

namespace IO
{
    inline int read() {
        int f = 1, x = 0;
        char ch = getchar();
        while (ch < '0' || ch > '9') {
            if (ch == '-') f = -1;
            ch = getchar();
        }
        while (ch >= '0' && ch <= '9')
            x = x * 10 + (ch - '0'), ch = getchar();
        return x * f;
    }

    void write(int x) {
        if (x < 0)
            putchar('-'), x = -x;
        if (x > 9)
            write(x / 10);
        putchar(x % 10 + '0');
        return;
    }

};
using namespace IO;

int n, k;
int h[MAXN];

long long fac[MAXVAL], ifac[MAXVAL];
int quickpow(int x, int p) {
	int ans = 1, base = x;
	while (p) {
		if (p & 1) ans = (ans * base) % MOD;
		base = (base * base) % MOD;
		p >>= 1;
	}
	return ans;
}

int mul(int a, int b) { return ((a % MOD) * (b % MOD) * 1ll) % MOD; }
int dec(int a, int b) { return (a + MOD - b) % MOD; }
int add(int a, int b) { return (a + b) % MOD; }
void addon(__int128 &a, int b) { a = add(a, b); }

int C(int a, int b) {
    if (a < b || a < 0 || b < 0) return 0;
    return fac[a] * ifac[b] % MOD * ifac[a - b] % MOD;
}

class Catesian_Tree {
private:
    struct node {
        int ls, rs, fa; // 位置信息
        int val, key; // 优先级 & 键值
        int H, L; // 行数 & 列数
    } Tree[MAXN];

    void init() {
        for (int i = 1; i <= n; i++) Tree[i].val = h[i], Tree[i].key = i;
        Tree[0].val = -INF, Tree[0].key = 0;
    }

    /*寻找笛卡尔树中的根节点*/
    int findroot() {
        bool vis[MAXN];
        for (int i = 1; i <= n; i++) vis[Tree[i].ls] = vis[Tree[i].rs] = true;
        for (int i = 1; i <= n; i++) if (!vis[i]) return i;
    }

    /*计算 H, L 的辅助函数*/
    void dfs1(int now, int fa) {
        /*计算 H*/
        if (~fa) Tree[now].H = Tree[now].val - Tree[fa].val;
        else Tree[now].H = Tree[now].val;
        
        if (Tree[now].ls) dfs1(Tree[now].ls, now);
        if (Tree[now].rs) dfs1(Tree[now].rs, now);
    }

    int f[MAXN][MAXN], g[MAXN][MAXN << 1];
    /*树形 dp 的辅助函数*/
    void dfs2(int now, int fa) {
        /*初始化*/
        if (!Tree[now].ls && !Tree[now].rs) {
            Tree[now].L = 1;
            for (int j = 0; j <= Tree[now].L; j++)
                f[now][j] = mul(mul(C(Tree[now].H, j), C(Tree[now].L, j)), fac[j]);
            return ;
        }

        if (Tree[now].ls) dfs2(Tree[now].ls, now);
        if (Tree[now].rs) dfs2(Tree[now].rs, now);
        Tree[now].L = Tree[Tree[now].ls].L + Tree[Tree[now].rs].L + 1;

        /*预处理 g*/
        for (int i = 0; i <= Tree[Tree[now].ls].L; i++)
            for (int j = 0; j <= Tree[Tree[now].rs].L; j++)
                addon(g[now][i + j], mul(f[Tree[now].ls][i], f[Tree[now].rs][j]));

        /*计算 f*/
        for (int j = 0; j <= Tree[now].L; j++)
            for (int p = 0; p <= j; p++)
                addon(f[now][j], mul(mul(g[now][p], C(Tree[now].H, j - p)), mul(C(Tree[now].L - p, j - p), fac[j - p])));
    }
public:
    /*建立笛卡尔树 (小根)*/
    void buildtree() {
        init();
        std::stack<int> MS; MS.push(0);
        for (int i = 1; i <= n; i++) {
            int pos = MS.top();
            while (!MS.empty() && Tree[pos].val > Tree[i].val) { pos = Tree[MS.top()].fa; MS.pop(); }
            Tree[i].ls = Tree[pos].rs, Tree[Tree[i].ls].fa = i, Tree[i].fa = pos, Tree[pos].rs = i;
            MS.push(i); //
        }
    }

    /*计算笛卡尔树中的 H, L*/
    void calcHL() {
        int root = findroot();
        Tree[root].L = n;
        dfs1(root, -1);
    }

    /*树形 dp*/
    void solve() {
        int root = findroot();
        memset(f, 0, sizeof(f)), memset(g, 0, sizeof(g));
        f[0][0] = 1;
        dfs2(root, -1);
        write(f[root][k] % MOD);
    }
} CT;

signed main() {
    n = read(), k = read();
    for (int i = 1; i <= n; i++) h[i] = read();

    fac[0] = 1;
    for (int i = 1; i <= VAL; i++) fac[i] = fac[i - 1] * i % MOD;
    ifac[VAL] = quickpow(fac[VAL], MOD - 2);
    for (int i = VAL - 1; ~i; i--) ifac[i] = ifac[i + 1] % MOD * (i + 1) % MOD;


    CT.buildtree();
    CT.calcHL();
    CT.solve();

    return 0;
}

不想调了, 毁灭吧

总结

笛卡尔树可以解决一类最大子矩阵问题

组合数学处理规则图形是方便的, 一般把多边形转化成规则图形

预处理可以降低 \(\rm{dp}\) 的复杂度

树上问题考虑类树形 \(\rm{dp}\) 的去做最保险

以后代码越短越好, 方便调试