[CSP-S 2021] 回文
算法
暴力
容易发现双指针可以找到每一个区间 \([L, R]\), 使得这个区间覆盖 \(1\) ~ \(n\) 的每一个数, 也即区间外覆盖 \(1\) ~ \(n\) 的每一个数, 这是 \(O(n)\) 的
考虑判断
对于两个数列 \(A\), \(B\)
显然, 在 \(A\) 中先取出的要在 \(B\) 中最后取出, 所以把 \(A\) 分两段压入栈中, 判断栈顶是否在 \(B\) 的两端出现, 完事之后记录一下
正解
发现瓶颈在 \(O(n)\) 找区间上
如果假设第一次取左端
那么与之相对应唯一确定的一个数就必须最后一个取
于是分成两段
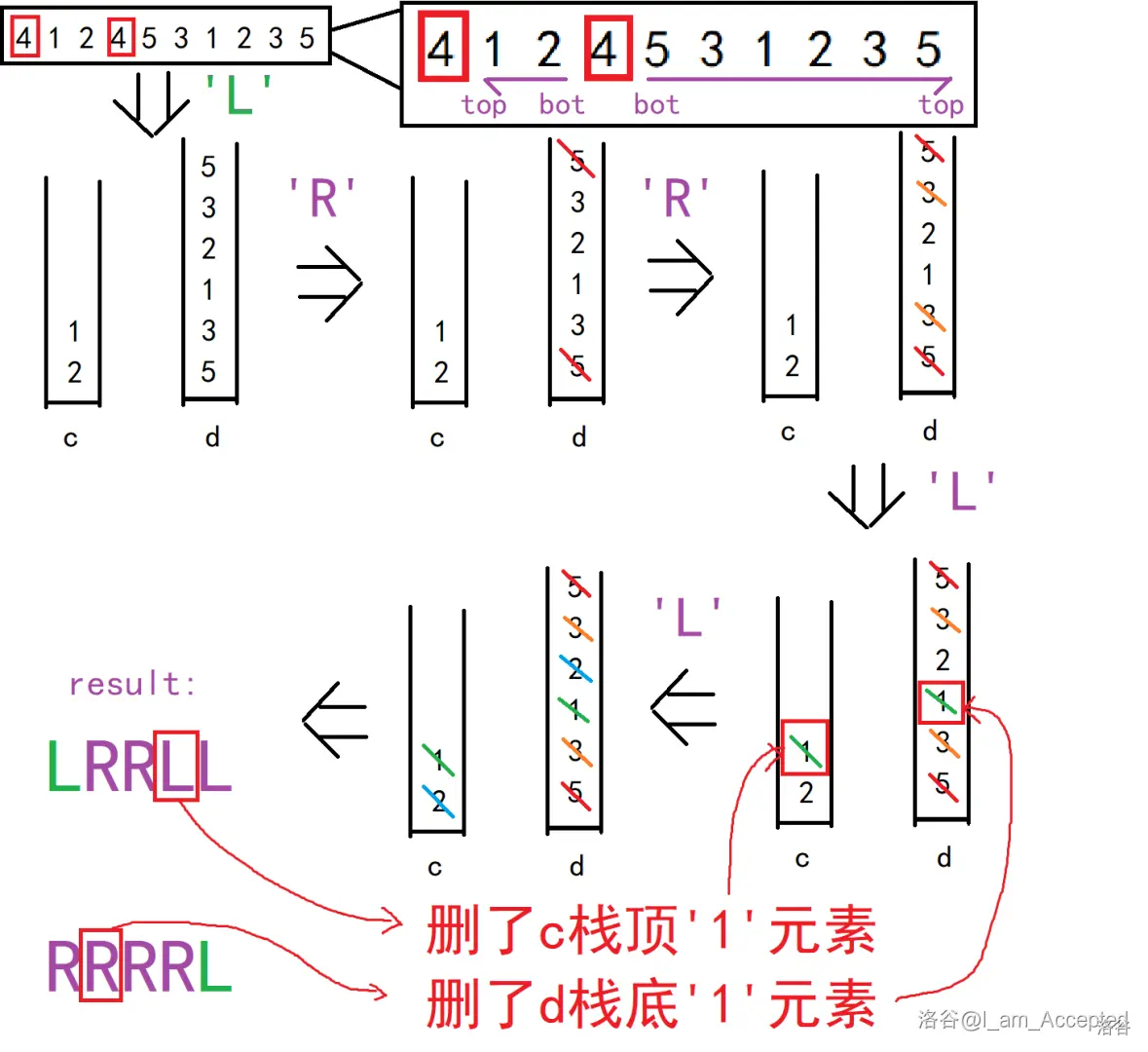
于是易得
代码
暴力代码
#include <bits/stdc++.h>
const int MAXN = 5e5 + 20;
int T;
int n;
int a[MAXN << 2];
/*手写栈*/
class stack
{
private:
public:
int Val[MAXN << 1];
int top_pos = 0;
void push(int x)
{
Val[++top_pos] = x;
}
bool empty()
{
return top_pos == 0;
}
void pop()
{
top_pos--;
}
int top()
{
return Val[top_pos];
}
} Left_Part, Right_Part;
/*暴力*/
char Ans[MAXN]; //
char Now[MAXN]; //
int Appeared[MAXN << 1];
int Appeared_Num = 0;
void Appeared_init();
bool check();
void clear();
bool Have_Ans = false; //
bool Have_Now = false; //
void Brute_check_ans(int Left, int Right)
{
Have_Now = true;
clear();
for (int i = 1; i < Left; i++)
Left_Part.push(a[i]);
for (int i = 2 * n; i > Right; i--) //
Right_Part.push(a[i]);
int Mid_Part_Left = Left;
int Mid_Part_Right = Right;
int Input_Time = 0;
memset(Now, 0, sizeof(Now));
while(Mid_Part_Left <= Mid_Part_Right)
{
/*注意判断顺序*/
if (Right_Part.top() == a[Mid_Part_Left])
{
Right_Part.pop();
Now[n - Input_Time] = 'R';
Now[n + Input_Time + 1] = 'L';
Input_Time++;
Mid_Part_Left++;
}else if (Right_Part.top() == a[Mid_Part_Right])
{
Right_Part.pop();
Now[n - Input_Time] = 'R';
Now[n + Input_Time + 1] = 'R';
Input_Time++;
Mid_Part_Right--;
}
else if (Left_Part.top() == a[Mid_Part_Left])
{
Left_Part.pop();
Now[n - Input_Time] = 'L';
Now[n + Input_Time + 1] = 'L';
Input_Time++;
Mid_Part_Left++;
}else if (Left_Part.top() == a[Mid_Part_Right])
{
Left_Part.pop();
Now[n - Input_Time] = 'L';
Now[n + Input_Time + 1] = 'R';
Input_Time++;
Mid_Part_Right--;
}
else{
Have_Now = false;
memset(Now, 0, sizeof(Now));
clear();
return;
}
}
if(Have_Ans && Have_Now)
{
/*Ans 检查*/
bool flag = false;
for (int i = 1; i <= 2 * n; i++)
{
if (Ans[i] != Now[i])
{
if (Ans[i] < Now[i])
{
flag = false;
break;
}
else
{
flag = true;
break;
}
}
}
if (flag)
{
for (int i = 1; i <= 2 * n; i++)
{
Ans[i] = Now[i];
}
}
}else if(Have_Now){
for (int i = 1; i <= 2 * n; i++)
{
Ans[i] = Now[i];
}
Have_Ans = true;
}
clear();
return;
}
void solve1()
{
Appeared_init();
int Left, Right;
for (Left = 1; Left <= n + 1; Left++)
{
Right = Left + n - 1;
if(Left != 1)
{
if (--Appeared[a[Left - 1]] == 0)
Appeared_Num--;
if (Appeared[a[Right]]++ == 0)
Appeared_Num++;
}
if(check())
{
//printf("%d %d\n", Left, Right);
Brute_check_ans(Left, Right);
//std::cout << Ans << '\n';
}
}
}
int main()
{
scanf("%d", &T);
while(T--)
{
scanf("%d", &n);
for (int i = 1; i <= n * 2; i++)
{
scanf("%d", &a[i]);
}
solve1();
if(!Have_Ans)
{
printf("-1\n");
}else{
for (int i = 1; i <= n * 2; i++)
{
std::cout << Ans[i];
}
printf("\n");
}
}
return 0;
}
bool check()
{
return Appeared_Num == n;
}
void Appeared_init()
{
Have_Ans = false;
memset(Ans, 0, sizeof(Ans));
memset(Appeared, 0, sizeof(Appeared));
Appeared_Num = 0;
for (int i = 1; i <= n; i++)
{
Appeared_Num += (Appeared[a[i]] != 0) ? 0 : 1;
Appeared[a[i]]++;
}
}
void clear()
{
while(!Left_Part.empty())
Left_Part.pop();
while(!Right_Part.empty())
Right_Part.pop();
}
/*
2
5
4 1 2 4 5 3 1 2 3 5
3
3 2 1 2 1 3
LRRLLRRRRL
-1
*/
正解代码
#include<cstdio>
int n;
char res[1000005];
int a[1000005];
inline int read() {
register int x=0,f=1;register char s=getchar();
while(s>'9'||s<'0') {if(s=='-') f=-1;s=getchar();}
while(s>='0'&&s<='9') {x=x*10+s-'0';s=getchar();}
return x*f;
}
inline bool work(int l1,int r1,int l2,int r2) {
for(register int i=1;i<n;++i) {
if(l1<=r1&&((l2<=r2&&a[l1]==a[l2])||(l1<r1&&a[l1]==a[r1]))) {
if(l1<r1&&a[l1]==a[r1]) {
++l1; --r1;
res[i]='L'; res[2*(n-1)-i+1]='L';
}
else {
++l1; ++l2;
res[i]='L'; res[2*(n-1)-i+1]='R';
}
}
else if(l2<=r2&&((l1<=r1&&a[r2]==a[r1])||(l2<r2&&a[l2]==a[r2]))) {
if(l2<r2&&a[l2]==a[r2]) {
++l2; --r2;
res[i]='R'; res[2*(n-1)-i+1]='R';
}
else {
--r2; --r1;
res[i]='R'; res[2*(n-1)-i+1]='L';
}
}
else {return 0;}
}
return 1;
}
int main() {
int T=read();
while(T--) {
n=read();int p1=-1,p2=-1;
for(register int i=1;i<=2*n;++i) a[i]=read();
for(register int i=1;i<=2*n+1;++i) res[i]=0;
for(register int i=2;i<=2*n;++i) {if(a[1]==a[i]) {p1=i; break;}}
for(register int i=1;i<2*n;++i) {if(a[2*n]==a[i]) {p2=i; break;}}
if(work(2,p1-1,p1+1,2*n)) {printf("L%sL\n",res+1);}
else if(work(1,p2-1,p2+1,2*n-1)) {printf("R%sL\n",res+1);}
else {printf("-1\n");}
}
return 0;
}
总结
思路
善于运用基础数据结构
分析瓶颈之后想办法优化
逆向思维, 正向不好思考时转化一下
也可以利用特殊样例口胡(不建议, 容易被特殊性质诈骗)
注意最优解的顺序, 由于填答案的顺序不是正向, 所以要特殊顺序
代码
注意 STL 效率
注意初始化
注意 string 不能直接赋值
注意思路复现
