8月10总结
CYJian的糖果解题报告
题目如下:
他现在有$n$大块糖果 ,每大块糖果有$r[i]-l[i]+1$小块糖果 ,每小块糖果的甜蜜度为l[i],l[i]+1,l[i]+2......r[i]。
现在他可以从每块大糖果中任选一块小糖果来组成他的糖果拼盘 ,设选出来的糖果的甜蜜度为x[1],x[2].....x[n] ,设![]() 。
。
定义这个糖果拼盘的幸福指数为![]() 。
。
现在CYJian要问你 ,他选出的拼盘的所有方案的幸福指数之和为多少?(输出答案对1e9+7取模的结果)
输入第一行一个正整数n ,表示大块糖果数量
接下来n行 ,每行一个l[i],r[i],输出一个数为答案。
样例输入1: 3 1 1 2 3 1 1 样例输出1: 13
样例输入2: 3 2 5 2 4 2 5 样例输出2: 282
PS: ![]() 表示
表示
ans=1; for(int i=1;i<=n;i++) ans*=(h-x[i]+1);
数学题????
老师上课推了两个小时的公式hhhh
简而言之就是将最大数(即h)相同的分为同一类
且在一个分类中必须含有1,若不含1则不符合题意(因为最大值减去自己+1为1)
例:
若共有两颗大糖果,且小糖果均为1,2,3
那么若所有点相连,共含9种情况,其中仅5种符合题意
在计算过程中用所有情况减去不符合的情况更好算
如图(标红为符合题意):
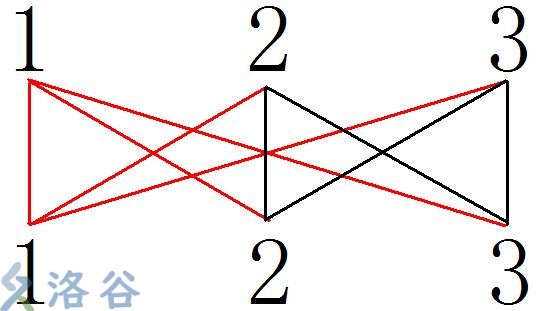
即运算为(伪):sum([1,3])-sum([2,3])。
再将每种最大值不同的情况相加%mod即可
要点!
由于题目要求为累乘,所以答案可能会非常大(题目中要求%1000000007老师说是出题人为了不让我们写高精)
普通来说,在加减乘的过程中一边(ans%mod+mod)%mod是不会有问题的
但是在除法中若变运算变除会导致答案错误,因此在写题过程中格外注意
Code:
1 #include<bits/stdc++.h> 2 #define mod 1000000007 3 #define Freopen(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);} 4 using namespace std; 5 int n; 6 long long Maxl,Maxr,ans; 7 long long l[1005],r[1005];//不开longlong见zs 8 long long solve(long long a1,long long a2){ 9 long long ret=1;//由于是累乘,所以要初始化为1 10 for(int i=1;i<=n;i++){//n个大糖果 11 long long rr=min(r[i],a1);//找出最大值,即h 12 long long sum=(rr-l[i]+1)%mod*(l[i]+rr)/2%mod;//除和%的部分要格外注意 13 //到这里sum=x[1]+x[2]+...x[n] (首项加末项乘项数除以2) 14 sum=(((rr-l[i]+1)%mod*(a2+1)%mod-sum)%mod+mod)%mod; 15 //到这里sum=本次挑选的糖果甜蜜度的累乘 16 ret=(ret*sum)%mod; 17 } 18 return ret; 19 } 20 int main(){ 21 Freopen(a); 22 scanf("%d",&n); 23 for(int i=1;i<=n;i++){ 24 scanf("%d%d",&l[i],&r[i]); 25 Maxl=max(Maxl,l[i]),Maxr=max(Maxr,r[i]);//找出r,l中的最大值 26 } 27 for(int i=Maxl;i<=Maxr;i++){ 28 long long tmp=((solve(i,i)-solve(i-1,i))%mod+mod)%mod;//对不同的情况进行运算 29 //solve(i,i)相当于例中的sum([1,3]),solve(i-1,i)相当于例中的sum([2,3]) 30 ans=(ans+tmp)%mod; 31 } 32 printf("%lld",ans); 33 return 0; 34 }
总结:看代码其实挺简单的
但是对于这样的数学性强的题,重点在于自己能不能想到8反正我是没想到
其实上面的东西都是老师上课分析的hhhh雨我无瓜


 浙公网安备 33010602011771号
浙公网安备 33010602011771号