关于Hall定理的学习

基本定义

\(Hall\) 定理是二分图匹配的相关定理
用于判断二分图是否存在完美匹配
存在完美匹配的二分图即满足最大匹配数为 \(min(|X|,|Y|)\) 的二分图,也就是至少有一边的点全部被匹配到了

定理

设 \(M(U)\) 为与 \(U\) 中的点相连的点集，一个二分图 \(U,V(|U|<=|V|)\) 存在完美匹配，满足对于任意点集 \(x∈U\) 都有 \(|M(X)|>=|X|\)

必要性证明

连出去的边数都不足点数,那么显然不能构成完美匹配

充分性证明

假如存在一个满足 \(Hall\) 定理的二分图 , 且不满足完美匹配
那么假设两边都存在一个未匹配的点 , 由于满足 \(Hall\) 定理 , 这个没有被匹配的点肯定有一条没有被匹配的边
那么假设这条边对面的点被匹配过了 , 这个点和那个未匹配的点组成 \(|X|\) 后, 这个点又一定连向了除它匹配的点外的至少一个点
这样下去就一定可以找到这条增广路了 , 所以一定是可以满足完美匹配的

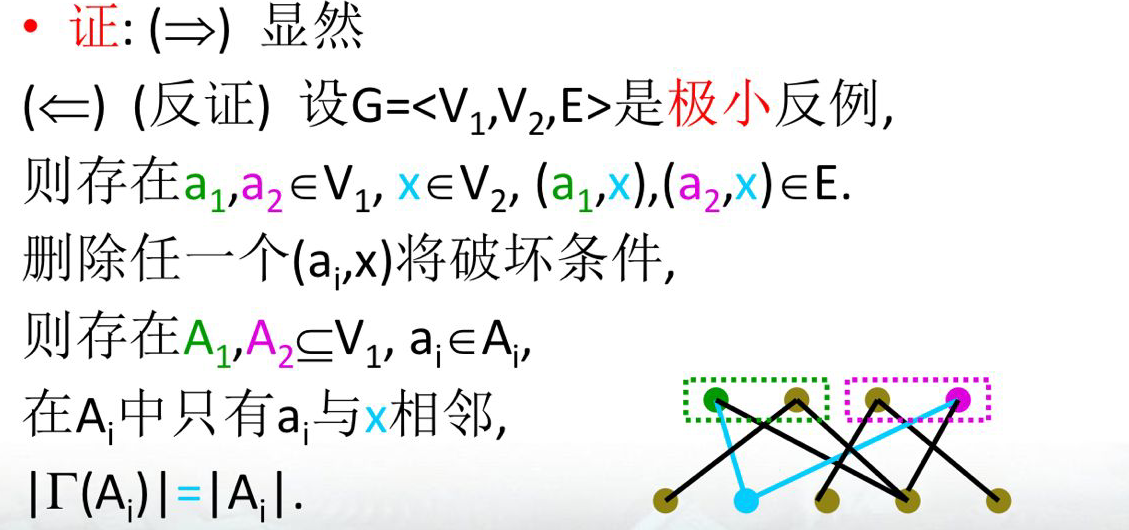
upd(2021):

由于之前的证明有些意识流，且访问量有点高，决定把书上的严格证明贴出来，供大家参考(偷懒)。