bzoj 3218: a + b Problem
Description
.jpg)
.jpg)
Input
Output
Sample Input
10
0 1 7 3 9 2
7 4 0 9 10 5
1 0 4 2 10 2
7 9 1 5 7 2
6 3 5 3 6 2
6 6 4 1 8 1
6 1 6 0 6 5
2 2 5 0 9 3
5 1 3 0 2 5
5 6 7 1 1 2
0 1 7 3 9 2
7 4 0 9 10 5
1 0 4 2 10 2
7 9 1 5 7 2
6 3 5 3 6 2
6 6 4 1 8 1
6 1 6 0 6 5
2 2 5 0 9 3
5 1 3 0 2 5
5 6 7 1 1 2
Sample Output
55
题解:
这题要好好总结,真是抓狂的A+B problem.
首先非常容易想到O(n^2)空间复杂度的网络流建图,和为了博多一题类似(SUM-不合法),区别在于中间那条双向边改成单向边.
因为一个点只有一次被认为是奇怪方格的机会,所以拆点(i',i,p[i]),限制p[i],所以枚举前i个点,满足条件就连边到i'
综上:
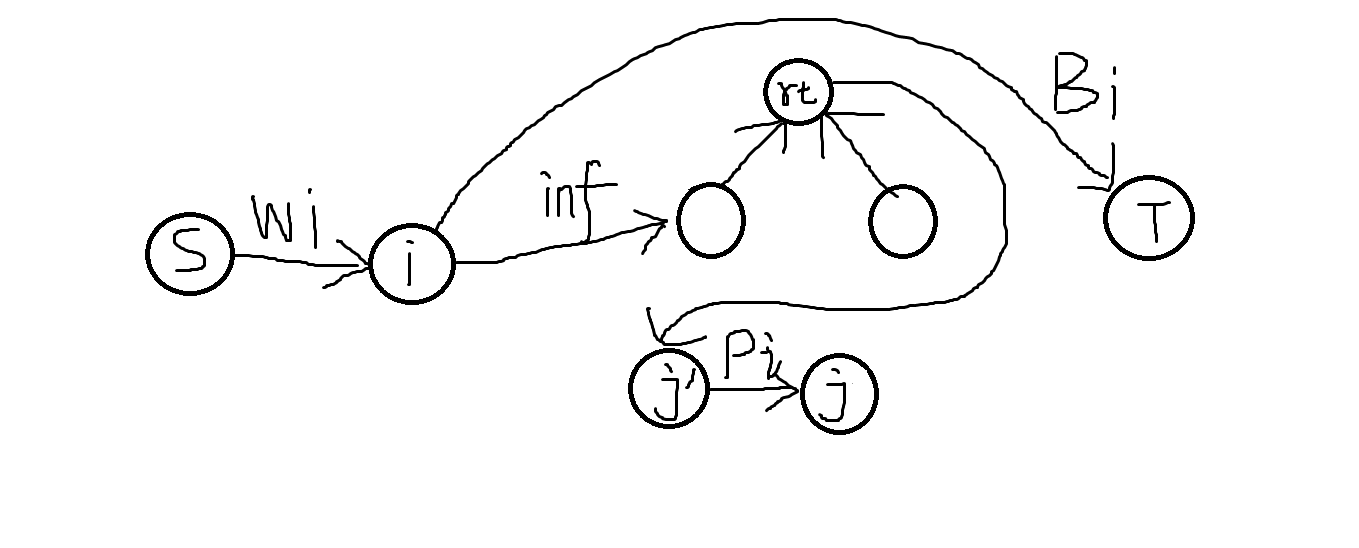
连(S,i,w[i])(i,T,b[i])(i',i,p[i]) 如果满足条件的j (j,i',inf)
这样空间显然不允许,然后就来了奇怪的主席树上跑网络流,直接建好树以后把(j,i',inf)改成j连主席树上的点即可
被i覆盖的区间我们就在主席树上向j’连边 大致图如下 对所有点都做相同处理:
HINT:
1.傻逼错误:为了省内存num初值设为-1....然后for里没改.
2.很重要的地方:i连向的旧节点要对新节点建边,不然在主席树上无法流通

1 #include <algorithm> 2 #include <iostream> 3 #include <cstdlib> 4 #include <cstring> 5 #include <cstdio> 6 #include <cmath> 7 using namespace std; 8 const int N=12333,M=3200005,inf=2e9; 9 typedef long long ll; 10 int head[N],num=-1; 11 struct Lin{ 12 int next,to,dis; 13 }a[M]; 14 int gi(){ 15 int str=0;char ch=getchar(); 16 while(ch>'9' || ch<'0')ch=getchar(); 17 while(ch>='0' && ch<='9')str=(str<<1)+(str<<3)+ch-48,ch=getchar(); 18 return str; 19 } 20 void init(int x,int y,int dis){ 21 a[++num].next=head[x];a[num].to=y;a[num].dis=dis;head[x]=num; 22 } 23 void addedge(int x,int y,int dis){ 24 init(x,y,dis);init(y,x,0); 25 } 26 int n,s[N],q[N],b[N],w[N],l[N],r[N],p[N],S=0,T,dep[N]; 27 bool bfs(){ 28 memset(dep,0,sizeof(dep)); 29 int u,x,t=0,sum=1; 30 q[1]=S;dep[S]=1; 31 while(t!=sum){ 32 x=q[++t]; 33 for(int i=head[x];i;i=a[i].next){ 34 u=a[i].to; 35 if(dep[u] || a[i].dis<=0)continue; 36 dep[u]=dep[x]+1;q[++sum]=u; 37 } 38 } 39 return dep[T]; 40 } 41 int dfs(int x,int flow){ 42 if(!flow || x==T)return flow; 43 int tmp,tot=0,u; 44 for(int i=head[x];i;i=a[i].next){ 45 u=a[i].to; 46 if(dep[u]!=dep[x]+1 || a[i].dis<=0)continue; 47 tmp=dfs(u,min(flow,a[i].dis)); 48 a[i].dis-=tmp;a[i^1].dis+=tmp; 49 tot+=tmp;flow-=tmp; 50 if(!flow)break; 51 } 52 if(!tot)dep[x]=0; 53 return tot; 54 } 55 int maxflow(){ 56 int tot=0,tmp; 57 while(bfs()){ 58 tmp=dfs(S,inf); 59 while(tmp)tot+=tmp,tmp=dfs(S,inf); 60 } 61 return tot; 62 } 63 void work(){ 64 n=gi();T=2*n+1;ll ans=0; 65 for(int i=1;i<=n;i++){ 66 s[i]=gi();b[i]=gi();w[i]=gi();l[i]=gi();r[i]=gi();p[i]=gi(); 67 ans+=b[i]+w[i]; 68 } 69 for(int i=1;i<=n;i++){ 70 addedge(S,i,w[i]);addedge(i,T,b[i]);addedge(i+n,i,p[i]); 71 for(int j=1;j<i;j++){ 72 if(l[i]<=s[j] && s[j]<=r[i])addedge(j,i+n,p[i]); 73 } 74 } 75 ans=ans-maxflow(); 76 printf("%lld\n",ans); 77 } 78 int main() 79 { 80 freopen("pp.in","r",stdin); 81 work(); 82 return 0; 83 }

1 #include <algorithm> 2 #include <iostream> 3 #include <cstdlib> 4 #include <cstring> 5 #include <cstdio> 6 #include <cmath> 7 using namespace std; 8 const int N=303333,M=820005,inf=2e9; 9 typedef long long ll; 10 int head[N],num=1,cnt=0,lim=0; 11 struct Lin{ 12 int next,to,dis; 13 }a[M]; 14 int gi(){ 15 int str=0;char ch=getchar(); 16 while(ch>'9' || ch<'0')ch=getchar(); 17 while(ch>='0' && ch<='9')str=(str<<1)+(str<<3)+ch-48,ch=getchar(); 18 return str; 19 } 20 void init(int x,int y,int dis){ 21 a[++num].next=head[x];a[num].to=y;a[num].dis=dis;head[x]=num; 22 } 23 void addedge(int x,int y,int dis){ 24 init(x,y,dis);init(y,x,0); 25 } 26 int n,s[N],q[N],b[N],w[N],L[N],R[N],p[N],S=0,T,dep[N]; 27 bool bfs(){ 28 memset(dep,0,sizeof(dep)); 29 int u,x,t=0,sum=1; 30 q[1]=S;dep[S]=1; 31 while(t!=sum){ 32 x=q[++t]; 33 for(int i=head[x];i;i=a[i].next){ 34 u=a[i].to; 35 if(dep[u] || a[i].dis<=0)continue; 36 dep[u]=dep[x]+1;q[++sum]=u; 37 } 38 } 39 return dep[T]; 40 } 41 int dfs(int x,int flow){ 42 if(!flow || x==T)return flow; 43 int tmp,tot=0,u; 44 for(int i=head[x];i;i=a[i].next){ 45 u=a[i].to; 46 if(dep[u]!=dep[x]+1 || a[i].dis<=0)continue; 47 tmp=dfs(u,min(flow,a[i].dis)); 48 a[i].dis-=tmp;a[i^1].dis+=tmp; 49 tot+=tmp;flow-=tmp; 50 if(!flow)break; 51 } 52 if(!tot)dep[x]=0; 53 return tot; 54 } 55 int maxflow(){ 56 int tot=0,tmp; 57 while(bfs()){ 58 tmp=dfs(S,inf); 59 while(tmp)tot+=tmp,tmp=dfs(S,inf); 60 } 61 return tot; 62 } 63 struct Segtree{ 64 int ls,rs; 65 }Tree[N<<1]; 66 int root[N]; 67 void updata(int &rt,int last,int l,int r,int ask,int id){ 68 rt=++cnt;Tree[rt]=Tree[last]; 69 if(l==r){ 70 addedge(id,rt+T,inf); 71 if(last)addedge(last+T,rt+T,inf); 72 return ; 73 } 74 int mid=(l+r)>>1; 75 if(ask<=mid)updata(Tree[rt].ls,Tree[last].ls,l,mid,ask,id); 76 else updata(Tree[rt].rs,Tree[last].rs,mid+1,r,ask,id); 77 if(Tree[rt].ls)addedge(Tree[rt].ls+T,rt+T,inf);if(Tree[rt].rs)addedge(Tree[rt].rs+T,rt+T,inf); 78 } 79 void query(int rt,int l,int r,int sa,int se,int id){ 80 if(!rt)return ; 81 if(sa<=l && r<=se){ 82 addedge(rt+T,id+n,inf); 83 return ; 84 } 85 int mid=(l+r)>>1; 86 if(sa<=mid)query(Tree[rt].ls,l,mid,sa,se,id); 87 if(se>mid)query(Tree[rt].rs,mid+1,r,sa,se,id); 88 } 89 void build(){ 90 for(int i=1;i<=n;i++){ 91 addedge(S,i,w[i]);addedge(i+n,i,p[i]);addedge(i,T,b[i]); 92 if(i>1)query(root[i-1],0,lim,L[i],R[i],i); 93 updata(root[i],root[i-1],0,lim,s[i],i); 94 } 95 } 96 void work(){ 97 n=gi();T=2*n+1;ll ans=0; 98 for(int i=1;i<=n;i++){ 99 s[i]=gi();b[i]=gi();w[i]=gi();L[i]=gi();R[i]=gi();p[i]=gi(); 100 if(R[i]>lim)lim=R[i];if(L[i]>lim)lim=L[i];if(s[i]>lim)lim=s[i]; 101 ans+=b[i]+w[i]; 102 } 103 build(); 104 ans=ans-maxflow(); 105 printf("%lld\n",ans); 106 } 107 int main() 108 { 109 //freopen("pp.in","r",stdin); 110 work(); 111 return 0; 112 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号