[ZJOI2006]物流运输 SPFA+DP

题目描述

物流公司要把一批货物从码头A运到码头B。由于货物量比较大，需要n天才能运完。货物运输过程中一般要转停好几个码头。物流公司通常会设计一条固定的运输路线，以便对整个运输过程实施严格的管理和跟踪。由于各种因素的存在，有的时候某个码头会无法装卸货物。这时候就必须修改运输路线，让货物能够按时到达目的地。但是修改路线是—件十分麻烦的事情，会带来额外的成本。因此物流公司希望能够订一个n天的运输计划，使得总成本尽可能地小。

输入输出格式

输入格式：

 

第一行是四个整数n(l≤n≤100)、m(l≤m≤20)、K和e。n表示货物运输所需天数，m表示码头总数，K表示每次修改运输路线所需成本。接下来e行每行是一条航线描述，包括了三个整数，依次表示航线连接的两个码头编号以及航线长度(>0)。其中码头A编号为1，码头B编号为m。单位长度的运输费用为1。航线是双向的。再接下来一行是一个整数d，后面的d行每行是三个整数P(1<P<m)，a，b(1≤a≤b≤n)。表示编号为P的码头从第a天到第b天无法装卸货物（含头尾）。同一个码头有可能在多个时间段内不可用。但任何时间都存在至少一条从码头A到码头B的运输路线。

 

输出格式：

 

包括了一个整数表示最小的总成本。总成本=n天运输路线长度之和+K*改变运输路线的次数。

 

输入输出样例

输入样例#1：
  5 5 10 8
  1 2 1
  1 3 3
  1 4 2
  2 3 2
  2 4 4
  3 4 1
  3 5 2
  4 5 2
  4
  2 2 3
  3 1 1
  3 3 3
  4 4 5
输出样例#1：
32

说明

【样例输入说明】

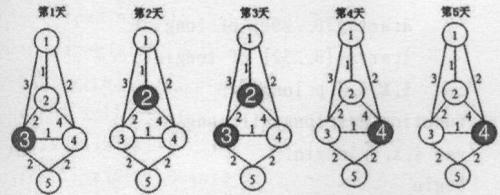
上图依次表示第1至第5天的情况，阴影表示不可用的码头。

【样例输出说明】

前三天走1-4-5，后两天走1-3-5，这样总成本为(2+2)*3+(3+2)*2+10=32。

题解：

我们先预处理出从[L,R]这几天中&&在满足某些点不能走的情况下的最短路，记为C[N][N];

于是可以进行DP：

设F[I]为前i天的最小总成本，可以得出： F[i]=min(F[i],F[j]+c[j+1][i]*(i-j)+k) k为改变线路所需的费用，（i-j）为这一段时间内的天数

具体看代码:

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 #include<cmath>
 6 #include<cstdlib>
 7 #include<ctime>
 8 #include<queue>
 9 using namespace std;
10 typedef long long ll;
11 const int N=105,M=1000005;
12 int n,m,k,day;
13 int gi()
14 {
15     int str=0;bool f=1;char ch=getchar();
16     while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
17     while(ch>='0' && ch<='9')str=str*10+ch-'0',ch=getchar();
18     return str*f;
19 }
20 const int INF=1999999999;
21 struct Lin
22 {
23     int next,to,dis;
24 }a[N*N*2];
25 bool vis[N];
26 int head[N],num=0;int c[N][N],f[N];
27 bool nort[21];
28 bool d[21][N];
29 int F[N];
30 void spfa(int from,int to)//表示从第from天到to天 
31 {
32     int x,u;
33     queue<int>q;
34     q.push(1);
35     for(int i=1;i<=n;i++)f[i]=INF,vis[i]=false;
36     vis[1]=true;f[1]=0;
37     while(!q.empty())
38     {
39         x=q.front();q.pop();
40         for(int i=head[x];i;i=a[i].next){
41             u=a[i].to;
42             if(!nort[u]){//如果该点在from-to中不能通行则不能加入队列 
43                 if(f[x]+a[i].dis<f[u]){
44                     f[u]=f[x]+a[i].dis;
45                      if(!vis[u]){
46                         vis[u]=true;q.push(u);
47                     }
48                 }
49             }
50         }
51         vis[x]=false;
52     }
53     c[from][to]=f[n];
54 }
55 void init(int x,int y,int z)
56 {
57     a[++num].next=head[x];
58     a[num].to=y;
59     a[num].dis=z;
60     head[x]=num;
61 }
62 int main()
63 {
64     int x,y,z;
65     day=gi();n=gi();k=gi();m=gi();
66     for(int i=1;i<=m;i++){
67         x=gi();y=gi();z=gi();
68         init(x,y,z);init(y,x,z);
69     }
70     int ppap=gi(),ls,rs;
71     for(int i=1;i<=ppap;i++){
72         x=gi();ls=gi();rs=gi();
73         for(int j=ls;j<=rs;j++)d[x][j]=true;
74     }
75     for(int i=1;i<=day;i++){//预处理 
76         memset(nort,0,sizeof(nort));
77         for(int j=i;j<=day;j++){
78             for(int k=1;k<=n;k++)nort[k]|=d[k][j];
79             spfa(i,j);
80         }
81     }
82     memset(F,127/3,sizeof(F));
83     F[0]=-k;
84     for(int i=1;i<=day;i++){
85         for(int j=0;j<=i-1;j++)
86         if(c[j+1][i]!=INF)
87         F[i]=min(F[i],F[j]+c[j+1][i]*(i-j)+k);
88     }
89     printf("%d",F[day]);
90     return 0;
91 }

 

posted @ 2017-05-02 14:53  PIPIBoss  阅读(236)  评论(0)  编辑  收藏  举报