「AcWing学习记录」背包问题

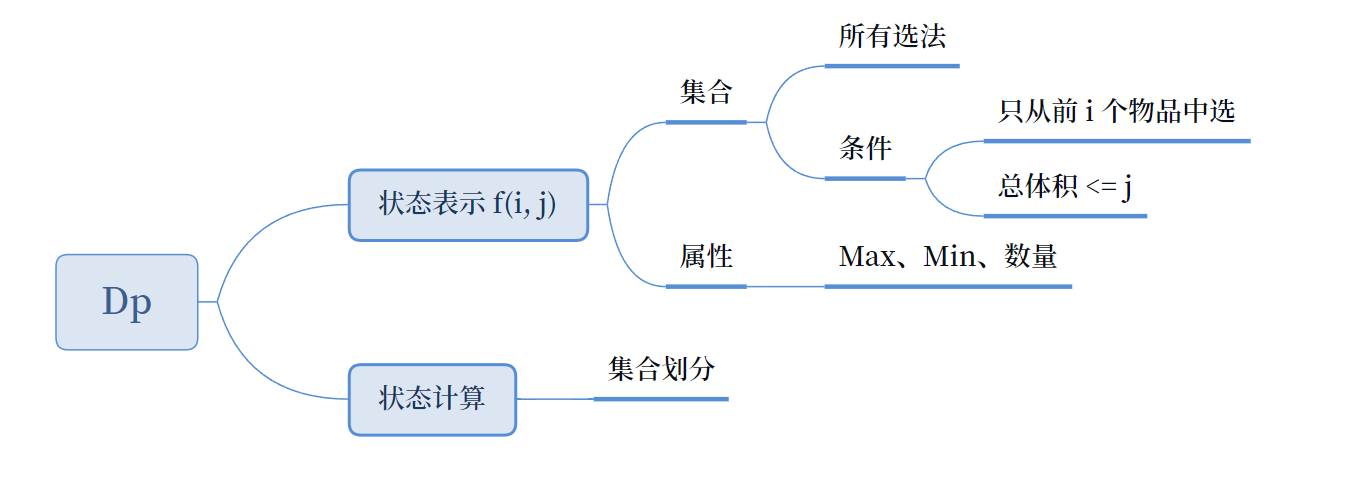
集合划分一般需要满足不重和不漏两个条件，不漏是一定要满足的，但不重不一定任何时候都要满足。

AcWing 2. 01背包问题

原题链接

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

数据范围
0 < N, V ≤ 1000
0 < vi, wi ≤ 1000

集合划分

\[f[i, j] = max(f[i-1, j], f[i-1, j-vi] + wi) \]

//二维形式
#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{
    cin >> n >> m;

    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];

/*循环若改为
for(int i = 1; i <= n; i++)
    for(int j = v[i]; j <= m; j++)
        f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
当v[i] > v[i + 1]时，如果f[i - 1][j]之前变更过，
那么f[i][j]则不会更新，会在下一次的f[i][j - v[i + 1]]中出现问题*/

    for(int i = 1; i <= n; i++)
    {
        for(int j = 0; j <= m; j++) //j从0而不从1开始循环的必要性在于存在v[i] = 0的特殊情况
        {
            f[i][j] = f[i - 1][j]; //这句的必要性在于一维本身表示的是上一层的值，而二维需要实时更新
            if(j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
        }
    }
    cout << f[n][m] << endl;

    return 0;
}

/*f(i) 只用到了 f(i-1)，并且 j 和 j-vi 都是小于等于 j 的，可以用滚动数组来优化*/

//一维形式（01背包问题的终极写法）
#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;

    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i++)
        for(int j = m; j >= v[i]; j--)
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;

    return 0;
}

AcWing 3. 完全背包问题

原题链接

有 N 种物品和一个容量是 V 的背包，每种物品都有无限件可用。

第 i 种物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

数据范围
0 < N, V ≤ 1000
0 < vi, wi ≤ 1000

集合划分

\[f[i, j] = \max_{0 \leq k \leq V/vi} f[i-1, j-vi* k] + wi* k \]

//二维形式
#include<iostream>
#include<algorithm>

using namespace std;

const int N =1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    for(int i = 1 ; i <= n; i++) cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i++)
        for(int j = 0; j <= m; j++)
            for(int k = 0; k * v[i] <= j; k++) //当k = 0时本身实现了f[i][j] = f[i - 1][j]的赋值
                f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);

    cout << f[n][m] << endl;

    return 0;
}

/*f[i, j]   = max(f[i-1, j], f[i-1, j-v]+w, f[i-1, j-2v]+2w, f[i-1, j-3v]+3w, …) = max(f[i-1, j], f[i, j-v]+w)
  f[i, j-v] = max(           f[i-1, j-v]  , f[i-1, j-2v]+ w, f[i-1, j-3v]+2w, …)*/

//一维形式
#include<iostream>
#include<algorithm>

using namespace std;

const int N =1010;

int n, m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;
    for(int i = 1 ; i <= n; i++) cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i++)
        for(int j = v[i]; j <= m; j++)
                f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;

    return 0;
}

01背包与完全背包的区别
\(f[i, j] = max(f[i-1, j], f[i-1, j-v]+w)\)
\(f[i, j] = max(f[i-1, j], f[i, j-v]+w)\)
一维形式的代码仅有逆序和正序循环的差别

AcWing 4. 多重背包问题

原题链接

有 N 种物品和一个容量是 V 的背包。

第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

数据范围
0 < N, V ≤ 100
0 < vi, wi, si ≤ 100

集合划分

\[f[i, j] = \max_{0 \leq k \leq si} f[i-1, j-vi* k] + wi* k \]

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 110;

int n, m;
int v[N], w[N], s[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];

    for(int i = 1; i <= n; i++)
        for(int j = 0; j <= m; j++)
            for(int k = 0; k <= s[i] && k * v[i] <= j; k++)
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);

    cout << f[n][m] << endl;
    return 0;
}

AcWing 5. 多重背包问题 II

原题链接

有 N 种物品和一个容量是 V 的背包。

第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

数据范围
0 < N ≤ 1000
0 < V ≤ 2000
0 < vi, wi, si ≤ 2000

/*f[i, j]   = max(f[i-1, j], f[i-1, j-v]+w, f[i-1, j-2v]+2w, …, f[i-1, j-sv]+sw)
  f[i, j-v] = max(           f[i-1, j-v]  , f[i-1, j-2v]+ w, …, f[i-1, j-(s+1)v]+sw)
由于max可以做加法，但不可以做减法，所以不能用完全背包问题的优化方式来优化多重背包问题，或者说不能直接用该优化方式来优化

二进制的优化方法(logn)
假设s = 1 + 2 + 4 + 8 + … + 2^k + c (c <= 2^{k+1})，可以把s以此方式分为若干组，并且可以拼凑出0-s之间的任意组合，即枚举若干个新的物品选和不选，就可以拼凑出第i个物品的所有方案
多重背包问题就转化成了01背包问题
时间复杂度从之前的NVs缩减至NVlogs
*/

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 12000;

int n, m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;

    int cnt = 0;
    for(int i = 0; i < n; i++)
    {
        int a, b, s;
        cin >> a >> b >> s;
        int k = 1;
        while(k <= s)
        {
            cnt++;
            v[cnt] = a * k;
            w[cnt] = b * k;
            s -= k;
            k *= 2;
        }
        if(s > 0)
        {
            cnt++;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }
    }
    n = cnt;

    for(int i = 1; i <= n; i++)
        for(int j = m; j >= v[i]; j--)
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;
    return 0;
}

AcWing 9. 分组背包问题

原题链接

有 N 组物品和一个容量是 V 的背包。

第 i 组物品有 Si 个，同一组内的物品最多只能选一个。
每件物品的体积是 vij，价值是 wij，其中 i 是组号，j 是组内编号。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。
输出最大价值。

数据范围
0 < N, V ≤ 100
0 < Si ≤ 100
0 < vij, wij ≤ 100

集合划分

\[f[i, j] = \max_{0 \leq k < si} (f[i-1, j], f[i-1, j-v[i, k]] + w[i, k]) \]

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 110;

int n, m;
int v[N][N], w[N][N], s[N];
int f[N];

int main()
{
    cin >> n >> m;

    for(int i = 1; i <= n; i++)
    {
        cin >> s[i];
        for(int j = 0; j < s[i]; j++)
            cin >> v[i][j] >> w[i][j];
    }

    for(int i = 1; i <= n; i++)
        for(int j = m; j >= 0; j--) //j循环至0的必要性在于每组中的每件物品的体积不同，无法直接在循环中限制v[i][k] <= j这一条件
            for(int k = 0; k < s[i]; k++)
                if(v[i][k] <= j)
                    f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);

    cout << f[m] << endl;
    return 0;
}