网络流(二)
最小割
最小割指的是,你需要在图上删掉尽可能少的边,代价为其边权,要使得两点 \(s,t\) 不连通。
一个著名的定理是:把边的边权看做容量,则最大流等于最小割。
平面图最小割
平面图的定义:
若图 \(G\) 能被画在平面上且不同的边仅在端点处相交,则称图 \(G\) 为平面图。
画出的没有边相交的图称为 \(G\) 的平面表示或平面嵌入。
平面图上 \(s,t\) 两点的最小割可以转化为其对偶图上两点间的最短路。
何为「对偶图」?把平面图的每个区域看做一个点,在平面图的每条边分割的两个区域对应的点间连边,得到的新图就是原平面图的「对偶图」。
我们以 P4001 ICPC-Beijing 2006 狼抓兔子 为例:考虑这样的一个割
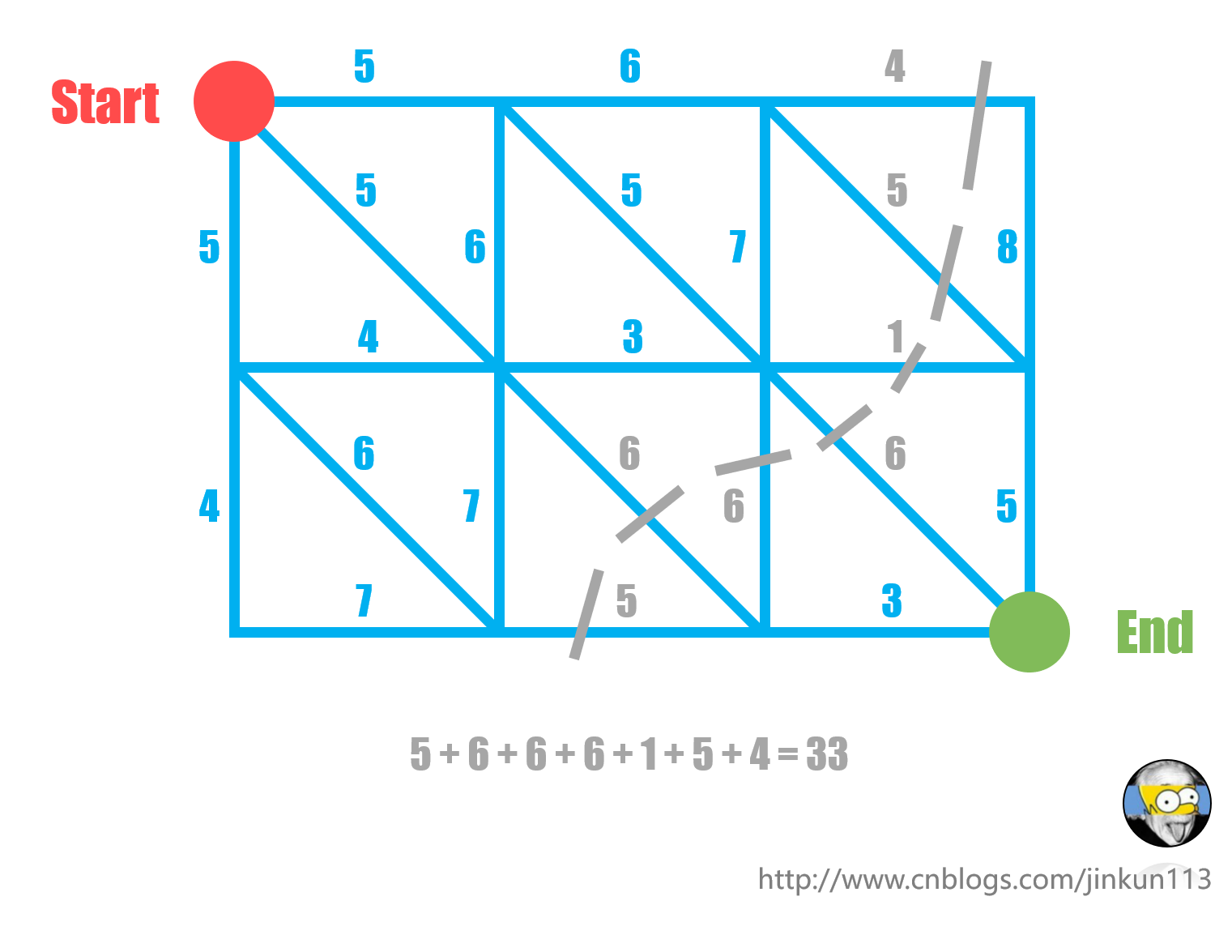
我们发现这恰好是从左下走向右上的一条路径,如图所示:
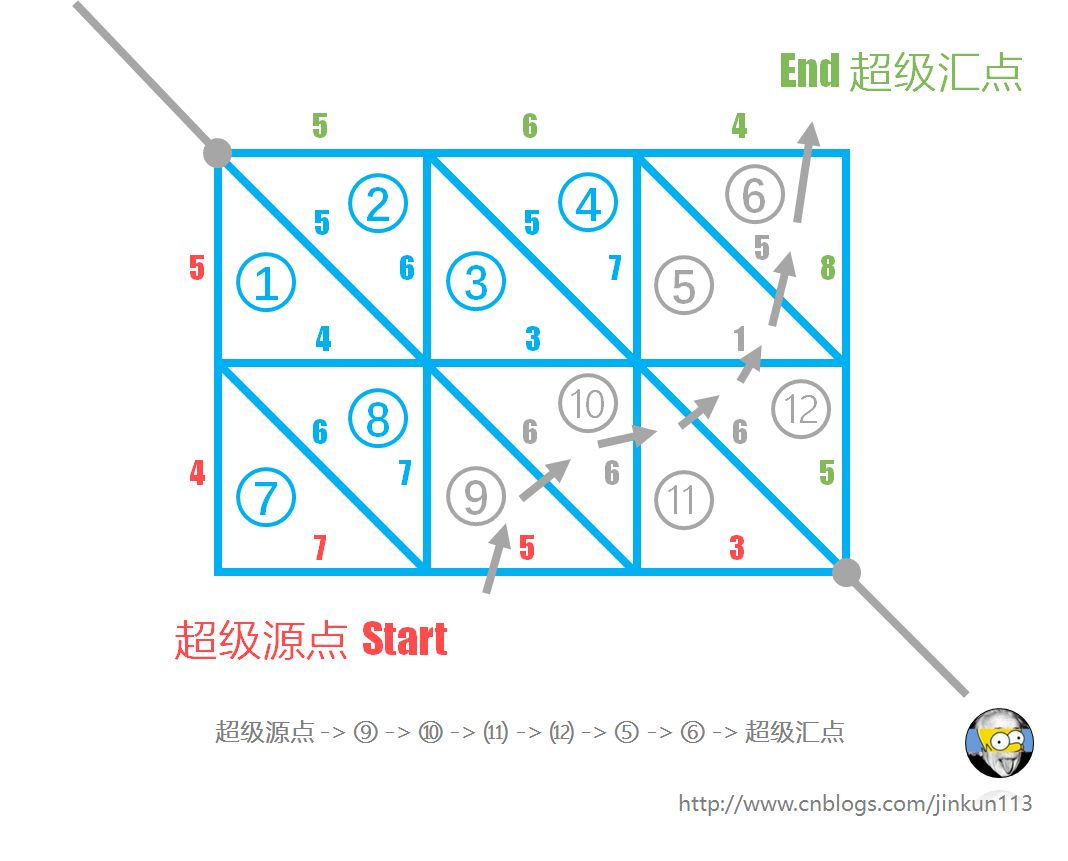
那么,我们要求的最小割也就变成了 \(s\to t\) 在对偶图中的一条最短路。
使用 \(\text{Dijkstra}\) 算法求解即可,复杂度 \(O(nm\log nm)\)。AC Code
最小割-例题
LuoguP2762 太空飞行计划问题
这个模型大概是这样的:
给定一张有向图,点有点权,点权可正可负。
对于一个子图,若其满足对子图内所有的点 \(u\), \(u\) 出边相连的所有点都在子图内,则称其为闭合子图。
你需要选出点权和最大的闭合子图。
可以发现,对于一个方案,其点权和就是:
- 「所有正权点的点权和」减去「未选出的正权点的点权和」再减去「选出的负权点的点权和(的绝对值)」。
那么我们只需要让后面两项的和尽可能小就行了。
建图:
- 从源点 \(s\) 向每个正权点连一条边,边权为其点权;
- 每个负权点向 \(t\) 连边,边权为其点权绝对值;
- 原图中所有的边仍然连上,边权为 \(\infty\)。
考虑一个闭合子图。可以发现一个重要的事情:如果我们砍掉所有选中的负权点与 \(t\) 之间的边,再砍掉所有未选中的正权点与 \(s\) 之间的边,那么 \(s,t\) 将会不连通。
因此,一个方案恰好对应了 \(s,t\) 之间的一个割。那么,跑一边网络流,求出最小割就可以了。
你也可以这么理解为何是最小割:考虑一个正权点,如果选了它,那么 \(s\) 到它的边就被连上了。要想让 \(s,t\) 不连通,中间的边权值都是 \(\infty\) 断不了,只能断掉其后继点与 \(t\) 之间的边。而这些边的边权和,正是选中该点所需要的代价。
当然上面的都是感性证明,不过我感觉已经足够能够理解「为何答案就是正权点权值和减去最小割」这件事了。
LuoguP2774 方格取数问题
很有代表性的一道题目。
像这种「从 \(n\) 个元素中选出若干,某些元素间互斥,不能同时选择,要求最大化价值和」的问题,有一个套路:
-
从源点 \(s\) 向每个连边,边权为该点价值;\(t\) 那边同理,不过边是反向的。
-
对于每一组互斥的点对,其必然分别位于两个集合中。连边,边权为 \(\infty\)。
-
求出最小割,所有点价值之和减去最小割就是答案。
为什么这样是对的?我们要让价值和最大化,就是最小化没有选择的那部分元素的价值。
对于任意一条路径 \(s\to u\to v\to t\),\((u,v)\) 间有连边代表 \(u,v\) 互斥。
由于最小割肯定不会去割那条边权为 \(\infty\) 的边,因此 \(s\to u\) 与 \(v\to t\) 两条边必然会被割掉一个。
这正符合了 「\(u,v\) 不能同时选择」的要求。或者你也可以把这个理解为二分图最大独立集。
当然上面是一个感性的证明。严格的证明可以轻易从这种思路推出来。
那么本题也就迎刃而解了。AC Code
LuoguP1361 小 M 的作物
类似上题,我们从 \(s\) 向每个点 \(i\) 连边,边权为 \(a_i\)。每个点 \(i\) 向 \(t\) 连边,边权为 \(b_i\)。
这样一来,要使 \(s,t\) 不连通,就必须割掉其中的一条边。这正好符合了「每个物品只能放在一个集合内」的约束。
此时还需要处理「同时选取某一组就会获得收益」的信息。
我们对于每一组新建一个点 \(s\),从 \(s\) 到 \(x\) 连边,边权为同时选这一组获得的收益。
转化一下就是,只要割掉了 \(s\) 到这一组内点的任意一条边,那么 \(s\to x\) 的边也必须断掉。
如何达到这个要求?只需要从 \(x\) 向组里的每个点都连一条边权为 \(\infty\) 的边即可。
这样一来,如果断掉了 \(s\) 到该组内一个点 \(u\) 的边,而 \(s\to x\) 的边没有被断掉,那么依然可以通过 \(s\to x\to u\) 到达 \(u\)。也就是说,\(s\to u\) 的边白断了......而最小割肯定不会干出这种事。
因此,如果断掉了 \(s\to u\) 的边,\(s\to x\to u\) 这条路径上肯定要断一条。
\(x\to u\) 边权为 \(\infty\),肯定不会断;因此,必然会断掉 \(s\to x\) 的边,也就是说得不到这个收益了。
这样本题就得到了解决。AC Code
可以发现,最小割可以用来解决这种「带有限制地选择,最大化价值」的问题。
使用上面的套路基本上已经可以轻松切掉大部分这类题目了。现在你随手就能切掉几十道紫题了!
随便选几个练一下:
二分图相关
二分图最大匹配
新建两个点 \(s,t\),从 \(s\) 连向每个左边的点,令其容量为 \(1\);每个右边的点连向 \(t\),容量为 \(1\)。
中间的边随便怎么设都行,\(\ge 1\) 就可以了。在这张图上跑网络流,可以发现最大流就等于最大匹配。
此外,在二分图上跑 \(\text{Dinic}\) 的复杂度是 \(O(m\sqrt{n})\) 。
二分图多重匹配
如果左边第 \(i\) 个点至多可以与右边 \(x_i\) 个点匹配,那么我们将 \(s\to i\) 这条边的容量设为 \(x_i\) 即可。右边同理。
注意此时中间的边的边权要设为 \(1\)。
二分图最小点覆盖
二分图最小点覆盖指的是,给定一张二分图,你需要找到一个尽可能小的点集 \(S\),使得图中任意一条边 \((u,v)\) 的两端点中至少有一个在 \(S\) 内。我们有如下定理:
二分图的最小点覆盖包含的点数等于其最大匹配的边数。
这个定理并不是很显然。我们来证明一下。
建图:从源点 \(s\) 向左侧每个点连边,边权为 \(1\);右侧每个点向 \(t\) 连边,边权为 \(1\);中间的边保留,边权为 \(\infty\)。
考虑这张图的一个割。中间的边肯定不会被砍掉。
如果 \(s\) 到左边一个点 \(u\) 的边被割掉了,或者右边一个点 \(u\) 到 \(t\) 的边被割掉了,那么那么我们在点集中选上 \(u\)。
我们现在证明这是一个合法的点覆盖:如果存在边 \((u,v)\),使得 \(u,v\) 都没有被选上,那么 \(s\to u,v\to t\) 两条边都没有被割掉。从而,\(s\to u\to v\to t\) 构成了 \(s\) 到 \(t\) 的一条合法路径,说明没有割开,矛盾了。
因此,我们证明了最小割等于最小点覆盖。
从而,「最小割」、「最大流」、「最大匹配」、「最小点覆盖」都相等。这就完成了证明。
进一步,若点有点权,要求点权和最小的点集覆盖,只需要将上面 \(s,t\) 连的边赋予边权跑最小割即可。
二分图的最大独立集
给定一张二分图,你需要选出尽可能多的点,满足这些点之间两两没有边。
这等价于删掉尽可能少的点与其相连的边,使得所有边都被删掉。
也就是说删掉的点要覆盖掉所有的边。要让这些点尽可能少,那就是求一个最小点覆盖。
因此,「二分图最大独立集的大小」就是「总点数」减去「二分图最小点覆盖的大小」。
有向无环图的最小路径覆盖
给定一张有向无环图,你需要找出最少的路径,使得这些路径经过了所有的点。
最小路径覆盖分为最小不相交路径覆盖和最小可相交路径覆盖,区别是这些路径是否可以相交。
不妨先来讨论不相交的情况。
我们这样考虑这个问题:一开始每个点都看做一条路径,此时的可能答案就是点的个数。
每次我们找一条边 \((u,v)\),如果 \(u\) 恰好是一条路径的结尾,\(v\) 恰好是一条路径的开头,那么可以将 \(u,v\) 所在的两条路径接在一起,答案就会减一。我们只需要尽可能多地进行路径的拼接即可。
将每个点 \(u\) 拆成两个点 \(u,u+n\)。左边放 \(n\) 个点代表路径的结尾,右边放 \(n\) 个点代表路径的开头。
对于图中的每条有向边 \((u,v)\),我们连边 \((u,v+n)\)。
此时的新图是一张二分图,考虑该二分图的一个匹配。如果选了 \((u,v+n)\) 这条边,就代表将上一条路径的结尾 \(u\) 与下一条路径的开头 \(v+n\) 拼到了一起。
每个点作为开头或结尾都只能被拼接一次,这恰好对应着匹配的定义。
要让拼接的次数尽可能大,只需要求出二分图的最大匹配就可以了。板子题 AC Code
题目选讲
LuoguP2763 试题库问题
感觉这个很简单啊。
- 从 \(s\) 向每个试题连边,容量为 \(1\);
- 每个试题向起所属类型连边,容量为 \(1\);
- 每个类型向汇点连边,容量需要这个类型的个数。
跑最大流就可以了。如果汇点那边没有全部满流就是 No Solution!。


 经典的图论算法。
经典的图论算法。

