网络流（一）

网络流（一）

网络流问题是这样的：

• 给定一个有向图 \(G=(V,E)\)，把图中的边看作管道，每条边有一个权值 \(c(u,v)\)，表示该管道的流量上限。
• 给定源点 \(s\) 和汇点 \(t\)，现在假设在 \(s\) 处有一个水源，\(t\) 处有一个蓄水池，问从 \(s\) 到 \(t\) 的最大水流量是多少，类似于这类的问题都可归结为网络流问题。
• 从 \(s\) 到 \(t\) 的一条可流路径称之为增广路。

让我们来对它进行一个形式化。考虑流 \(f\)，它需要满足的条件有：

• 流量不能超过容量。\(f(u,v)\le c(u,v)\)。
• 对于每个点，流进了多少水，就要流出多少水。\(\forall u,\sum_{x}f(x,u)=\sum_{x}f(u,x)\)。
• 为了方便起见，我们还定义一条边的反向边 \((v,u)\) 的流量满足 \(f(v,u)=-f(u,v)\)。稍后我们将会看到这么做有什么用。

对于一个流 \(f\)，残量网络定义为一个点集与边集都和原图相同的图，但 \((u,v)\) 的边权为 \(c(u,v)-f(u,v)\)。

Start

一个显然的想法是考虑贪心：对于一条增广路，我们找到路上的边权最小值 \(x\)，然后将路径上每条边都减去 \(x\)；不断找增广路，最后没有增广路的时候就认为算法结束。

然而有一个很显然的反例：

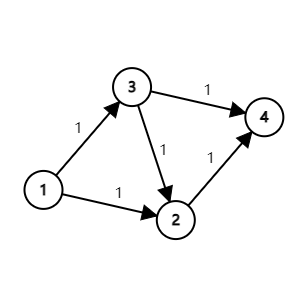
如果我们不幸地选了 \(1\to 3\to 2\to 4\) 这条增广路，那么一下子就不存在增广路了，求出的流大小为 \(1\)；

然而更优的是 \(1\to 3\to 4\) 与 \(1\to 2\to 4\) 这两条路径，这样的流大小为 \(2\)。

解决方法是建立反向边。我们如果在一条边 \((u,v)\) 上添加了一个大小为 \(k\) 的流，那么不仅要将边 \((u,v)\) 的边权减去 \(k\)，同时还将其反向边 \((v,u)\) 的边权加上 \(k\)。这可以看做一种「反悔」机制。

实际上回忆上面「流」的第三条性质，我们将 \(f(u,v)\) 加上 \(k\) 的同时，自然要给 \(f(v,u)\) 减去 \(k\)。由于残量网络上的边权是 \(c(v,u)-f(v,u)\)，这条边的边权就会加上 \(k\)。

那么我们就有了大致的算法框架：每次在图上只沿着容量 \(>0\) 的边走，如果找到 \(s\) 到 \(t\) 的一条路径，设路径上边权的最小值为 \(w\)，那么就将这条路径上所有边的边权都减去 \(w\)，同时将每条边反向边的边权 \(+w\)，并将最大流的值加上 \(w\)；如果 \(s\) 与 \(t\) 不连通，就认为无法增广，算法结束。

如果每次任意找一条增广路进行增广，我们就得到了 \(\text{Ford-Fulkerson}\) 算法。

你想必有这样的疑惑：建完反向边后，一条边可能会被访问很多次，算法的效率将会很低下；甚至于，增广会不会一直进行下去？我们敏锐地注意到每次增广后最大流必然严格增长，因此增广不会无限地进行下去。但，这仍然无法改变算法效率低下的事实。

事实上，这个算法确实很容易被卡掉。如图所示：（借算导上的图）

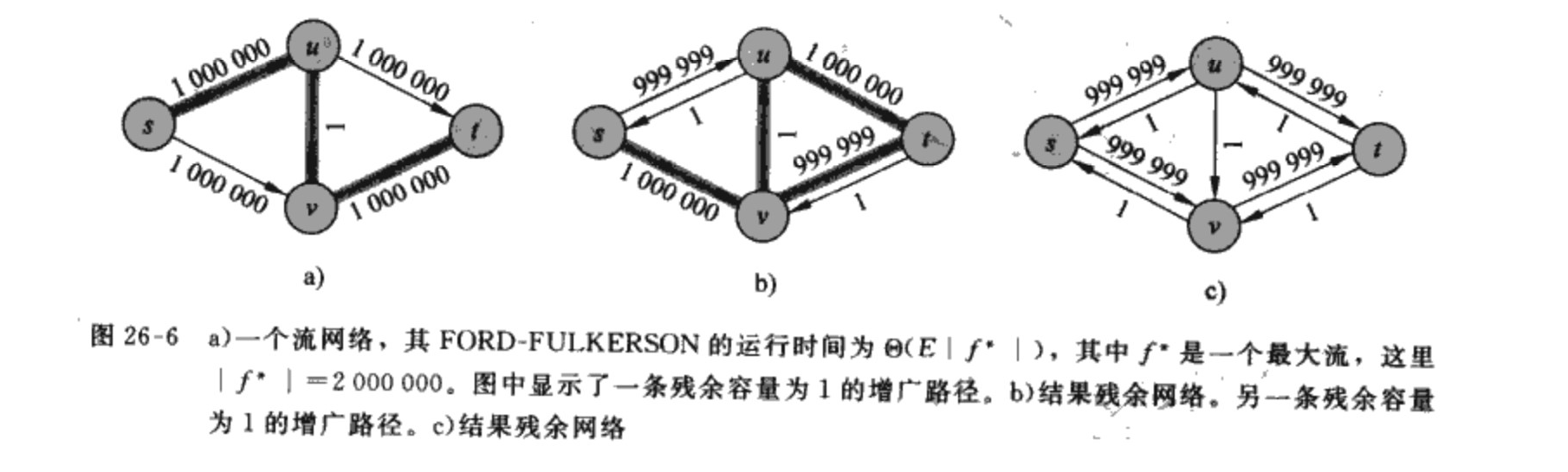
Edmond-Karp 增广路算法

我们来进行一些优化。

你想必早已听说过：只要每次使用 \(\text{BFS}\) 找到 \(s\to t\) 的一条最短增广路，增广次数将不超过 \(O(nm)\)。

这里我们来简要证明一下它的复杂度。

对于一条增广路 \(p\)，如果其上一条路径 \((u,v)\in p\) 满足其容量 \(c(u,v)\) 恰为 \(p\) 中所有路径的容量最小值，则称其为 \(p\) 上的关键边。一条增广路上可以有多条关键边。

显然，每条增广路上都至少有一条关键边。这意味着增广路的个数不会超过关键边的个数，也就是说，增广次数不会超过关键边的总数。

我们将证明：每条边成为关键边的次数不超过 \(O(n)\)。一旦该结论成立，关键边的总数将为 \(O(nm)\)，则增广次数不超过 \(O(nm)\)。

为了证明这一结论，我们记 \(\text{Dist}(u)\) 为 \(s\to u\) 的最短路长度，这里边的权重为 \(1\)，且只能经过边权 \(>0\) 的边。

可以证明，无论如何增广，\(\text{Dist}(u)\) 必然不会减少。

对于一条边 \((u,v)\)，当其成为关键边时，由于我们走的是最短路径，故必有 \(\text{Dist}(v)=\text{Dist}(u)+1\)。

由于这条边是增广路上的关键边，因此在增广过后这条边的残存容量将降至 \(0\)；反向边的容量则会相应增加。

想要让这条边再次成为关键边，必须要存在一次增广，使得增广路经过其反向边 \((v,u)\)。

记增广后的最短路长为 \(\text{Dist'}\)，那么有 \(\text{Dist'}(u)=\text{Dist'}(v)+1\le \text{Dist}(v)+1=\text{Dist}(u)+2\)。

这表明每条边每成为一次关键边，\(s\) 到其一端点的最短路长就会 \(+2\)。最短路长最多为 \(n-2\)，则每条边成为关键边的次数不超过 \(\dfrac{n-2}{2}=O(n)\)。这样就完成了我们的证明。

上面的证明其实主要在说明一个事：每条边被访问的次数并不会太多。

由于 \(\text{BFS}\) 的复杂度是 \(O(n+m)\)，该算法的总时间复杂度为 \(O(nm(n+m))=O(nm^2)\)。

Dinic 算法

在 \(\text{Dinic}\) 算法中，我们每次增广前先将图分层。节点 \(u\) 的层次 \(d_u\) 被定义为 \(s\to u\) 最少需要经过的边数。

一次 \(\text{BFS}\) 即可完成分层。分层后，若无法求出 \(t\) 的层次，则不存在增广路，算法终止。

在增广的时候，我们只走满足 \(d_v=d_u+1\) 的边 \((u,v)\)。我们称满足上面等式的边为允许弧。

增广的操作使用 \(\text{DFS}\) 来实现。与 \(\text{Edmond-Karp}\) 算法不同的是，\(\text{Dinic}\) 算法每次会增广多条路径。

\(\text{DFS}\) 的过程中，我们从 \(s\) 出发，每次只走允许弧，同时记录一下流到当前节点时最多能流入的流量 flow；在访问一个节点 \(u\) 时，我们遍历其在残量网络上的每条出边 \((u,v)\)，对 \(v\) 进行 \(\text{DFS}\)（此时传入的 flow 即为 \(\min\{\texttt{flow}-\sum k_v,c(u,v)\}\)），并返回从 \(v\) 所能流出的最大流量 \(k_v\)。\(\text{DFS}\) 的返回值就是 \(\sum_v{k_v}\)。

可以证明，\(\text{Dinic}\) 算法的时间复杂度为 \(O(n^2m)\)，实际表现则快得多，甚至可以处理 \(n,m\le 10^5\) 的网络。

值得一提的是，\(\text{Dinic}\) 算法求解二分图最大匹配的复杂度是 \(O(m\sqrt{n})\)；更一般地，而在边权均为 \(1\) 的图上跑 \(\text{Dinic}\)，复杂度将会是 \(O(m\cdot\min(\sqrt{m},n^{0.67}))\)。

\(\text{Dinic}\) 算法有一个效果显著的优化——当前弧优化。

我们注意到，在一次增广中，如果一条边的流量已经满了，那么这次增广无论如何都不会再走这条边了。

因此，我们对每个节点 \(u\) 记录一条「当前弧」，表示 \(u\) 下一条应该增广的边。下次访问 \(u\) 时，直接从当前弧开始往后遍历出边，就省下了遍历前面那些已经满流的边的时间。

代码实现

int head[MN],nxt[MN],edge[MN],ver[MN],tot=1;
int now[MN],d[MN],n,m,s,t;

void adde(int x,int y,int z){
	ver[++tot]=y,edge[tot]=z,nxt[tot]=head[x],head[x]=tot;
	ver[++tot]=x,edge[tot]=0,nxt[tot]=head[y],head[y]=tot;
}

queue<int>q;

bool bfs(){
	memset(d,0,sizeof(d));
	while(q.size())q.pop();
	q.push(s),d[s]=1,now[s]=head[s];
	while(q.size()){
		int u=q.front();q.pop();
		for(int i=head[u];i;i=nxt[i]){
			if((!edge[i])||d[ver[i]])continue;
			int v=ver[i];now[v]=head[v];
			d[v]=d[u]+1,q.push(v);
			if(v==t)return 1;
		}
	}
	return 0;
}

int dinic(int u,int flow){
	if(u==t)return flow;
	int rest=flow;
	for(int i=now[u];i&&rest;i=nxt[i]){
		now[u]=i;int v=ver[i];
		if(d[v]==d[u]+1&&edge[i]){
			int k=dinic(v,min(rest,edge[i]));
			if(!k)d[v]=0;//去掉增广完毕的节点
			edge[i]-=k,edge[i^1]+=k,rest-=k;
		}
	}
	return flow-rest;
}

void solve(){
	n=read(),m=read(),s=read(),t=read();
	for(int i=1;i<=m;i++){
		int u=read(),v=read(),w=read();
		adde(u,v,w);
	}
	int flow=0,ans=0;
	while(bfs()){
		while(flow=dinic(s,INF))ans+=flow;
		//让一次 BFS 得出的结果可以使用多次
	}
	cout<<ans<<endl;
}