置换群、等价类计数与 Burnside 引理

群、置换与置换群

本文中 群 部分的内容只用于证明 $\text{Burnside}$ 引理中的一个小结论，所以介绍的有可能不够周全。

群

大家都知道，一个集合 $G$ 与 $G$ 上的二元运算 $\cdot$ 如果满足：

• 结合律：$a\cdot (b\cdot c)=(a\cdot b)\cdot c$
• 有单位元：存在 $e\in G$ 满足对任意的 $ae=ea=a$。（这里 $ab$ 指 $a\cdot b$）
• 逆元存在：对任意的 $a\in G$ 均存在 $a^{-1}\in G$ 使得 $aa^{-1}=e$

那么我们就称 $(G,e,\cdot)$ 构成一个群。有时也记作 $(G,\cdot)$。

此外，若 $(G,\cdot)$ 只满足结合律，我们称其为半群；若 $(G,\cdot)$ 不仅满足结合律还存在单位元，就称其为幺半群。

例如，$(\mathbb Q,0,+)$ 是一个群，$\{0,1,2,\cdots,m-1\}$ 关于 $\bmod m$ 意义下的加法构成群，其单位元为 $0$；而 $(\mathbb R,1,\times)$ 不是群，因为 $0$ 不存在逆元。

子群

对于群 $(G,\cdot)$，若 $G$ 的非空子集 $H\subseteq G$ 满足 $H$ 对 $\cdot$ 这一运算仍然构成群，我们就称 $H$ 是 $G$ 的子群，记作 $H\le G$。

例如，考虑 $G=\mathbb Z,H=\{3x|x\in\mathbb Z\}$，运算 $\cdot$ 为整数加法 $a\cdot b=a+b$，那么 $(G,\cdot)$ 构成群，$(H,\cdot)$ 同样构成群，因此 $H\le G$。

陪集

对于群 $(G,\cdot)$ 与其子群 $H\le G$，考虑一个元素 $a\in G$，我们称

$$aH=\{ah|h\in H\}$$

与

$$Ha=\{ha|h\in H\}$$

为 $H$ 的陪集。$aH$ 称为 $H$ 的左陪集，$Ha$ 则是 $H$ 的右陪集。

直观来看，陪集可以看做将集合 $H$ 在 $G$ 上进行了「平移」，从而得到了另外一个集合。例如，对于群 $H=\{3x|x\in \mathbb Z\}$ 与整数加法构成的群，它的一个陪集就是 $2H=\{3x+2|x\in \mathbb Z\}$。

对于有限群 $G$ 以及其子群 $H\le G$，我们有以下结论：

• $|aH|=|H|$。这是因为对于 $b,c\in H$，$b\neq c$，那么必然有 $ab\neq ac$，否则有 $a^{-1}ab=a^{-1}ac\Rightarrow b=c$ 矛盾。
• 若 $a\in H$，则 $aH=H$。这是因为 $H$ 关于运算 $\cdot$ 构成群，故此时 $\forall h\in H$ 我们有 $ah\in H$，又由 $|aH|=|H|$ 可知 $aH=H$。
• 对任意的 $a,b\in G$，要么 $aH=bH$，要么 $aH\cap bH=\varnothing$。证明与上一条类似。

注意上述结论在无限群上不一定成立，例如 $G=(\mathbb{Z}\setminus\{0\},\times,1)$，考虑集合 $H=\{2x|x\neq 0,x\in \mathbb Z\}$ 与整数乘法构成的子群，设 $a=2\in H$，则 $aH=\{4x|x\neq 0,x\in \mathbb Z\}\neq H$。

Lagrange 定理

对于群 $G$ 以及其子群 $H$，考虑 $G$ 中 $H$ 的本质不同的陪集个数，这个数称为 $H$ 在 $G$ 中的指数，记作 $[G:H]$。

$\text{Lagrange}$ 定理指出，$H$ 在 $G$ 中的指数恰为 $G$ 的大小与 $H$ 的大小的商，即 $[G:H]=\frac{|G|}{|H|}$。

我们可以感性地理解这一点：子群 $H$ 的陪集可以看作 $H$ 在 $G$ 上的平移，而各个陪集之间两两不交，因此 $H$ 的所有陪集构成了 $G$ 的一个分割。（实际上我们还需要说明，对于任意的 $a\in G$，考虑取 $h\in H$ 以及 $x=h^{-1}a$，那么 $xH$ 这一陪集就是包含 $a$ 的一个陪集。）而所有陪集大小相等，因此 $|H|\times [G:H]=|G|$ 成立。

置换

设有限集合 $U=\{a_1,a_2,\cdots,a_n\}$，我们称 $U$ 的一个置换 $A$ 为一个双射 $f:U\to U$，记作

$$A=\begin{pmatrix}a_1&a_2&a_3&\cdots&n\\a_{p_1}&a_{p_2}&a_{p_3}&\cdots&a_{p_n}\end{pmatrix}$$

其中 $p_i=f(i)$，是一个排列。不难发现置换其实就是一个排列。

置换群

由置换构成的群叫做置换群。

其中，这个群的单位元为 $f(x)=x$ 这一单位置换，二元运算为 $f\circ g(x)=g(f(x))$。

由 $n!$ 个 $n$ 元置换构成的群记作 $S_n$。置换的乘法不具有交换律。

轮换

若一个置换可以表示为

$$A=\begin{pmatrix}a_1&a_2&\cdots&a_{n-1}&a_n\\a_2&a_3&\cdots&a_n&a_1\end{pmatrix}$$

我们就称 $A$ 是一个轮换。任意置换都能被分解成若干轮换的乘积。

直观来看，如果我们把一个置换看做一张 $n$ 点 $n$ 边的有向图，图中的每个点 $i$ 都有且仅有一条出边 $i\to p_i$，那么考虑该图中的一个连痛块，这个联通块必然是一个大环。换言之，这张图实际上就是若干个环，那么各个环相互独立，一个置换自然就能分解成若干轮换。有时，我们也把这样的一个环叫做置换环。

对于上面的轮换 $A$，可以简记为 $A=(a_1,a_2,\cdots,a_n)$。

我们可以用轮换的乘积来表示一个置换 $A$，例如，对于 $p=(4,3,2,1)$，写成轮换的形式就是 $(2\quad 3)(1\quad 4)$ 。

例题1.1

给出一个置换 $A$，请你求出最小的正整数 $k$，满足 $A^k$ 是单位置换。

单位置换指的是，，$I=\begin{pmatrix}a_1&a_2&\cdots&a_n\\a_1&a_2&\cdots&a_n\end{pmatrix}$，也就是将原序列保持不变。

例如，对于 $A=\begin{pmatrix}1&2&3&4\\3&4&1&2\end{pmatrix}$，我们有 $A\times A=\begin{pmatrix}1&2&3&4\\1&2&3&4\end{pmatrix}$，因此 $k=2$。

解答

我们把 $A$ 拆成若干轮换，设它们的大小分别为 $x_1,_2,\cdots,x_m$，那么答案就是 $\text{lcm}(x_1,x_2,\cdots,x_m)$。证明留给读者。

其中，$\text{lcm}(a,b)$ 指的是 $a,b$ 的最小公倍数，即最小的 $w$ 满足 $a\mid w,b\mid w$。多个数的 $\text{lcm}$ 的定义是类似的。

例题 1.2

给出一个排列 $p$，每次你可以交换排列中的两个数（不一定相邻），那么至少交换多少次能使对每个 $i=1,2,\cdots,n$，都有 $p_i=i$？

解答

我们把 $p$ 拆成若干置换环，如果拆成了 $k$ 个置换环，那么答案就是 $n-k$。

这是因为：

• 对于单位置换，其置换环的个数为 $n$（即 $n$ 个大小为 $1$ 的自环）。
• 对于一个排列，交换两个数之后，其置换环的个数最多改变 $1$。

第一条性质是显然成立的。对于第二条，考虑下面这个图

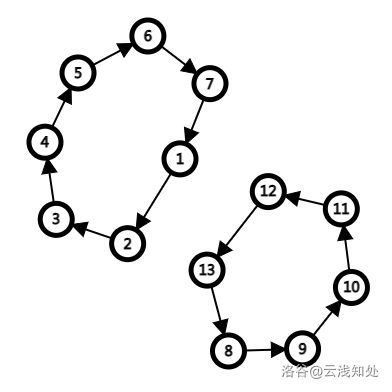
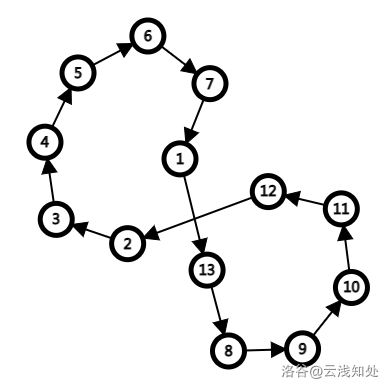
左图中的 $p=(2,3,4,5,6,7,1,9,10,11,12,13,8)$，左图到右图的操作为 $\text{swap}(p_1,p_{12})$。

可以发现，如果我们 $\text{swap}$ 的两个点在不同置换环内，那么置换环个数会减一（即左图 -> 右图）；否则，置换环个数会加一（即右图 -> 左图）。这样就完成了证明。

等价类计数

$\text{Burnside}$ 引理可以用于对部分「等价类计数」问题进行转化。

等价类计数

这类问题一般会给出一个集合 $S$ 以及 $S$ 上的置换群 $G$，对于 $a,b\in S$，若存在置换 $f\in G$ 使得 $f(a)=b$，我们就认为 $a,b$ 等价。

等价关系具有传递性，我们把等价关系看成一条无向边，那么这类问题一般需要我们求出来图中的联通块个数，也就是等价类的个数。

染色问题

考虑这样一个问题：

• 你要给一个 $2\times 2$ 的方格染色，每个格子可以染成黑白两种颜色。
• 显然，一共有 $2^4=16$ 种不同的染色方案。
• 现在我们加一个条件：如果两个染色方案可以经过若干次顺时针旋转 $90^{\circ}$ 变成相同的，那么我们就认为这两种方案是一样的。
• 问此时还有多少种不同的染色方案。

例如，下面四种染色方案都是相同的。

10 01 00 00
00 00 01 10

Burnside 引理

在本题中，所有元素的集合 $S$ 就是这 $2^4=16$ 种染色方案，置换群为 $G=\{0^{\circ},90^{\circ},180^{\circ},270^{\circ}\}$。其中 $x^{\circ}$ 指的是 将图形顺时针旋转 $x^{\circ}$。

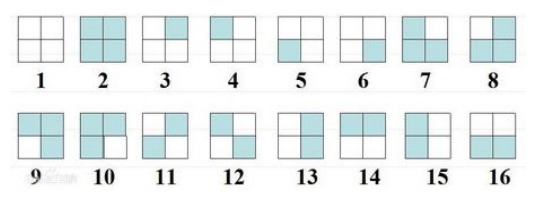
我们列出这 $16$ 种状态：

我们约定：

• $Z_x$ 表示 $G$ 中施加在 $x$ 上之后所得结果仍然为 $x$ 的置换集合，即 不动点 的集合。

例如，$Z_1=Z_2=\{0^{\circ},90^{\circ},180^{\circ},270^{\circ}\},Z_3=\{0^{\circ}\},Z_{11}=Z_{12}=\{0^{\circ},180^{\circ}\}$。

• $E_x$ 表示 $x$ 在施加 $G$ 中任意置换之后，所能到达的状态集合，又称作 $x$ 的 轨道。

例如，$E_1=\{1\},E_3=\{3,4,5,6\},E_{12}=\{11,12\}$。

• $D(g)$ 表示在置换 $g$ 下保持不变的状态个数。

例如，$D(90^{\circ})=\{1,2\},D(180^{\circ})=\{1,2,11,12\}$。

那么，我们有以下结论：

$$\forall x\in S,|{E}_x|\times |{Z}_x|=|G|$$

你可以用上面的例子验证一下这个结论。

我们发现，如果把 ${Z}_x$ 与置换乘法构成的群看做 $G$ 的一个子群，那么 $|{E}_x|$ 实际上就是 $Z_x$ 的陪集个数。由 $\text{Lagrange}$ 定理可知，该结论确实是成立的。

接下来，我们设 $L$ 是本质不同的等价类个数，我们发现

$$\sum_{g\in G}D(g)=\sum_{x\in S}|E_x|=\sum_{i=1}^L|G|=L\times |G|$$

前两个等号的原理都是简单的交换求和顺序。第二个等号用到了 $|G|=|E_x||Z_x|$ 这一结论。

移项之后，我们就得到了 $\text{Burnside}$ 引理：

$$L=\dfrac{1}{|G|}\sum_{g\in G}D(g)$$

直观来看，$\text{Burnside}$ 引理指的是，考虑置换群中的每一种置换 $g$，我们计算出在这个置换下保持不变的状态个数 $D(g)$（通常这一步需要用到组合计数相关的技巧），全部加起来再除以 $|G|$ 就是答案。

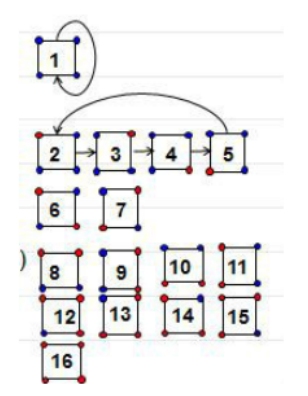
我们回到「染色问题」上，此时 $G=\{0^{\circ},90^{\circ},180^{\circ},270^{\circ}\}$，保持不变的状态个数分别为 $16,2,4,2$，因此答案为 $\frac{16+2+4+2}{4}=6$。如下图，可以看到确实如此。

染色问题-Ex

仍然是 $2\times 2$ 的正方形，但是可以染的颜色有 $m$ 种，怎么做？

我们考虑给方格编个号，如图所示：

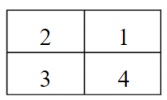
我们把 $G$ 中的元素写成置换：

• 转 $0^{\circ}$：写成轮换的形式就是 $(1)(2)(3)(4)$。
• 转 $90^{\circ}$：即 $1\to 4,4\to 3,3\to 2,2\to 1$，那么就是 $(4\quad3\quad2\quad1)$。
• 转 $180^{\circ}$：即 $(1\quad 3)(2\quad 4)$。
• 转 $270^{\circ}$：$1\to 2,2\to 3,3\to 4,4\to 1$，因此是 $(1\quad2\quad3\quad4)$。

考虑一个轮换，不难发现，轮换中涉及到的元素必须都相等。

例如，想要让这个图形转 $180^{\circ}$ 后保持不变，那么 $1,3$ 的颜色必须相同，$2,4$ 的颜色必须相同。

那么对于置换 $g$，设 $c(g)$ 为 $g$ 所能拆成轮换的个数，可以发现，$D(g)=m^{c(g)}$。

因此我们得到

$$L=\frac{1}{|G|}\sum_{g\in G}m^{c(g)}$$

这其实就是 $\text{Polya}$ 定理。其实只需要记住 $\text{Burnside}$ 引理就够了。

题目选讲

这里选取了一些经典的例题。

Luogu4980【模板】Pólya 定理 Present 7.0

求用 $m$ 种颜色染一个点数为 $n$ 的手链有多少种本质不同的方案数。

能够在旋转后重合的两种方案被视作相同的方案。

$1\le n,m\le 10^9$，答案对 $10^9+7$ 取模。本题中 $n=m$。

本题中置换有 $n$ 种，分别是转 $0,1,\cdots,n-1$ 格。不难发现这 $n$ 种置换构成置换群。

考虑转 $x$ 格的置换，其对应的排列是 $p_i=(i+x)\bmod n$。

可以发现这会构成 $\gcd(n,x)$ 个置换环，因此不动点的个数为 $m^{\gcd(n,x)}$。那么我们要算的就是

$$\sum_{x=0}^{n-1}m^{\gcd(n,x)}$$

注意到 $\gcd(n,x)$ 必然是 $n$ 的约数，考虑套路地交换求和顺序，有

$$\sum_{x=0}^{n-1}m^{\gcd(n,x)}=\sum_{d|n}\varphi(n/d)m^d$$

现在我们要计算 $n$ 的所有约束的 $\varphi$ 值，考虑直接找出来 $n$ 的唯一分解，然后 $\text{DFS}$ 枚举各质因子的指数即可。

这样做的时间复杂度为 $O(\sqrt{n}\log n)$，$\log$ 来自快速幂。AC Code

Luogu1446 HNOI2008 Cards Present 7.5

题目中给出的 $m$ 种「洗牌法」其实构成了一个置换群。

考虑 $\text{Burnside}$ 引理，对于一个置换，我们将其拆成若干轮换，要使牌堆构成不动点，每个轮换中的牌的颜色必须都相等。

设拆成了 $k$ 个轮换，大小分别为 $x_1,x_2,\cdots,x_k$，我们考虑 DP：设 $f(i,a,b,c)$ 表示前 $i$ 个置换环，分别用 $a,b,c$ 张红、蓝、绿牌的方案数，转移枚举最后一个置换环所用颜色即可。

记 $k=\max\{S_r,S_g,S_b\}\le 20$，那么这样做的时间复杂度为 $O(m^2k^3)$，已经能够通过本题。

注意到 DP 的过程中 $a+b+c$ 实际上是一个定值，因此可以优化到 $O(m^2k^2)$。

我偷懒写了 $O(m^2k^3)$ 的 AC Code

Luogu2561 AHOI2002 黑白瓷砖 Present 7.0

显然置换群可以用「保持不变」，「顺/逆时针转 $120^{\circ}$」，「关于某条对称轴翻转」一共六种置换来表示。

对于「保持不变」，显然置换环个数为 $\frac{n(n+1)}{2}$。

对于「顺/逆时针转 $120^{\circ}$」，画个图手玩一下可以发现，设 $f(n)$ 表示 $n$ 层的置换环个数，那么最外面一层会形成 $n-1$ 个置换环，然后转化为 $n-3$ 层的情况，因此 $f(n)=f(n-3)+n-1$。

对于「关于某条对称轴翻转」，考虑第 $2k$ 行会有 $k$ 个环，$2k+1$ 行会有 $k+1$ 个环，可以得到置换环个数为 $\frac{1}{2}\left(\frac{n(n+1)}{2}+\lceil\frac{n}{2}\rceil\right)$。

注意，计算的时候，为了让我们的置换构成置换群，必须要把「关于某条对称轴翻转」这一操作算三遍，即关于三条对称轴翻转（尽管在这三个置换下不动点的个数都是相同的），才能保证这些置换构成一个群。因此置换群的大小实际上是 $6$ 而非 $4$

代码就不放了吧？唯一的难度在于高精度 23333

Luogu4128 SHOI2006 有色图 Future 8.4

什么，哪里有涩图，我有个朋友想要

本题中置换群为全体长为 $n$ 排列构成的集合 $S_n$。

考虑一个排列 $p$，如果将其对应的置换施加在这个图上会使图保持不变，那么对任意的 $i\neq j$，必然有边 $(i,j)$ 与边 $(p_i,p_j)$ 同色。

我们令 $i,j$ 同属一个置换环，那么可以得到：对于一个置换环，设其中的点依次为 $x_1\to x_2\to \cdots\to x_k(\to x_1)$，那么对于一个固定的 $d$，任意距离为 $d$ 的点对之间的连边的颜色都必须相等。

也就是说，若一个置换环的大小为 $k$，那么这个置换环内部边的颜色共有 $m^{\lfloor k/2\rfloor}$ 种方案。

接下来考虑跨越置换环的边：对于两个大小分别为 $a,b$ 的置换环，会形成 $a\times b$ 条边。

手玩一下可以发现，这些边的方案数实际上是 $m^{\gcd(a,b)}$。

例如，$a=3,b=5$ 时，我们可以推出 $(1,1)=(2,2)=(3,3)=(1,4)=(2,5)=(3,1)=(1,2)$。一直推下去就可以得到这 $3\times 5=15$ 条边必须全都一样。你可以试着手玩一下 $a=2,b=4$ 的情况。

那么现在的问题转化为：

对于排列 $p$，设其置换环的大小分别为 $x_1,x_2,\cdots,x_k$，有

$$w(p)=\prod_{i=1}^km^{\lfloor x_i/2\rfloor}\times \prod_{i\neq j}m^{\gcd(x_i,x_j)}$$

那么答案就是 $\dfrac{1}{n!}\sum_{p}w(p)$。

显然直接枚举排列算是不行的。

我们可以发现，如果两个排列的置换环大小全都相同，那么它们的贡献也是一样的。

因此考虑枚举 $n$ 的拆分并计算贡献。具体来说我们枚举 $x_1\ge x_2\ge x_3\ge\cdots\ge x_k$ 且 $\sum x_i=n$ 的所有序列 $x$，然后计算有 $k$ 个置换环，且大小分别为 $x_1,x_2,\cdots,x_k$ 的排列的个数。

这个怎么算呢，我们考虑一个大小为 $a$ 的置换环，其内部的方案数为 $(a-1)!$（就是圆排列），然后外面要把 $n$ 分配给这些置换环，因此有一个多重组合数 $\binom{n}{x_1,x_2,\cdots,x_k}=\frac{n!}{\prod x_i!}$ 的贡献。然后我们考虑所有大小为 $r$ 的置换环，可以发现这些置换环之间相互交换顺序其实是没区别的。因此系数就是

$$\dfrac{n!}{\prod x_i\prod_rc_r!}$$

其中 $c_r$ 表示大小为 $r$ 的置换环个数。

由于 $n\le 53$，拆分数实际上并不多，我们暴力枚举的时间并不会太大。

AC Code，挺好写的

练习题

• POJ2409 Let it Bead <- 这题的题意挺迷的，我搜了搜题解才发现操作有翻转和旋转两种orz|参考代码
• Luogu4727 图的同构计数 <- 双 倍 经 验
• Luogu3307 SDOI2013 项链 <- 其实没啥思维难度，评黑估计完全是因为麻烦。。|参考题解