AtCoder Beginner Contest 257(C~G)
AB 不写了
UPD: 更新了 G 的题解
ABC257C Robot Takahashi
按照 排个序,算一下前缀后缀 1 和 0 的个数就行了。答案大概是一个 的形式。
有一个小细节:排序之后 时无法在 之间断开,要特判。我因为这个 WA 了一发。
ABC257D Jumping Takahashi 2
二分答案,然后暴力建图 dfs 就行了。。注意二分的右端点不能太小也不能太大。我思考了一下感觉至少要开到 ,然后无脑开了 结果一下子爆 long long 了,又 wa 了一发2333
ABC257E Addition and Multiplication 2
我们发现如果确定了每个数 要买几个,那么最优方案肯定是从 到 一个一个放下来。
因此考虑用一个长度为 的 vector 来表示每一个数字选了多少个,然后随便 dp 一下就行了。
时间复杂度 。感觉看代码更好理解:AC Code
ABC257F Teleporter Setting
考虑新建一个假的点 ,对每个 的边连边 。
现在相当于对每个 要算出来如果加上边 之后 的最短路。
这个是经典问题,直接正反跑两遍单源最短路算出来 表示 的最短路,那么答案就是 中的最小值。本题中边权都是 ,直接 BFS 即可。复杂度 。
ABC257G Prefix Concatenation
考虑 dp:设 为前缀 的答案,那么转移方程大概是 的一个形式。但是满足这个条件的 并不是一段区间,不好优化。
正着 dp 不好做,我们考虑倒过来:设 为后缀 的答案,则 。
那么设 为 与 的 LCP 长度, 就要满足 ,这样就变成单点修改区间求 min 了。线段树直接做,。
AC Code,跑的飞快,最慢 197ms。
后记
《五彩斑斓的世界》
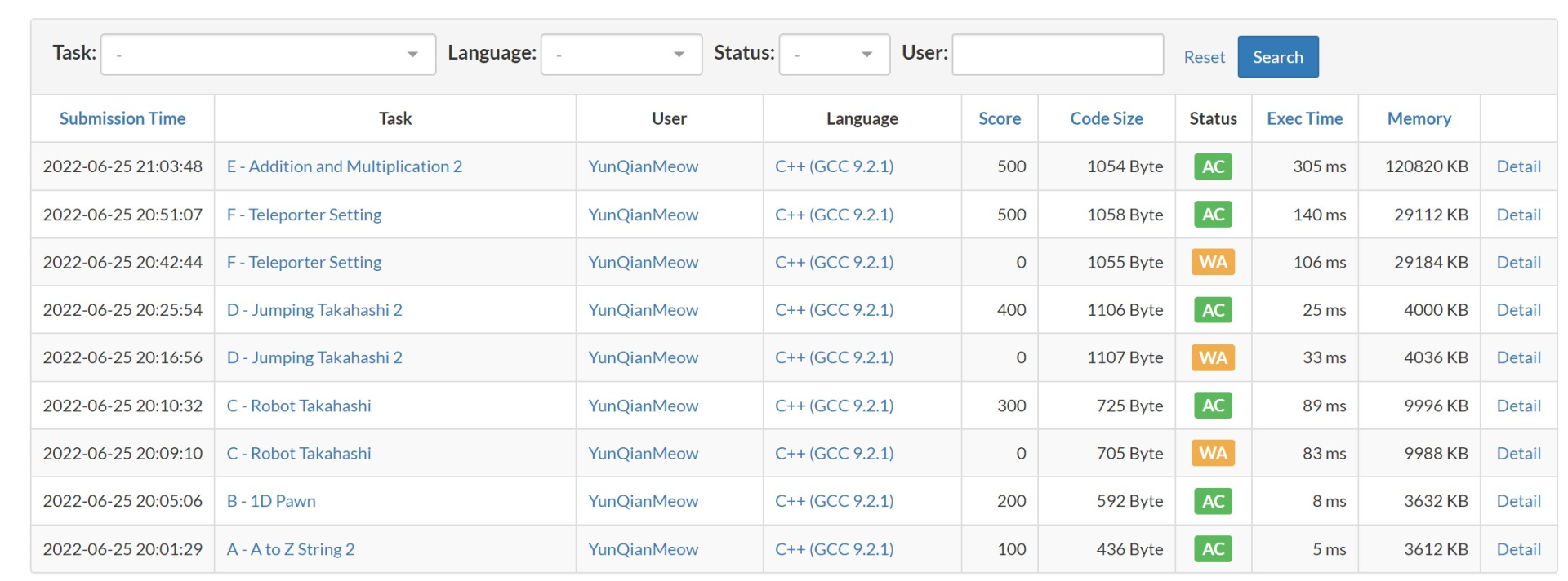


 萌新的 AT 下分记录
萌新的 AT 下分记录


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】