2022.8.12 做题记录

Luogu6453 PERIODNI Future 7.5

考虑直接 DP，发现貌似不太行......我想到的只有设 \(f(i,j,k,l)\) 表示前 \(i\) 列，最后一列必须放且放在第 \(j\) 行，上一个在第 \(k\) 列的第 \(l\) 行的方案数。光是状态数已经达到了 \(O(n^2h^2)\)。

我们先考虑一个完整的矩形如何计算答案：对于一个 \(n\times m\) 的矩形，要放 \(k\) 个，那么显然答案就是

\[\binom{n}{k}\times \binom{m}{k}\times k! \]

然后我们考虑把这个直方图拆成若干个矩形，分别计算答案再进行合并。这里借一张图：

图源：https://www.luogu.com.cn/blog/Marser/solution-p6453

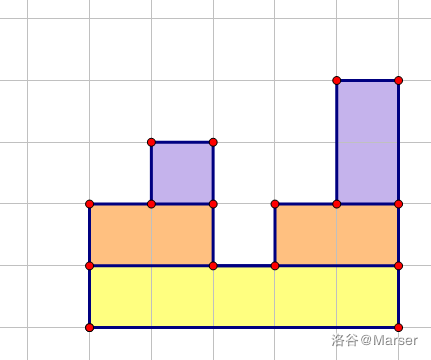
对于笛卡尔树上的一个节点 \(u\)，我们先合并出来两个儿子的背包状态，再枚举最下面选了多少个，如果上面选了 \(k\) 个，下面要放 \(x\) 个，那么方案数就是 \(C_{\text{L}(u)-k}^{x}\times C_{h_u}^x\times x!\)。AC Code

Luogu4689 Ynoi2016 这是我自己的发明 Present 7.5

首先我们可以以 \(1\) 为根求个 \(\text{DFS}\) 序，那么设当前根为 \(r\)，若 \(r\) 不在 \(x\) 的子树内，那么 \(x\) 子树所代表的区间就是 \([\text{DFN}(x),\text{DFN}(x)+\text{size}(x)-1]\)；否则我们找到 \(x\to r\) 路径上的第一个节点 \(y\)，那么区间就是 \([1,n]-[\text{DFN}(y),\text{DFN}(y)+\text{size}(y)-1]\)。

第二种可以倍长一下序列转化为一个区间。然后现在相当于要对两个区间 \([l_1,r_1],[l_2,r_2]\) 计算答案。

我们考虑差分，转化为

\[[1,r_1]\times [1,r_2]-[1,l_1-1]\times [1,r_2]-[1,r_1]\times [1,l_2-1]+[1,l_1-1]\times [1,l_2-1] \]

然后现在相当于有 \(4m\) 个询问，每次问 \([1,x]\) 和 \([1,y]\) 中随便选两个点，颜色相等的情况数。

我们发现可以直接用莫队做，于是这题就做完了。。

吐槽一下，lxl 课件上面说会拆出来 5e6 个询问还要基排之类的东西，然而实际上倍长序列就只需要 2e6 个了。。

AC Code

CF453B Little Pony and Harmony Chest Present 7.0

给定一个长度为 \(N\) 的序列 \(A\)，求一个序列 \(B\) 使得 \(\sum |A_i-B_i|\) 最小。

要求 \(B\) 中任意两个元素都互质。\(1\le N\le 100,1\le A_i\le 30\)。

首先我们可以直接摆烂把 \(B_i\) 取成 \(1\)。这意味着 \(B_i\) 不可能超过 \(59\)。

\(1\sim 59\) 中有 \(17\) 个质数，考虑直接状压：\(f(i,S)\) 表示前 \(i\) 个数只用 \(S\) 内的质因子的最小代价，转移随便做。

复杂度大概是 \(2^{17}\times n\times 60\)，看上去貌似过不去。

但实际上我们需要访问到的状态远远不到这么多，常数非常非常小，写个记忆化就无压力 AC 了。

AC Code