2022.7.26 做题记录

CF1702G Passable Paths Present 4

题目大意是给定一棵 \(n\) 个节点的树与 \(q\) 组询问，第 \(i\) 次给出 \(k_i\) 个点，问这些点是否在一条链上。

\(1\le n,q\le 2\times 10^5,1\le \sum k_i\le 2\times 10^5\)。

建个虚树然后随便判断一下就行了

考虑动态加入点，不断维护当前链的两个端点。加入一个点时只需判断该点是否在当前的链上。

复杂度 \(O(n+(q+\sum k)\log n)\)。AC Code

CF1707C DFS Trees Future 7.5

挺妙的题。独立做出来了一个 *2400，好耶

• 由于边权不同，最小生成树实际上是唯一的。
• 因此，考虑一条非树边 \((u,v)\)，观察样例一，一开始我猜测这代表 \(u\to v\) 路径上不包括端点的所有点都会走歪，得不到真正的 MST。
• 证明很简单：考虑路径上的一个点 \(x\)，不妨设 \(x\) 第一步会朝 \(u\) 的方向走（注意 MST 唯一，因此只要走错一步就意味着 \(x\) 不符合要求，故可行的路径其实是唯一的），那么想要回到 \(v\)，必然要经过 \((u,v)\)，选取这条不优的边。因为在 DFS 的过程中我们不会走回头路。
• 但样例二是一个反例。

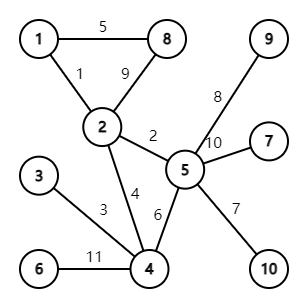
图中的 \(8\) 号点也会走歪，但它不满足上面的要求。

经过一些思考可以得到正确的结论：

• 对于一个点 \(r\)，若 MST 以 \(r\) 为根时图中不存在横叉边，那么 \(r\) 是合法的。也就是说，若以 \(r\) 为根是，任意非树边 \((u,v)\) 总是满足 \(u,v\) 中的一个是另一个的祖先，那么 \(r\) 是符合要求的。
• 充分性显然。必要性也不难证明：如果 \(u,v\) 是一条横叉边，设 \(z=\text{LCA}(u,v)\)，若 \(r\) 在走向 \(z\) 的过程中已经走歪了显然不行；否则 \(r\) 在走到 \(z\) 后就变成了上面讨论的情况，必然会走向一边然后歪掉 \((u,v)\) 这条边。

因此现在只需要算出来以每个点为根时是否存在横叉边。

我们先随便提一个根出来，设 \(S_u\) 表示 \(u\) 子树内所有节点的集合，对于一条路径 \((u,v)\)：

• 若 \(u,v\) 互不为对方的祖先，那么所有在 \(S_{\text{root}}-S_u-S_v\) 中的节点均不符合要求。
• 否则，不妨设 \(u\) 是 \(v\) 的祖先，设 \(x\) 是 \(v\) 的 \(\text{dep}_v-\text{dep}_u-1\) 级祖先（即 \(u\) 的某个直接儿子，同时也是 \(v\) 的祖先），那么所有在 \(S_x-S_v\) 中的节点均不符合要求。

于是现在相当要给一个子树做一个覆盖之类的东西。可以直接拍平成 \(\text{DFS}\) 序转成序列问题差分解决。

算上求 \(k\) 级祖先/并查集之类的东西，时间复杂度不超过 \(O(n\log n)\)。AC Code